样本数据的初步分析方法

一、数值分析

初步描述样本的分布：顺序统计量 分位数 均值 中位数 样本方差

近似密度函数：

 

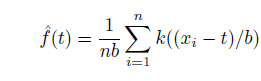
近似累积分布函数：

 

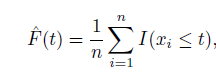
对于多个变量，通过协方差矩阵、相关系数矩阵反映变量之间的相关性

 

二、图形初步分析

直方图——密度图，盒形图

QQ图：反映两个变量之间的分布相似程度，变量和某一个分布之间的契合程度，越接近一条斜率为1的直线，越相似。可以用来初步检验样本数据是否满足某个分布。

 

三、数据变换

一般情况下，尽量不要盲目对原数据进行变换（容易丧失其原本的数据内部信息）。

某些特殊情形下，例如若数据偏度过大从而使得不利于后续分析，可以适当进行数据转换。

例如：使用线性回归时，残差可能不符合正态分布从而不满足建模条件，则可以对响应变量Y进行变换，把数据变成正态的，一定程度上减少残差和预测变量的相关性。

 

Box-Cox变换：

 

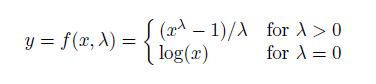
 lambda的取值选择：

lambda<1时，取值较小的部分被拉伸，取值较大的部分被压缩，lambda>1时则相反。

所以应当首先判断数据的偏斜情况，如果是左偏，则可以去lambda=0 or <1，若是右偏，可以取lambda>1。