2025春《机器学习导论》课程笔记（一~二）：引言、监督学习

目录

• Lec 1 引言
  • 机器学习
  • 监督学习与无监督学习
  • 基本术语
  • 发展历程
• Lec 2 监督学习
  • 定义
  • 损失函数
  • 泛化
  • 训练与测试
  • 小结

Lec 1 引言

机器学习

• 人工智能的一个分支，关注设计和开发算法以使计算机能够根据经验数据来不断改进其行为。
• 假设用 \(P\) 来评估计算机程序在某任务类 \(T\) 上的性能，若一个程序通过利用经验 \(E\) 在 \(T\) 中任务上获得了性能改善，则我们就说关于 \(T\) 和 \(P\)，该程序对 \(E\) 进行了学习。

监督学习与无监督学习

• 监督学习 (supervised learning) 是一种算法，它从一个训练数据集中学习。我们知道正确的答案或期望的输出，算法利用给定的数据集进行预测，并由 supervisor（监督者）进行纠正。当算法达到可接受的性能水平时，学习过程停止。

• 无监督学习 (unsupervised learning) 正如其名，没有训练者或监督者；我们不展示输出，或者达到特定输出所需的特定输入。

基本术语

针对数据：

• 数据集（dataset）\(D\) 与样本
• 属性（attribute）或特征（feature）\(x\)
• 标签（label）\(y\)
• 训练/学习
• 训练集与测试集

针对任务：

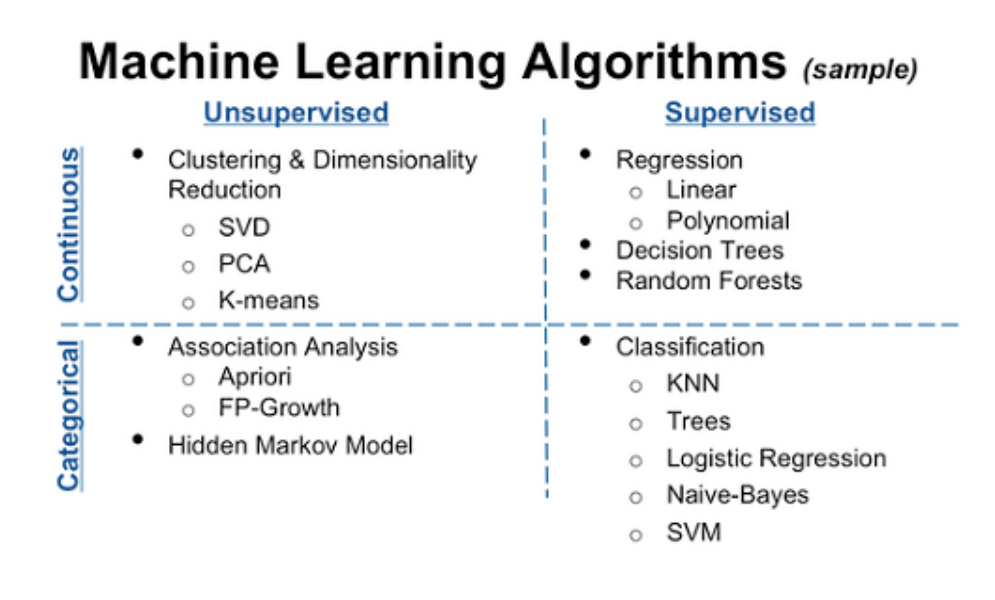
• 分类 (Classification)：离散值
• 回归 (Regression)：连续值
• 聚类 (Clustering): 无标记信息，对数据分组
• 降维 (Dimension Reduction): 无标记信息，对数据降维

有无标记信息：

• 监督学习 (Supervised learning)：提供预期的正确输出（有标记数据）
• 无监督学习 (Unsupervised learning)：仅提供无标记数据
  半监督学习 (Semi-supervised learning) ：同时使用有标记数据和无标记数据
  自监督学习 (Self supervised learning)：自学成才。无监督学习的特例，自动生成标签用于训练

基本术语：

• 样本空间和特征向量
• 独立同分布(independent and identically distributed，i.i.d.)
• 泛化 (Generalization) 能力
• 假设空间 (Hypothesis)（目标：在模型空间中搜索不违背训练集的假设）
• 归纳偏好：如 “奥卡姆剃刀”(Occam’s razor)原则，“若有多个假设与观察一致，选最简单的那个”。

基本定理：

• 没有免费的午餐 (No Free Lunch，NFL) 定理：在考虑所有可能的问题和算法的情况下，所有算法的性能都是一样的，即没有一种算法能在所有问题上都表现最好。不存在一种“放之四海而皆准”的最优算法。

• 概率近似正确 (Probably Approximately Correct，PAC) 定理：
  \(P(|f(x)−y|≤ϵ) ≥ 1−δ\)
  学习算法能够以高概率在一个接近正确的程度上输出正确的假设（模型），即模型的输出大概率是近似正确的。

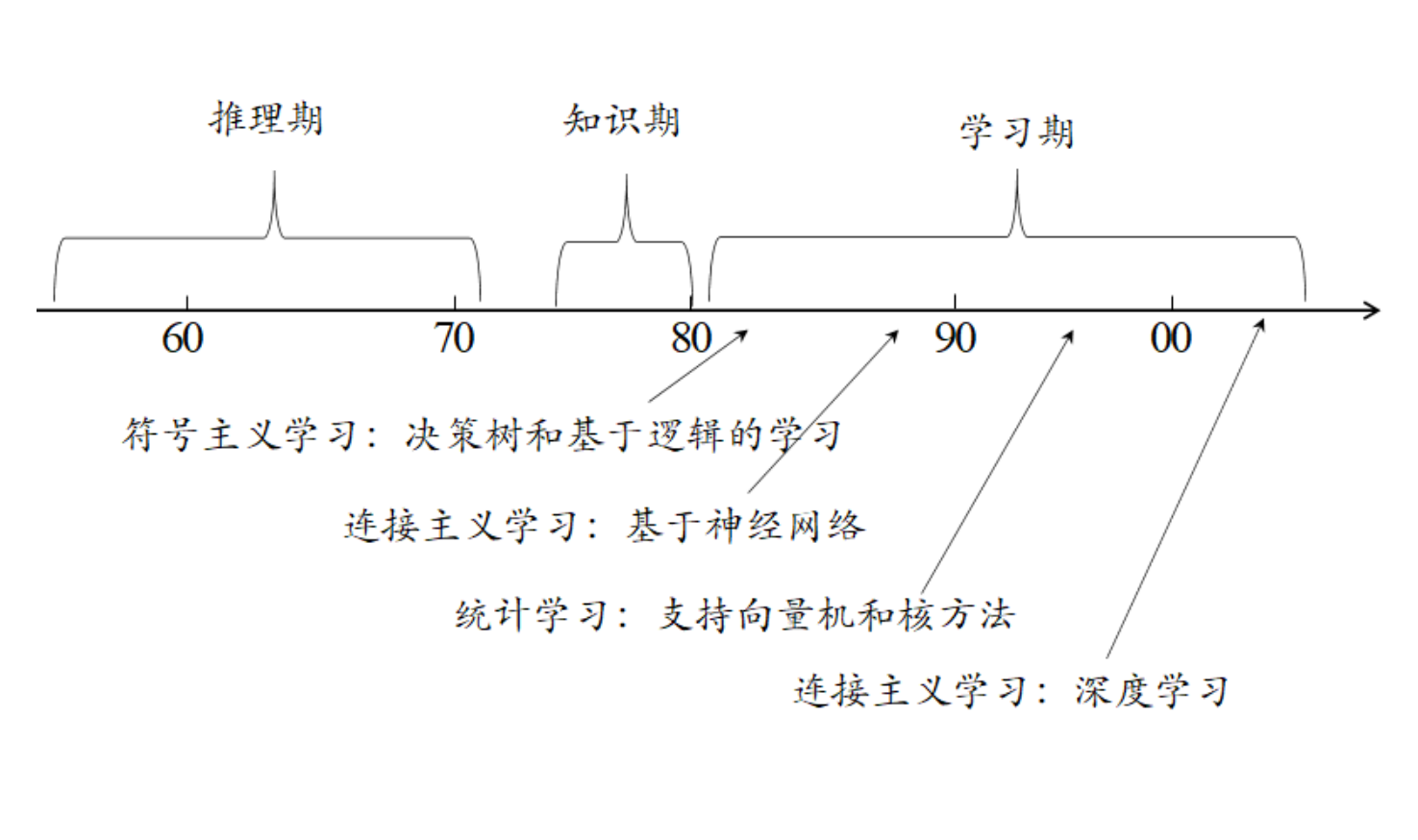
发展历程

Lec 2 监督学习

定义

机器学习的数据集由输入对 \((x, y)\) 来表示，其中 \(x ∈ R^d\) 表示输入数据，\(y\) 表示对应的分类标签。整个训练数据集的表示形式如下：

\(D =\left \{ (x_1, y_1), ..., (x_n, y_n) \right \} ⊆ R^d × C\)

其中：

\(R^d\) 表示 \(d\) 维特征空间 (d-dimensional feature space)
\(x_i\) 表示第 \(i\) 个样本 (sample) 的输入向量
\(y_i\) 表示第 \(i\) 个样本的标签 (label)
\(C\) 表示数据集的标签空间

数据点 \((x_i, y_i)\) 服从某个未知的分布 \(P(X, Y)\)。我们希望通过学习，最终可以找到一个函数 \(h\)，对于新的输入数据 \((x, y)\) ∼ \(P\)，有比较高的置信度满足 \(h(x) = y\) (或者 \(h(x) ≈ y\))。

损失函数

损失函数（Loss Functions）是一种评估算法对数据集建模效果的方法。

如果预测完全错误，损失函数将输出一个较大的值。如果预测很好，它将输出一个较小的值。当改变算法的一部分，试图改进模型时，损失函数会告诉你这是否有效。

0-1 损失（Zero-one loss）

\(\mathcal{L} _{0/1}(h) = \frac{1}{n} \sum_{i=1}^{n}{\delta_{h(x_i) \ne y_i}}, \quad where\,{\delta_{h(x_i) \ne y_i}}=\left\{\begin{matrix}1, \quad {h(x_i) \ne y_i} \\0,\quad \quad \quad \, \, o.w.\end{matrix}\right.\)

该损失函数返回数据集 D 上的错误率。0-1 的损失对每个错误分类的点施加相同的惩罚，因此“错误离谱”的点 (即边界点)不会受到太多关注，这在直观上是不适宜的。0-1 损失为不连续和非凸的，优化的难度较大。

均方损失（Squared loss）

\(\mathcal{L} _{sq}(h) = \frac{1}{n} \sum_{i=1}^{n}{({h(x_i) - y_i})^2}\)

通常用于回归。均方损失函数有两个效果: 损失值总是非负; 损失值与误差的绝对值呈平方增长关系。
缺点: 如果一个预测非常接近正确，如 \(|h(x_i) − y_i| = 0.001\)，平方将是微小的，很少会注意到这个示例 (example)，以获得零误差。

绝对值损失（Absolute Loss）

\(\mathcal{L} _{abs}(h) = \frac{1}{n} \sum_{i=1}^{n}{|{h(x_i) - y_i}|}\)

通常用于回归。损失与错误预测呈线性增长，更适合于有噪声的数据 (当一些错误预测是不可避免的，不应该主导损失)。如果给定一个输入 \(x\)，标签 \(y\) 是概率分布 \(P(y|x)\)，那么将绝对损失最小化的最佳预测是预测中值，即 \(h(x) = medianP(y|x)[y]\)。

泛化

泛化（Generalization）
给定一个损失函数，我们可以尝试找到使损失最小化的函数 \(h = argmin_{h∈H} \mathcal L(h)\)。机器学习的很大一部分内容都集中在这个问题上，即如何有效地最小化，使它对不在 D 中的示例，仍然能得到正确的结果。

反例：死记硬背型，穷举型，死记硬背 + 乱猜型，...。

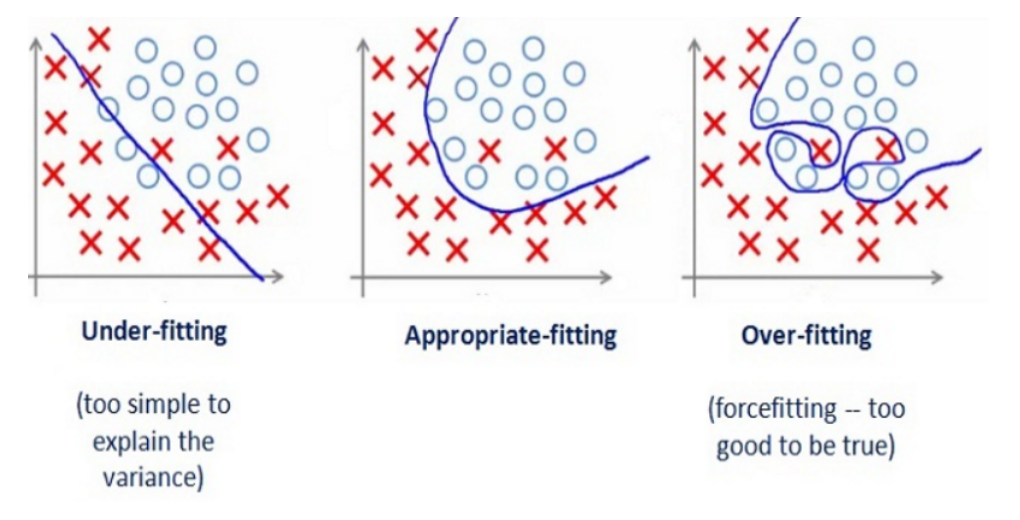
过拟合: 学习器把训练样本本身特点当做所有潜在样本都会具有的一般性质。
欠拟合: 训练样本的一般性质尚未被学习器学好。

训练与测试

根据没有免费的午餐定理(No free lunch rule)：训练集和测试集来自同一个分布；需要做一些假设 (Assumptions) 或偏好 (Bias)。

通常将 \(D\) 分成三个子集: \(D_{TR}\) 为训练数据，\(D_{VA}\) 为验证数据，\(D_{TE}\) 为测试数据。通常它们被分成 80%、10% 和 10% 的比例。

为什么我们需要 \(D_{VA}\)?
\(D_{VA}\) 用于检查从 \(D_{TR}\) 获得的 \(h(·)\) 是否存在过拟合问题。\(h(·)\) 将需要在 DVA 上验证，如果损失太大，\(h(·)\) 将根据 \(D_{TR}\) 进行修改，并在 \(D_{VA}\) 上再次验证。这个过程将反复执行，直到它在 \(D_{mathmVA}\) 损失足够小。\(D_{TR}\) 和 \(D_{VA}\) 的大小之间的权衡: 较大的 \(D_{TR}\) 的训练结果会更好，但如果 \(D_{VA}\) 更大，验证将更可靠 (噪音更小)。

分割数据：

分割依据。按时间划分/均匀随机（当 (且通常仅当) 数据为独立同分布（i.i.d.）时采用均匀随机）。绝对不要按字母顺序或特征值分割！用测试误差/测试损失近似真实的泛化误差/泛化损失。

分割方式。

• 留出法
• 交叉验证法（将数据集分层采样划分为 \(k\) 个大小相似的互斥子集，每次用 \(k-1\) 个子集的并集作为训练集，余下的子集作为测试集，最终返回 \(k\) 个测试结果的均值，\(k\) 最常用的取值是 \(10\)。）
• 自助法（对数据集 \(D\) 有放回采样 \(m\) 次得到训练集 \(D′\)，剩余的作为测试集。在数据集较小、难以有效划分训练/测试集时很有用）

混淆矩阵
混淆矩阵的列代表模型预测的标签，行表示样本实际的标签。二分类时候，如果将正预测记作 \(P\)，负预测记作 \(N\)，分别对应于样本的实际标签予以逻辑判断正确 \(T\) 和错误 \(F\)，可以生成 \(TP\),\(FP\),\(TN\),\(FN\) 四个标签。混淆矩阵有助于研究者观察模型预测各类别的能力，并据此分析潜在的可能原因和模型性能提升方法。

	正预测	负预测
正样本	\(TP\)	\(FN\)
负样本	\(FP\)	\(TN\)

查准率 \(P\)(precision) 与查全率 \(R\)(recall)

查准：宁可漏网，不可错选。 \(P=\frac {TP} {TP+FP}\)

查全：宁可错选，不可漏网。 \(R=\frac {TP} {TP+FN}\)

小结