小仙女儿的强化学习笔记（零）马尔科夫过程

马尔科夫过程 Markov Process

---

1.1马尔科夫性 Markov Property

　　马尔科夫决性定义为：在一个随机过程中，给定现在状态和所有历史状态，其未来状态的条件概率分布只依赖于当前状态，与历史状态是条件独立的。简单来说，即下一时刻的状态只与当前状态有关，与历史状态无关(一个渣男下一刻会不会爱你只取决于这一刻对你的新鲜感，而与之前的感情无关😊)。

可以用下面的状态转移概率公式来描述马尔科夫性（在离散状态下）：

\[{P_{ss'}} = P\left[ {{S_{t + t}} = s'|{S_t} = s} \right]\]

        所有的状态转移概率可由矩阵表示：

\[P = from\mathop {\left[ {\begin{array}{*{20}{c}}
{{P_{11}}}& \cdots &{{P_{1n}}}\\
\vdots &{}& \vdots \\
{{P_{n1}}}& \cdots &{{P_{nn}}}
\end{array}} \right]}\limits^{to} \]

1.2马尔科夫过程 Markov Process

　　满足马尔科夫性的随机过程即为马尔科夫过程，马尔科夫链（Markov chain）是最简单的马氏过程，即时间和状态过程的取值参数都是离散的马氏过程。马尔科夫链可由元组<S,P>表示，其中S是有限数量的状态集，P是状态转移概率矩阵。

　　示例，一个简单的马尔科夫链：

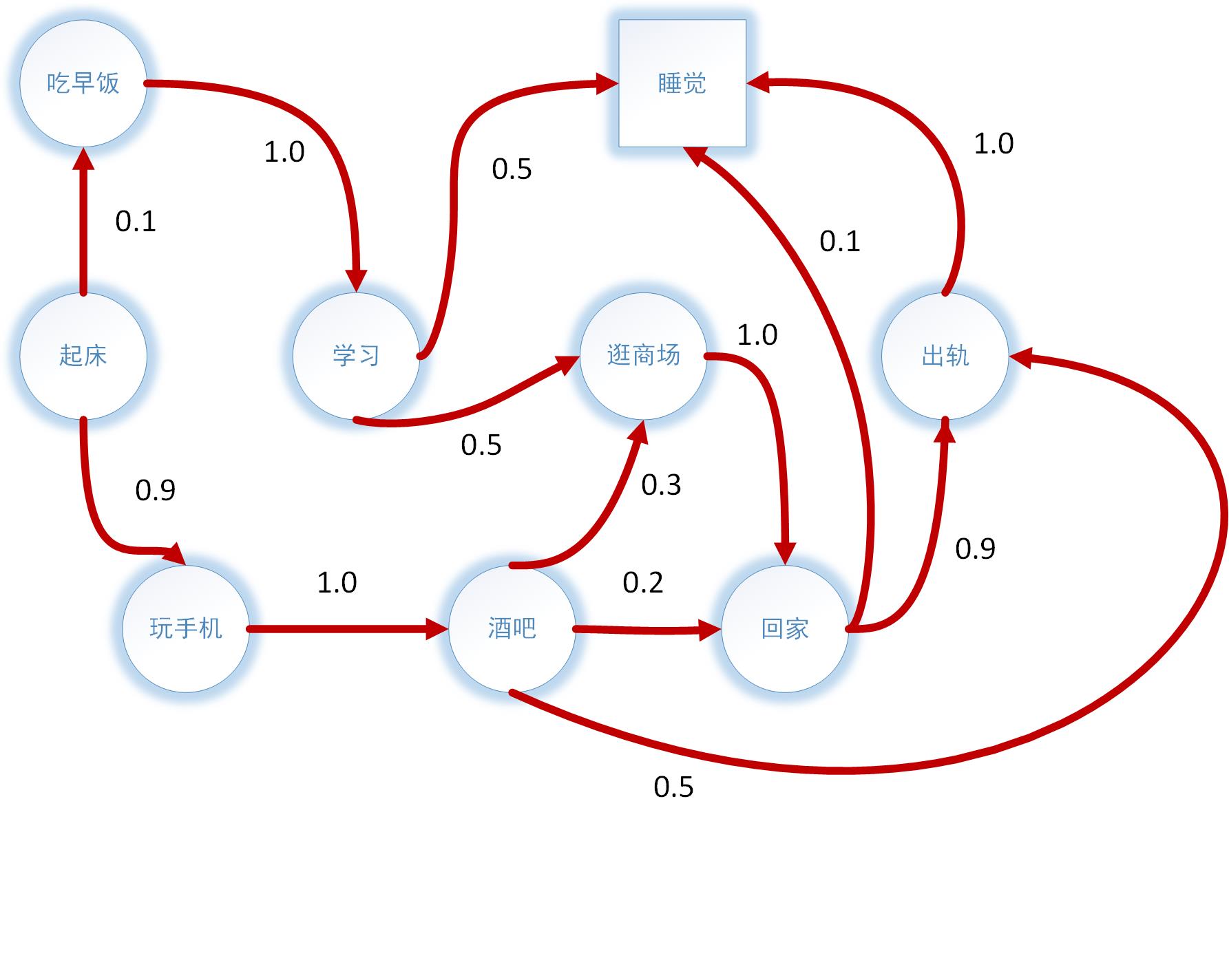
　　起床为起始状态，睡觉为终止状态，每个完整的过程都称作为Sample Episodes，例如以下过程都是一个可能的episode：

　　起床→吃早饭→学习→睡觉

　　起床→玩手机→酒吧→回家→出轨→睡觉

　　该马尔科夫过程的状态转移矩阵为：

\[P = \begin{array}{*{20}{c}}
{}&\vline& {wakeup}&{breakfast}&{phone}&{study}&{pub}&{shopping}&{home}&{affair}&{sleep}\\
\hline
{wakeup}&\vline& {}&{0.1}&{0.9}&{}&{}&{}&{}&{}&{}\\
{breakfast}&\vline& {}&{}&{}&{1.0}&{}&{}&{}&{}&{}\\
{phone}&\vline& {}&{}&{}&{}&{1.0}&{}&{}&{}&{}\\
{study}&\vline& {}&{}&{}&{}&{}&{0.5}&{}&{}&{0.5}\\
{pub}&\vline& {}&{}&{}&{}&{}&{0.3}&{0.2}&{0.5}&{}\\
{shopping}&\vline& {}&{}&{}&{}&{}&{}&{1.0}&{}&{}\\
{home}&\vline& {}&{}&{}&{}&{}&{}&{}&{0.9}&{0.1}\\
{affair}&\vline& {}&{}&{}&{}&{}&{}&{}&{}&{1.0}\\
{sleep}&\vline& {}&{}&{}&{}&{}&{}&{}&{}&{1.0}
\end{array}\]

　　状态转移矩阵可以理解为有权重的单向网络图，可以计算出每个状态可能发生的概率。

1.3马尔科夫奖励过程 Markov Reward Process

　　马尔科夫奖励过程是在马尔科夫的基础上增加了奖励R和衰减系数γ，由元组表示为<S,P,R,γ>。S状态下t+1时刻所能获得的奖励，是前一时刻t在状态s下所能得到的奖励期望，是一个确定值：

\[{R_s} = {\rm{E}}\left[ {{R_{t + 1}}|{S_t} = s} \right]\]

　　可以理解为在某一状态结束后才获得相对应的奖励，可以修改为：

\[{R_s} = {\rm{E}}\left[ {{R_t}|{S_t} = s} \right]\]

　　即在进入某一状态时即获得当前状态奖励。

　　如图即为马尔科夫奖励过程，每种状态有相应的奖励值。

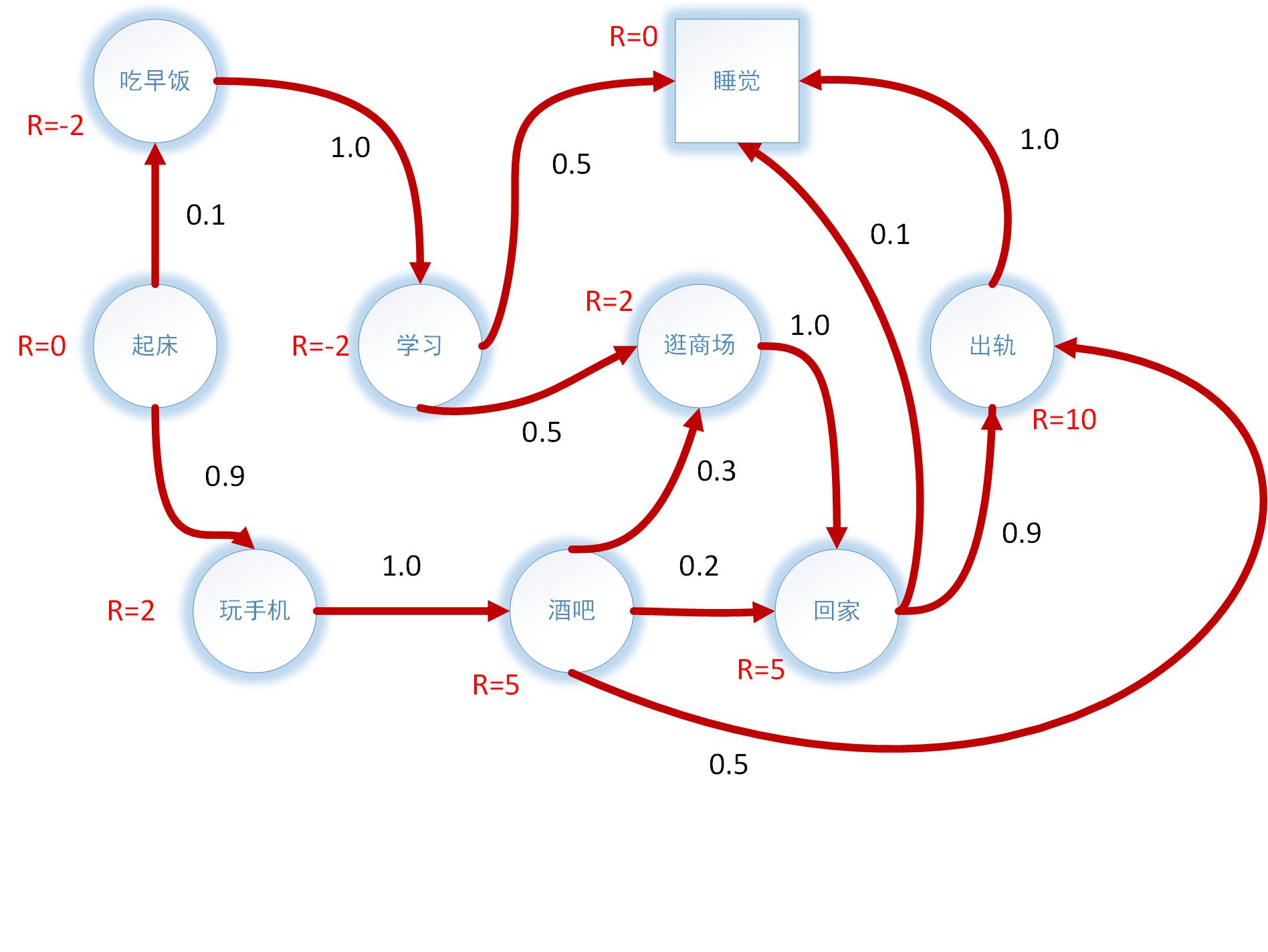
收获Return

　　收获定义为一个马尔科夫链上从t时刻开始往后所有的奖励乘以衰减系数Discount Factor的总和，公式如下：

\[{G_t} = {R_{t + 1}} + \gamma {R_{t + 2}} +  \ldots  = \sum\limits_{k = 0}^\infty  {{\gamma ^k}{R_{t + k + 1}}} \]

　　衰减系数γ体现了未来的奖励在当前时刻的价值比例，且γ越小并且距离当前状态越远，对当前状态价值的影响越小。

　　约定进入某一状态时即收获当前奖励，则公式修改为：

\[{G_t} = {R_t} + \gamma {R_{t + 1}} +  \ldots  = \sum\limits_{k = 0}^\infty  {{\gamma ^k}{R_{t + k}}} \]

价值函数Value Function

　　在不引入动作之前，价值函数是描述一个状态价值的大小，一个马尔科夫奖励过程中某一状态的价值函数是从该状态开始的马尔科夫链收获的期望：

\[{v_\pi }\left( s \right) = {{\rm{E}}_\pi }\left[ {{G_t}|{S_t} = s} \right]\]

　　举例，假设γ值为0.5，求“起床”状态的价值：

　　起床-吃早饭-学习-睡觉

\[G = 0*{\left( {\frac{1}{2}} \right)^0} + \left( {{\rm{ - }}2} \right)*{\left( {\frac{1}{2}} \right)^1} + \left( {{\rm{ - }}2} \right)*{\left( {\frac{1}{2}} \right)^2} + \left( 0 \right)*{\left( {\frac{1}{2}} \right)^3}\]

　　起床-玩手机-酒吧-回家-睡觉

\[G = 0*{\left( {\frac{1}{2}} \right)^0} + \left( 2 \right)*{\left( {\frac{1}{2}} \right)^1} + \left( 5 \right)*{\left( {\frac{1}{2}} \right)^2} + \left( 5 \right)*{\left( {\frac{1}{2}} \right)^3}{\rm{ + }}\left( 0 \right)*{\left( {\frac{1}{2}} \right)^4}\]

　　需要说明的是，在这里并不是一个状态的所有价值，只是该状态在一个episode中的价值。

贝尔曼方程Bellman Function

　　既然在马尔科夫过程中，当前状态与历史状态无关，根据状态价值函数可以推导出：

\[\begin{array}{l}
v\left( s \right) = {\rm{E}}\left[ {{G_t}|{S_t} = s} \right]\\
\;\;\;\;\;\;\; = {\rm{E}}\left[ {{R_t} + \gamma {R_{t + 1}} + \ldots |{S_t} = s} \right]\\
\;\;\;\;\;\;\; = {\rm{E}}\left[ {{R_t} + \gamma {G_{t + 1}}|{S_t} = s} \right]\\
\;\;\;\;\;\;\; = {\rm{E}}\left[ {{R_t} + \gamma v(s + 1)|{S_t} = s} \right]
\end{array}\]

　　推导出的公式即为贝尔曼方程，一个常数的期望还是其本身，因此可以写为：

\[v\left( s \right) = {R_s} + \gamma {\rm{E}}\left[ {v(s + 1)|{S_t} = s} \right]\]

　　该方程由两部分组成，前部分表示该状态的即时奖励期望，就是该状态的即时奖励R_t；后半部分是下一状态的价值期望与衰减系数的乘积。如果已知状态之间的转移概率，用s’表示s状态下一时刻所有可能到达的状态，贝尔曼方程可表示为：

\[v\left( s \right) = {R_s} + \gamma \sum\limits_{s' \in S} {{P_{ss'}}} v\left( {s'} \right)\]

　　所有状态的贝尔曼方程就可以组成一个方程组，通过线性代数中的表述方式可以写成：

\[\left[ {\begin{array}{*{20}{c}}
{v\left( 1 \right)}\\
\vdots \\
{v\left( n \right)}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{R_1}}\\
\vdots \\
{{R_n}}
\end{array}} \right] + \gamma \left[ {\begin{array}{*{20}{c}}
{{P_{11}}}& \cdots &{{P_{1n}}}\\
\vdots &{}& \vdots \\
{{P_{n1}}}& \cdots &{{P_{nn}}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{v\left( 1 \right)}\\
\vdots \\
{v\left( n \right)}
\end{array}} \right]\]

　　v是一组变量，R是一组常数项，P是状态转移概率矩阵，前文中已经给出，因此这是一个线性方程组，可以直接解析法求解或者用迭代法求解，迭代法就是雅各比迭代或者高斯赛德尔迭代。

　　举例，初始化所有状态价值均为0，γ值为0.5，求“回家”和“酒吧”状态的价值：

　　回家   \[v\left( {home} \right) = 5 + 0.5*\left( {0.9{\rm{*}}v\left( {affair} \right) + 0.1{\rm{*}}v\left( {sleep} \right)} \right) = 5\]

　　酒吧   \[v\left( {pub} \right) = 5 + 0.5*\left( {0.3{\rm{*}}v\left( {shopping} \right) + 0.2{\rm{*}}v\left( {home} \right) + 0.2{\rm{*}}v\left( {affair} \right)} \right) = 5\]

　　在求完所有状态的价值之后，得到的结果作为下一次迭代的初始值，不断地循环迭代，最后收敛后的结果即为状态的真实价值。试想，在一次迭代过程中，能否将某一状态求出来的结果作为接下来状态求解的初始值？即将“回家”状态的值5带入到求解“酒吧”的方程之中，求解出来的结果为5.5，从而加快收敛速度？可以，这种求解思想即为高斯赛德尔迭代法。  

1.4马尔科夫决策过程 Markov Decision Process

　　在马尔科夫奖励过程的基础上再加入动作空间A即为马尔科夫决策过程，元组表示为<S,A,P,R,γ>。在这里，状态转移概率P和奖励R不再只是对一个状态来说，而是与一个状态s以及动作a相对应，公式为：

\[P_{ss'}^a = P\left[ {{S_{t + t}} = s'|{S_t} = s,{A_t} = a} \right]\]

\[R_s^a = {\rm{E}}\left[ {{R_t}|{S_t} = s,{A_t} = a} \right]\]

策略Policy

　　既然有了动作空间，那在不同的状态下如何选择动作？这就是由策略π所决定的，π(a|s)表示马尔科夫过程中某一状态下动作a可能被选择的概率，完整表达式为：

\[\pi \left( {a|s} \right) = {\rm{P}}\left[ {{A_t} = a|{S_t} = s} \right]\]

　　通常可选择的策略有随机策略，即所有动作被选择的概率是一样的；或者ε-soft策略，1-ε的概率选择最优策略，以ε的概率随机选取动作。

　　在一个马尔科夫决策过程中，执行策略π时，状态s转移到状态s’总的概率由每个动作可能被选择的概率与该动作能使状态s转移到s’的概率的乘积最后累加成和得到，公式为：

\[P_{ss'}^\pi  = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} P_{ss'}^a\]

　　而奖励函数可以认为。在执行策略π时，状态s得到的即时奖励是该状态该策略下所有可能动作得到的奖励与该动作发生的概率的乘积的和，但通常情况下是一样的，即在同一状态下不同动作得到的奖励都是一样的（能否不同动作设置不同奖励？），公式如下：

\[R_s^\pi  = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} R_s^a\]

动作价值函数Action-value Function

　　如前所述价值函数是状态价值函数，在基于策略π的情况下，公式改写为：

\[{v_\pi }\left( s \right) = {{\rm{E}}_\pi }\left[ {{G_t}|{S_t} = s} \right]\]

　　表示在执行策略π时，状态s所得到的的奖励期望。

　　动作价值函数q，表示在执行策略π时，状态s下执行动作a所能得到的奖励期望，行为价值函数实际上应是行为动作价值函数，它所对应的是一个动作价值对，公式如下：

\[{q_\pi }\left( {s,a} \right) = {{\rm{E}}_\pi }\left[ {{G_t}|{S_t} = s,{A_t} = a} \right]\]

　　根据定义我们对马尔科夫链进行修改，将状态节点“酒吧”改为两个动作，一个是“走路去酒吧”，一个是“开车去酒吧”，我们假定使用随机策略，即这两个动作被选择的概率是一样的，而这两个动作使状态转变的概率不一样，假定“开车去酒吧”导致回家的可能概率更大。从例子中我们可以看出，不同动作可以指向同一状态，事实上，不同状态也可以选择同一动作，例如走格子都可以选择上下左右，但动作价值函数告诉我们只有动作和状态相对应的时候价值才有意义，换言之，不同状态下的相同动作是独立的，而不同动作导致的相同状态则是一样的，价值是累加的。

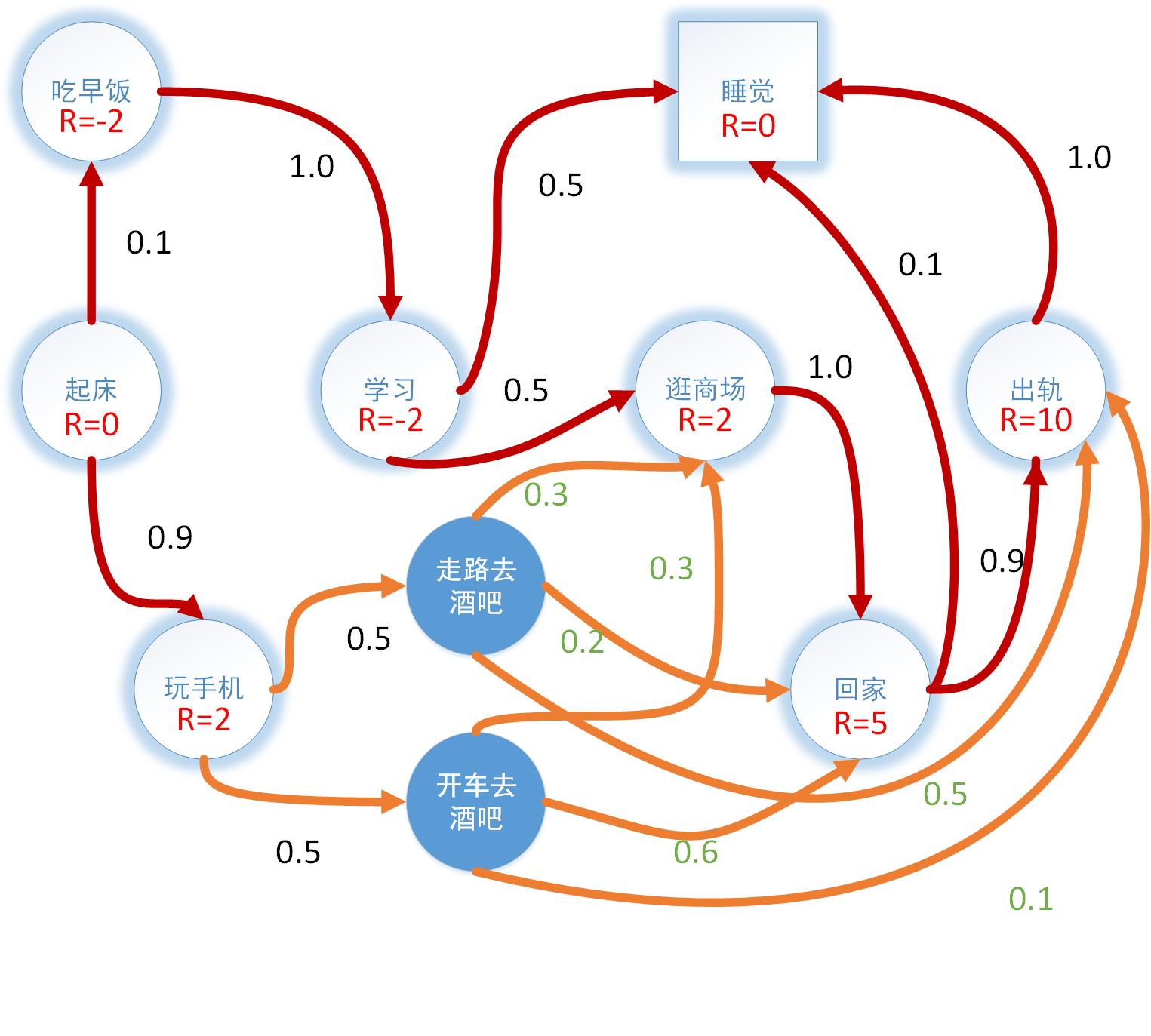
　　用树形结构可以更清楚的表示：

　　从上图中可知状态价值函数v与动作价值函数q的关系为：

\[{v_\pi }\left( s \right) = R_s^{} + \sum\limits_{a \in A} {\pi \left( {a|s} \right)} {q_\pi }\left( {s,a} \right)\]

　　同样动作价值函数q与状态价值函数v的关系为：

\[{q_\pi }\left( {s,a} \right) = \gamma \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)\]

　　将下式带入上式可以推导出：

\[{v_\pi }\left( s \right) = R_s^{} + \gamma \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)\]

　　同样将上式带入下式可以推导出：

\[{q_\pi }\left( {s,a} \right) = \gamma \sum\limits_{s' \in S} {P_{ss'}^a} \left( {R_s^{} + \sum\limits_{a' \in A} {\pi \left( {a'|s'} \right)} {q_\pi }\left( {s',a'} \right)} \right)\]

　　举例，依旧初始化所有状态价值均为0，γ值为0.5，求“玩手机”状态的价值：

\[v\left( {phone} \right) = 2 + 0.5*0.5*\left( \begin{array}{l}
0.2*v\left( {home} \right) + \\
0.3*v\left( {shopping} \right) + \\
0.5*v\left( {affair} \right)
\end{array} \right) + 0.5*0.5*\left( \begin{array}{l}
0.6*v\left( {home} \right) + \\
0.3*v\left( {shopping} \right) + \\
0.1*v\left( {affair} \right)
\end{array} \right) = 2\]

　　如假定在离开状态s时获得奖励R，则上述四公式为：

\[{v_\pi }\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} {q_\pi }\left( {s,a} \right)\]

\[{q_\pi }\left( {s,a} \right) = R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)\]

\[{v_\pi }\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)} \right)\]

\[{q_\pi }\left( {s,a} \right) = R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a} \left( {\sum\limits_{a' \in A} {\pi \left( {a'|s'} \right)} {q_\pi }\left( {s',a'} \right)} \right)\]

　　假定同一状态下不同动作得到的奖励都是一样的且与状态相对应则：

\[\begin{array}{l}
{v_\pi }\left( s \right) = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \left( {R_s^a + \gamma \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)} \right)\\
\;\;\;\;\;\;\;\;\; = \sum\limits_{a \in A} {\pi \left( {a|s} \right)} R_s^a + \gamma \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)\\
\;\;\;\;\;\;\;\;\; = {R_s} + \gamma \sum\limits_{a \in A} {\pi \left( {a|s} \right)} \sum\limits_{s' \in S} {P_{ss'}^a} {v_\pi }\left( {s'} \right)
\end{array}\]

　　举例，将上图中状态改为动作，每一动作仅对应一个状态，例如吃早饭作为一个动作，1的概率转移到吃早饭这个状态，起床状态下可选择的动作为吃早饭、玩手机，概率均为0.5。初始化所有状态为0，γ值为0.5，随机策略，迭代三次结果为：

起床	早饭	手机	学习	回家	商场	出轨	睡觉
0	0	0	0	0	0	0	0

起床	早饭	手机	学习	回家	商场	出轨	睡觉
0	-2	2	-2	5	2	10	0

起床	早饭	手机	学习	回家	商场	出轨	睡觉
0	-2.75	4.8	-1.5	7.5	4.5	10	0

　　从表中可以看出收敛趋势，计算过程中可以发现，末状态作为中止状态，价值是不会变得，因此如果从中止状态反推可以得到所有的状态价值，实际上可以对方程组直接求解。

最优价值函数Optimal Value Function

　　从所有策略产生的状态价值函数，选取使状态s价值最大的函数：

\[{v_*} = \mathop {\max }\limits_\pi  {v_\pi }\left( s \right)\]

　　最优动作价值函数：

\[{q_*}\left( {s,a} \right) = \mathop {\max }\limits_\pi  {q_\pi }\left( {s,a} \right)\]

　　通过最大化最优动作价值函数得到最优策略：

\[{\pi _*}\left( {a|s} \right) = \left\{ {\begin{array}{*{20}{c}}
1&{if\;a = \mathop {\arg \max }\limits_{a \in A} {q_*}\left( {s,a} \right)}\\
0&{otherwise}
\end{array}} \right.\]

贝尔曼最优方程Bellman Optimality Equation

　　一个状态的最优价值等于该状态所采用的所有动作产生的行为价值中最大的那个行为价值并加上当前状态的奖励：

\[{v_*} = {R_s}\mathop { + \max }\limits_a {q_*}\left( {s,a} \right)\]

　　一个动作的最优价值是该动作所能达到的所有状态与概率的乘积的求和：

\[{q_*}\left( {s,a} \right) = \gamma \sum\limits_{s' \in S} {P_{ss'}^a} {v_*}\left( {s'} \right)\]

　　将下式带入上式可以得到v的推导公式：

\[{v_*} = {R_s}\mathop { + \gamma \max }\limits_a \sum\limits_{s' \in S} {P_{ss'}^a} {v_*}\left( {s'} \right)\]

　　将上式带入下式可以得到q的推导公式：

\[{q_*}\left( {s,a} \right) = \gamma {R_{s'}} + \mathop {\max }\limits_a \sum\limits_{s' \in S} {P_{ss'}^a} {q_*}\left( {s',a} \right)\]

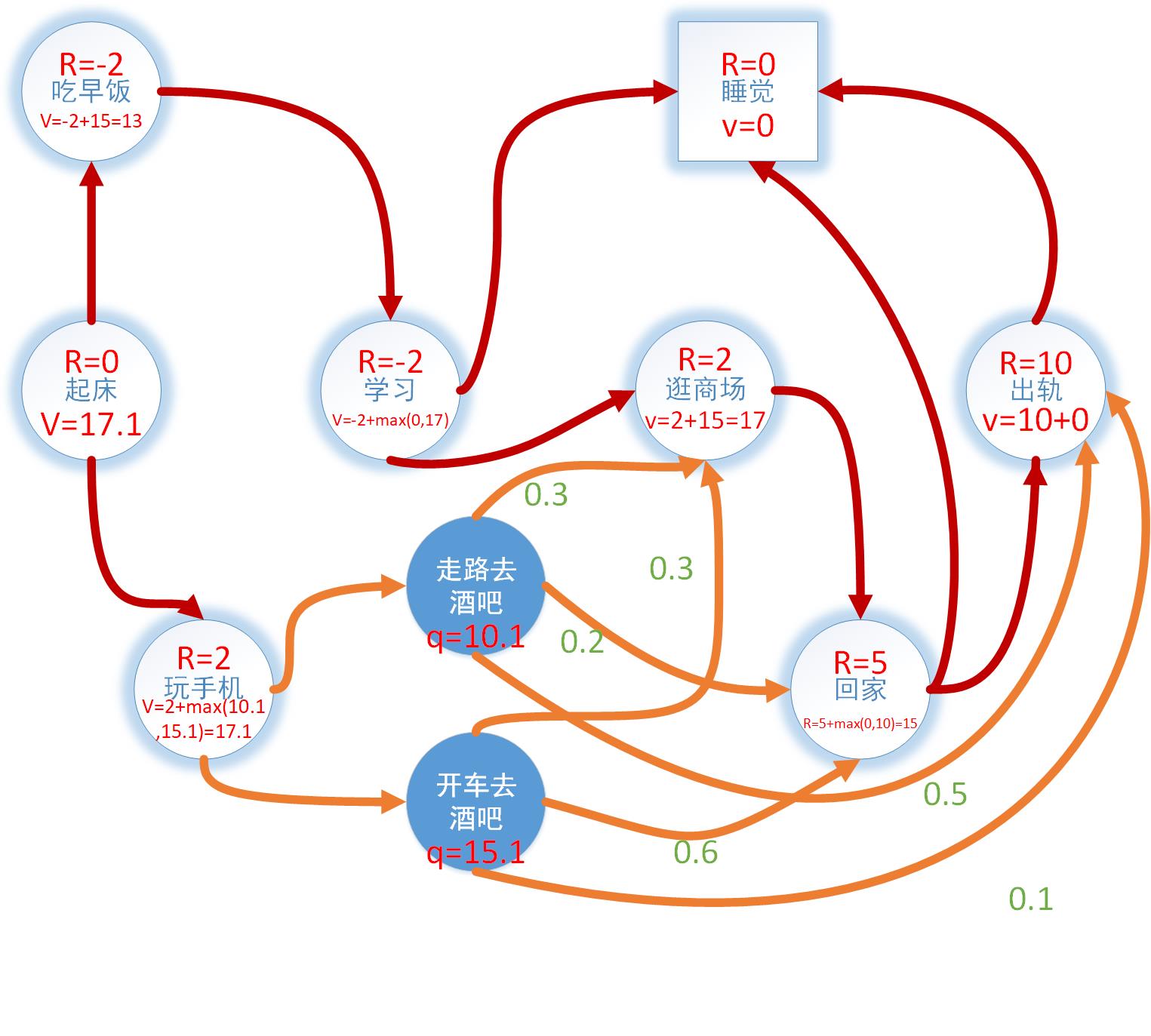
　　举例，为计算方便，γ值设为1。最终结果如图所示，最优策略：

　　起床-玩手机-开车去酒吧-回家-出轨-睡觉

　　事实上选取不同的γ值，得到的结果并不一样。

 

什么呀\[\hat{\beta_0}\]