【攻防世界】SECCON-CTF-2014 - Decrypt-It-easy
附件给了个可执行文件和一个加密文件，还给了个readme告诉你加密文件就是用可执行文件加密的
可执行文件逆出来是这样的：
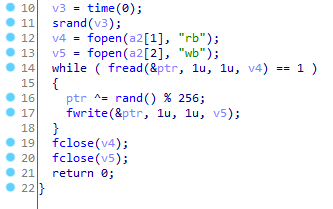
是的，输入一个文件，给每个字节异或一个随机数再输出来……
由于加密的是png，前8位是固定文件头，那或许可以破解伪随机数
很自然的想法是爆破，但是时间戳太大了，枚举时间比较长
不过这里使用时间戳加密，因此可以灵稽一动，想到从这场比赛举办的时间附近开始枚举
比赛在2014年举办，那么从2014/01/01的时间戳开始枚举，结果还真的枚举到了囧
（需要注意一点，Linux上的gcc和Windows上的gcc编译完的程序使用相同种子似乎会得到不同的伪随机数，附件里的可执行文件是Linux平台的，因此爆破脚本也应该跑在Linux上）
解完之后是一张图片，这个图片才是真正意义上的密码学题
加密的柿子很简单，但是我没找到什么优美的办法，只能直接配方，然后pq拆成两个柿子，然后二次剩余，然后再中国剩余定理拼回来囧
这里需要注意一点，二次剩余是有重根的，因此对于解出来的m1和m2，还要分别枚举4种情况，找出最有可能是flag的解密串输出（一般判断有没有不可见字符就行了）
代码：
1 from random import randint 2 from Crypto.Util.number import * 3 from gmpy2 import * 4 5 6 def exgcd(a, b): 7 if b == 0: 8 return 1, 0 9 x, y = exgcd(b, a % b) 10 return y, x - a // b * y 11 12 13 def crt(a, m): 14 M = 1 15 for i in m: 16 M = M * i 17 18 ans = 0 19 for i in range(len(a)): 20 x, y = exgcd(M // m[i], m[i]) 21 ans = (ans + a[i] * M // m[i] * x) % M 22 23 return (ans + M) % M 24 25 26 def mul_i(a, b, t, p): 27 return [(a[0] * b[0] + a[1] * b[1] * t) % p, (a[0] * b[1] + b[0] * a[1]) % p] 28 29 30 def pow_i(a, b, c, t, p): 31 ans = [1, 0] 32 z = [a, b] 33 while c > 0: 34 if c % 2 == 1: 35 ans = mul_i(ans, z, t, p) 36 z = mul_i(z, z, t, p) 37 c = c // 2 38 39 return ans 40 41 42 def legendre(a, p): 43 return pow(a, (p - 1) // 2, p) 44 45 46 def residue(n, p): 47 t = randint(0, p - 1) 48 while legendre(t ** 2 - n, p) != p - 1: 49 t = randint(0, p - 1) 50 51 a = pow_i(t, 1, (p + 1) // 2, t ** 2 - n, p) 52 # print('residue:', a[0] * a[0] % p == n) 53 return a[0] 54 55 56 def get_string(m): 57 s = '' 58 while m > 0: 59 s = s + chr(m % 256) 60 m = m // 256 61 62 return s[::-1] 63 64 65 def check_visible(s): 66 for i in s: 67 if not 32 <= ord(i) < 128: 68 return 0 69 70 return 1 71 72 73 if __name__ == '__main__': 74 ''' 75 n = 0xB8AE199365 76 b = 0xFFEEE 77 c = 0x8D5051562B 78 ''' 79 N = [0xB8AE199365, 0xB86E78C811, 0x7BD4071E55] 80 B = [0xFFEEE, 0xFFFEE, 0xFEFEF] 81 C = [0x8D5051562B, 0x5FFA0AC1A2, 0x6008DDF867] 82 t = '' 83 for i in range(len(N)): 84 n = N[i] 85 b = B[i] 86 c = C[i] 87 p = 1 88 for i in range(2, n): 89 if n % i == 0: 90 p = i 91 q = n // i 92 break 93 94 b2 = b * invert(2, p) % p 95 r1 = residue((c + b2 * b2) % p, p) 96 m1 = [(r1 - b2 + p) % p, (p - r1 - b2 + p) % p] 97 b2 = b * invert(2, q) % q 98 r2 = residue((c + b2 * b2) % q, q) 99 m2 = [(r2 - b2 + q) % q, (q - r2 - b2 + q) % q] 100 for temp1 in m1: 101 for temp2 in m2: 102 m = crt([temp1, temp2], [p, q]) 103 s = get_string(m) 104 if check_visible(s): 105 break 106 107 # print('crt1:', m % p == m1) 108 # print('crt2:', m % q == m2) 109 110 # print(s[::-1]) 111 t = t + s 112 113 print(t)
更新：
在我看了攻防世界admin题解之后，才终于明白怎么用中国剩余定理优雅地做这道题
n很小，qp更小，直接在[0,p)和[0,q)枚举m，就能得到m = m1 (mod p)和m = m2 (mod q)
然后中国剩余定理拼一下就vans了
