【C# 数据结构】树 开篇
学习路径
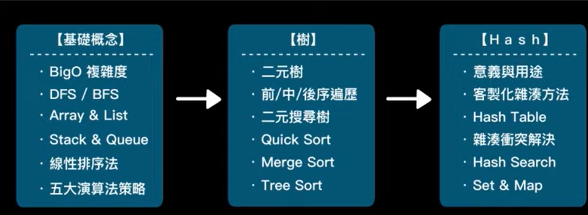
然后去leetcode刷简单的题目。
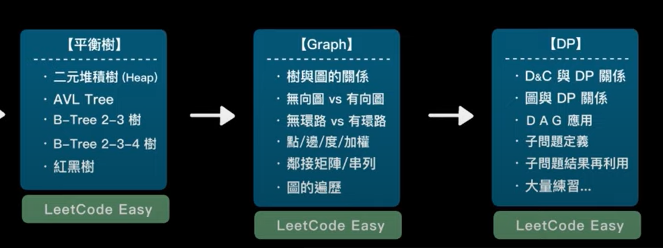
然后去leetcode刷简单的题目。
复习所有 在刷leetcode难部分
树的定义
树可以用递归的形式来定义:树T是由n(n>=0)个结点组成的有限集合,他或者是颗空树,或者包含一个根结点和零或若干棵互不相干的子树。
可以使用广义表(纯表)的形式树结构,如下树结构用广义表表示:A(B(E,F),C(G),D(H,I,J))
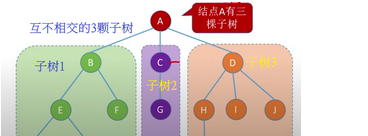
表示树结构的广义表没有共享和递归成分,是一种纯表。广义表中的原子对应于树的叶节点,树的非叶子结点则用子表结构表示。
空树:节点树为0的树,即n=0时,称为空树。
非空树:一颗非空树T具有以下特点
(1)有且仅有一个根节点
(2)没有后继的节点称为“叶子节点”,有后继的节点称为“分子节点”.
(3)当树的结点数n>1时,根结点之外的其他结点可以分为m(m>=1)个互不相交的集合T1,T2,T3.。。。Tm,其中每个集合Ti(1<=i<=m)具有与树T相同的树结构,称为子树。每颗子树的根结点有且仅有一个直接的前驱结点。
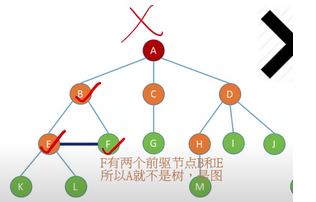
这是图
树的分类:
树结构可以分为有序和无序树两种类型,有序树种最常用的是二叉树。
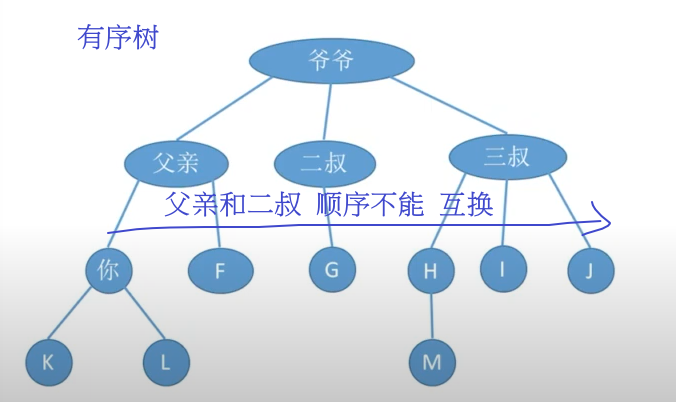
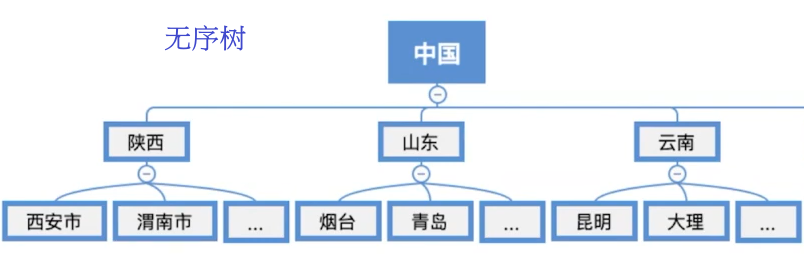
树结构的应用场景:
操作系统的文件系统,根目录是文件树的根节点,子目录是树中的分子节点,文件是树结构的叶子节点。
除了根节点外,任何节点有且仅有一个前驱,有多个前驱的节点的叫图。叶子节点没用后继节点。
森林
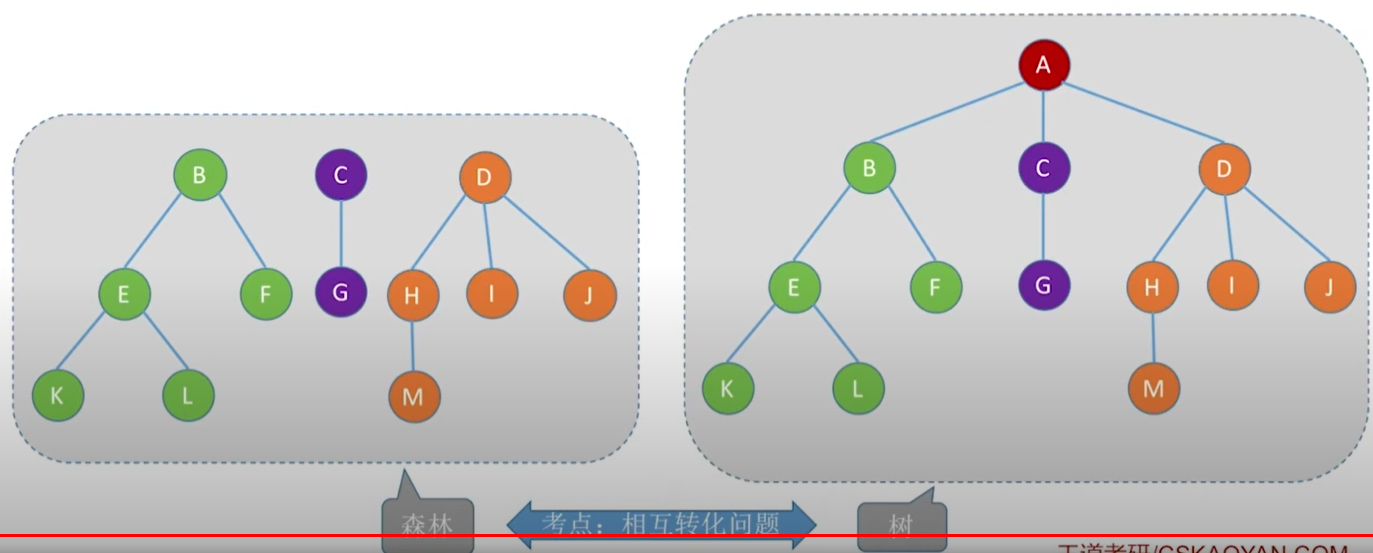
若干颗互不相交的树的集合称为森林。给森林加上一个根节点就变成一颗树。将树的根结点删除就变成由子树组成的森林。
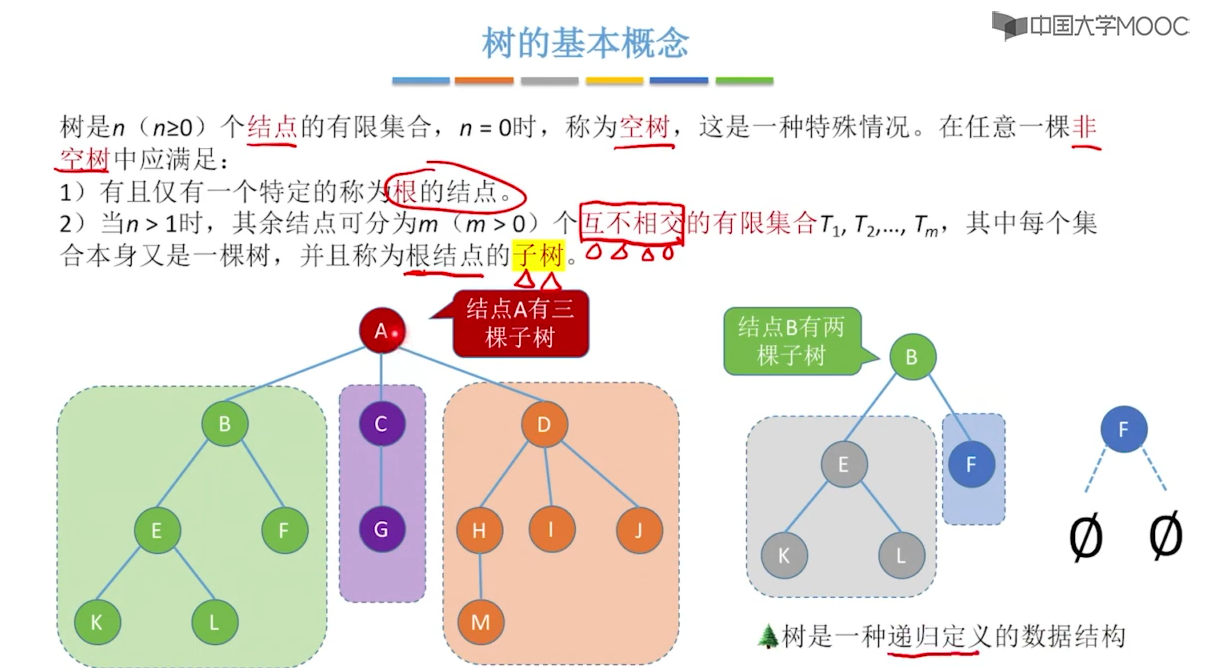
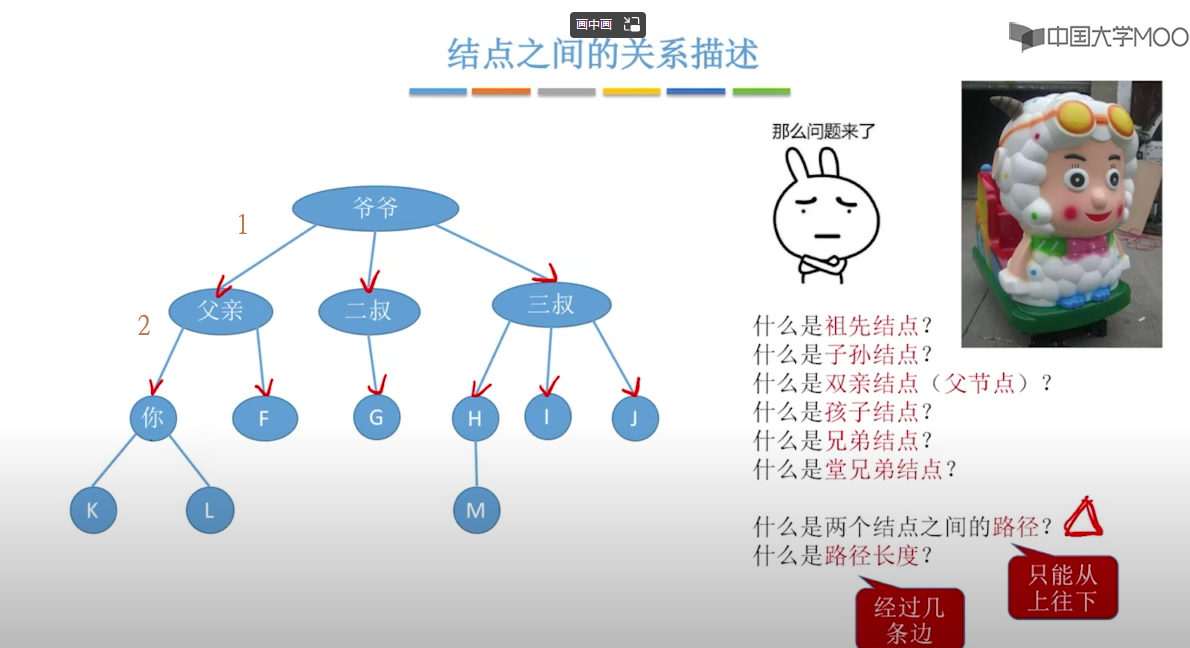
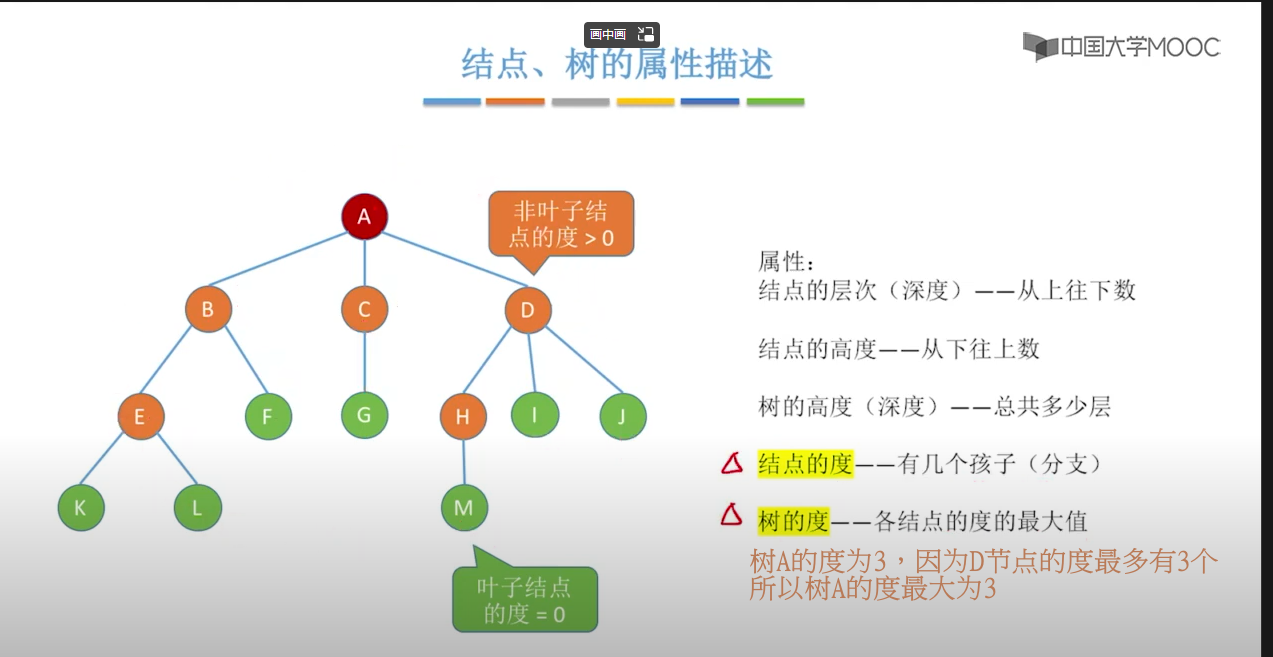
C# 节点的深度是从0开始计算的。
树类型概述:
二叉树,完全二叉树,满二叉树,二叉排序树,平衡二叉树,红黑树,B树,B+树,B*树、2-3-4树、2-3树
平衡二叉树开始涉及到旋转。
操作
二叉树常用操作旋转(rotate),该操作为常数时间复杂度。 二叉树旋转前后,中序遍历的结果不变。因此树的任何部分旋转,对整棵树的元素顺序没有影响。
在哈夫曼树中用到。
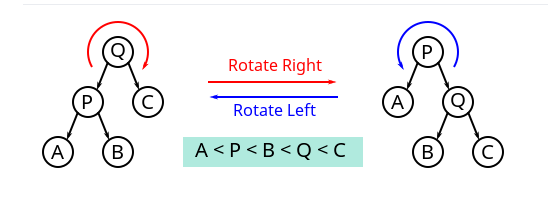
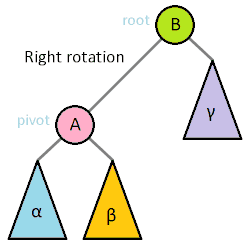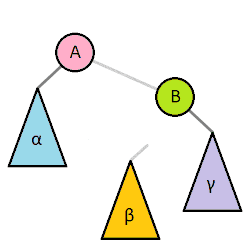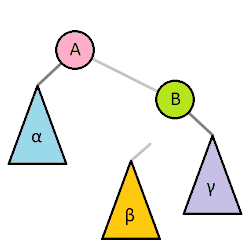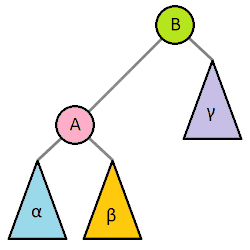
总结
为什么有了数组和链表还要引入二叉树?
针对数组和链表的优缺点,无法说链表一定优于数组,或者是数组一定优于链表,因为某些长期的需要,所以就推出一个相对折中的二叉树。
为什么有了二叉树还要引入平衡二叉树?
有了二叉树还不算完,二叉树有一种极端的情况,就是所有的子结点偏向一端,二叉树退化成链表,这就相当于我选择了这种的二叉树,你现在罢工不干了,找了个链表来糊弄我...
所以为了解决二叉查找树退化为链表的情况,引入了平衡二叉树,即:
平衡二叉树是为了解决二叉树退化成一棵链表而诞生的。
既然有了平衡二叉树,这下总没有问题了吧?
为什么有了平衡二叉树还要引入红黑树?
但是是实际使用过程中,因为平衡二叉树追求绝对严格的平衡关系,显然这个规则在于频繁的插入、删除等操作的情景性能肯定会出现问题...
所以为了解决这个问题,进而又引入了红黑树。
平衡二叉树追求绝对严格的平衡,平衡条件必须满足左右子树高度差不超过1,红黑树是放弃追求完全平衡,它的旋转次数少,插入最多两次旋转,删除最多三次旋转,所以对于搜索、插入、删除操作较多的情况下,红黑树的效率是优于平衡二叉树的。
红黑树是终结吗?
时代总是进步的,大胆猜测不会是,就跟当初从数组、链表到二叉树一样。
至此,通过这篇希望大家对整个树结构的出现有一个基础的概念,目前面试中最为常问的就是红黑树了,当然这得益于 HashMap,但红黑树还有挺多其他的知识点可以考察,例如红黑树有哪些应用场景?红黑树与哈希表在不同应该场景的选择?红黑树有哪些性质?红黑树各种操作(插入删除查询)的时间复杂度是多少?等等等等...
树的双亲表示法、孩子表示法和孩子兄弟表示法
在使用树结构描述实际问题时,大多数不是二叉树,更多的是普通的树结构,在存储之间具有普通树结构的数据时,经常使用的方法有3种:
双亲表示法
取一块连续的内存空间,在存储每个结点的同时,各自都附加一个记录其父结点位置的变量。
代码表示:
- #define tree_size 100//宏定义树中结点的最大数量
- #define TElemType int//宏定义树结构中数据类型
- typedef struct PTNode{
- TElemType data;//树中结点的数据类型
- int parent;//结点的父结点在数组中的位置下标
- }PTNode;
- typedef struct {
- PTNode nodes[tree_size];//存放树中所有结点
- int r,n;//根的位置下标和结点数
- }PTree;
例如,使用双亲表示法存储图 1(A)中的树结构时,数组存储结果为(B):
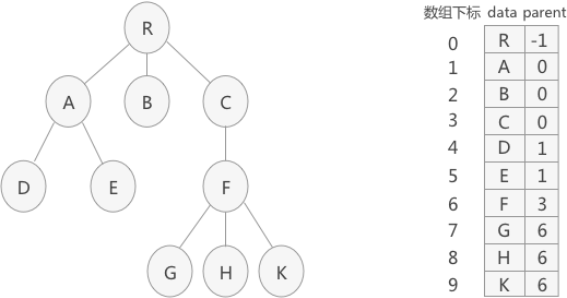
(A) (B)
图 1 双亲表示法
当算法中需要在树结构中频繁地查找某结点的父结点时,使用双亲表示法最合适。当频繁地访问结点的孩子结点时,双亲表示法就很麻烦,采用孩子表示法就很简单。
孩子表示法
将树中的每个结点的孩子结点排列成一个线性表,用链表存储起来。对于含有 n 个结点的树来说,就会有 n 个单链表,将 n 个单链表的头指针存储在一个线性表中,这样的表示方法就是孩子表示法。
如果结点没有孩子(例如叶子结点),那么它的单链表为空表。
代码表示:
- #define TElemType int
- #define Tree_Size 100
- //孩子表示法
- typedef struct CTNode{
- int child;//链表中每个结点存储的不是数据本身,而是数据在数组中存储的位置下标
- struct CTNode * next;
- }*ChildPtr;
- typedef struct {
- TElemType data;//结点的数据类型
- ChildPtr firstchild;//孩子链表的头指针
- }CTBox;
- typedef struct{
- CTBox nodes[Tree_Size];//存储结点的数组
- int n,r;//结点数量和树根的位置
- }CTree;
例如,使用孩子表示法存储图 1 (A),存储效果如图 2:
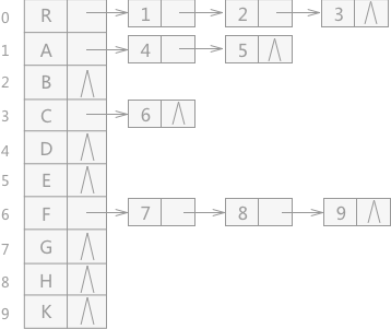
图 2 孩子表示法
使用孩子表示法存储的树结构,正好和双亲表示法相反,适用于查找某结点的孩子结点,不适用于查找其父结点。可以将两种表示方法合二为一,存储效果如图 3:
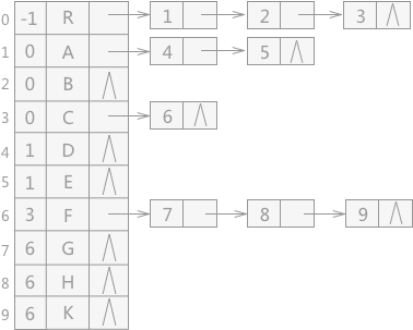
图 3 孩子双亲表示法
孩子兄弟表示法
使用链式存储结构存储普通树。链表中每个结点由 3 部分组成:

图 4 结点构成
其中孩子指针域,表示指向当前结点的第一个孩子结点,兄弟结点表示指向当前结点的下一个兄弟结点。
代码表示:
- #define ElemType int
- typedef struct CSNode{
- ElemType data;
- struct CSNode * firstchild,*nextsibling;
- }CSNode,*CSTree;
通过孩子兄弟表示法,普通树转化为了二叉树,所以孩子兄弟表示法又被称为“二叉树表示法”或者“二叉链表表示法”。
例如,用孩子兄弟表示法表示图 1 (A)的普通树,存储结果为:
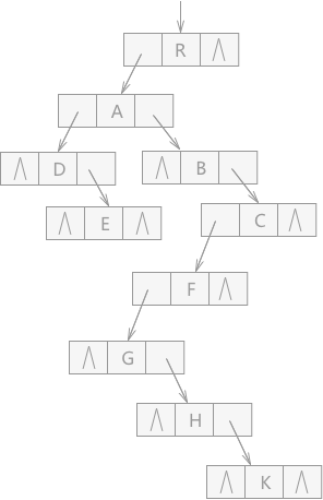
图 5 二叉链表表示法
补:森林和二叉树的相互转化
通过孩子兄弟表示法的学习,对于任意一棵树,都可以找到唯一的一棵二叉树与之对应。
普通树转化成的二叉树,其根结点都没有右孩子,即普通树对应的二叉树肯定没有右子树。
而森林是由多棵树组成,为了便于对森林的遍历等操作,需要将森林中的所有树都组合成一颗大的二叉树,转化步骤为:
- 首先将森林中树各自转化为二叉树;
- 森林中第一棵二叉树的树根作为转化后二叉树的树根;
- 其他树的树根作为第一棵树树根的兄弟结点,进行连接;
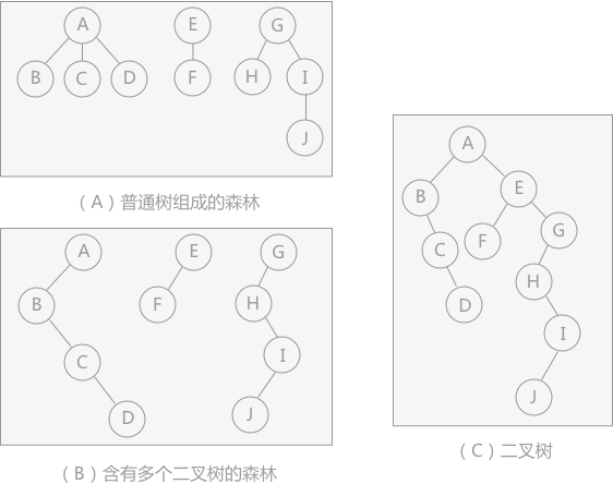
图 6 森林转化成二叉树
如图 6 所示,(A)中由三棵普通树组成的森林,首先三棵普通树采用孩子兄弟表示法各自转化成二叉树,如(B)所示;然后由(B)转(C)时,将森林中第一棵树的树根作为转化后的整棵二叉树的树根,其他数的树根作为第一棵树的树根的兄弟结点,如(C)所示。
转化成二叉树的森林,做的最多的操作就是查找树中的结点。在遍历转化后的二叉树时,遍历方式有先序遍历、中序遍历和后序遍历。
B C D A F E H J I G。总结
树的三种表示方法中,双亲表示法和孩子表示法在实际算法中的应用场景正好相反:双亲表示法应用于解决查找某结点的父结点,而孩子表示法应用于查找某结点的孩子结点。
孩子兄弟表示法可以将普通树转化成二叉树存储,在实际操作中,可以应用二叉树的性质来解决普通树或者森林的问题。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号