位运算的奇“赢”技巧

大家好啊，我是小慕，好久不见，甚是想念，今天让我们一起学习位运算的相关知识，一起刷怪升级吧！

 

一、什么是位运算？

        程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算说穿了，就是直接对整数在内存中的二进制位进行操作。每左移一位就相当于是对该数乘以2， 每右移一位就相当于是对该数除以2。     是不是太简单了啊,哈哈

 

二、常见的7种位运算

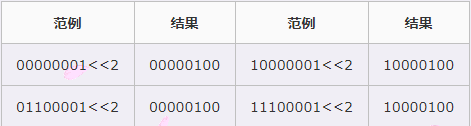
①左移（<<）

左移运算是将操作数二进制值逐位左移若干位，左移过程中符号位不变，高位溢出则舍弃，低位则补0。

 

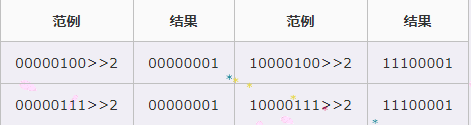
②右移（>>）

右移运算是将操作数二进制值逐位右移若干位，右移过程中符号位不变，低位溢出则舍弃，并用符号位补溢出的高位，即负数补1，正数补0。

 

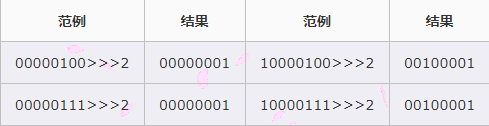
③无符号右移（>>>）

无符号右移运算是将操作数所有二进制值逐位右移若干位，包括最高位符号位，也跟着右移，低位溢出并舍弃，高位补0。要注意的是，无符号右移（>>>）中的符号位（最高位）也会跟着变。

 

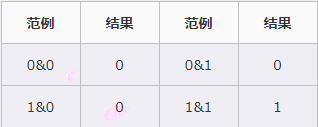
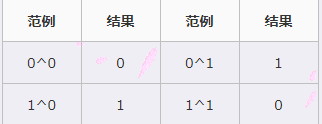
④与（&）

与运算是将参与运算的两个二进制数进行&运算，如果两个二进制位都是1，则与运算的结果为1，其他全部都是0。

 

⑤或（|）

或运算是将参与运算的两个二进制数进行|运算，如果两个二进制位都是0，则与运算的结果就是0，其他全都是1。即只要其中一个数字的二进制位是1，这个二进制位的运算结果就是1。要注意的是，符号位也是同样的操作。

 

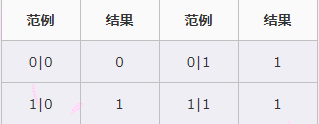
⑥非（~）

非运算符也叫做取反运算符，只针对一个二进制数进行操作，如果二进制位是0，则取反位1；如果二进制位是1，则取反位0。要注意的是，符号位也是同样的操作。

 

⑦异或（^）

异或运算符是将参与运算的两个二进制数进行异或运算，如果两个二进制位相同，则结果为1，否则为0。

 

三、位运算的常见使用套路

 

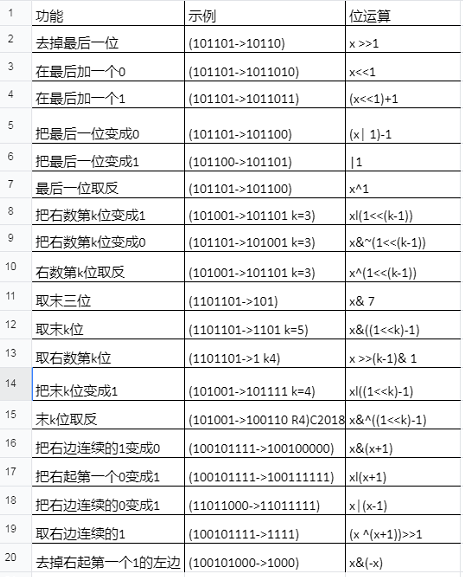
小慕建议把这些套路先背下来，熟练生巧呀！

 

 

 

四、位运算的实战案例

 

关卡1、找出只出现一次的数

在一个数组中有一个数只出现了一次，其他数都出现了两次，找出这个只出现了一次的数。

 

哈希表解法： 

用一个哈希表存储该数组，每次存储的时候，记录 某个数出现的次数，最后再遍历哈希表，看看哪个数只出现了一次。这种方法的时间复杂度为 O(n)，空间复杂度也为 O(n)。

 

位运算解法：一个数和 0 异或的结果是它本身，所以我们把这一个数组全部异或一下，异或支持交换律和结合律。也就是说，那些出现了两次的数异或之后会变成0，那个出现一次的数，和 0 异或之后就等于它本身。（时间复杂度为 O(n)，空间复杂度为 O(1)，太棒了！）

int find(int[] arr){    int tmp = arr[0];    for(int i = 1;i < arr.length; i++){        tmp = tmp ^ arr[i];    }    return tmp;}

 

关卡2、如何求m的n次方，且不能使用库函数pow()。

（这下把你们难住了吧，O(∩_∩)O哈哈~，厉害的大佬们在旁边喊   “难？就这？”这也叫难？）

 

位运算解法：

例如 n = 13，则 n 的二进制表示为 1101, 那么 m 的 13 次方可以拆解为:m^1101 = m^0001 * m^0100 * m^1000

我们可以通过 & 1和 >>1 来逐位读取  1101里的二进制位，为1时将该位代表的乘数累乘到最终结果。  时间复杂度近为 O(logn)。

代码如下：(关注点：在while循环中，无论走不走if，temp始终以自乘的速度扩增，然后对n一边右移，一边判断n的末位二进制是不是1)

int myPow(int n){    int sum = 1;    int tmp = m;    while(n != 0){        if(n & 1 == 1){             sum *= tmp;        }        tmp *= tmp;        n = n >> 1;    }    return sum;}

好啦，以上的两个个小题是不是都学会啦，答：我学会了。
 今天的内容到此结束，我们下期再见，爱你们的小慕

 

半山腰总是最挤的，你得去山顶上瞅瞅，拜拜

好，今天的内容就分享到这里了，你们一定要变优秀哦，我们下期再见。

现在公众号迁移到这个啦， 不要迷路了，慕仔们，加油哦！

       接下来的一段时间，我会专注Java技术栈，计算机网络，数据结构和算法，操作系统，设计模式，计算机组成原理，数据库原理，设计模式来做分享，欢迎你们和我一起学习，一起提高，Fighting!