剑指Offer

一、二分法

二、链表

No14、 链表中倒数第k个结点

方法一：暴力解法；

方法二：使用如图的快慢指针，首先让快指针先行k步，然后让快慢指针每次同行一步，直到快指针指向空节点，慢指针就是倒数第K个节点。

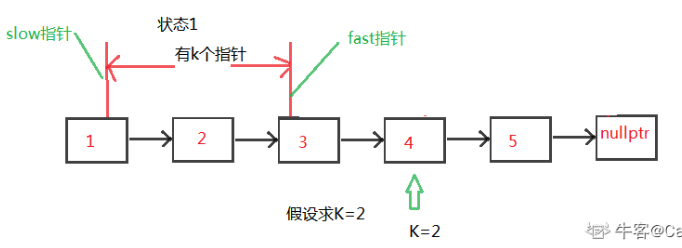
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
        ListNode* slowNode = pListHead;
        while (k != 0) {
            k--;
            if (pListHead != nullptr)
                pListHead = pListHead->next;
            else
                return nullptr;
        }
        while (pListHead != nullptr) {
            slowNode = slowNode->next;
            pListHead = pListHead->next;
        }
        return slowNode;
    }

 

NO15 、反转链表

【图文解析】反转一个单链表_反转链表_giturtle的博客-CSDN博客

以下开始逆序链表逻辑：在当前指针不为NULL时，先对原链表做头删操作，再对新链表做头插操作。即使用循环进行操作：

1.让node指针指向传入函数链表的头指针head，两指针指向保持相同。

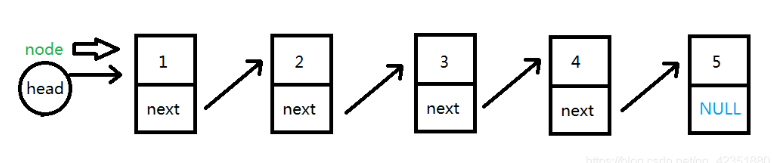
 2.然后让head指针指向它的next结点，此时旧链表已经完成了头删操作。第一个结点已经被"切割"下来。接下来要做的就是对新链表进行头插操作，使结点放入新链表。

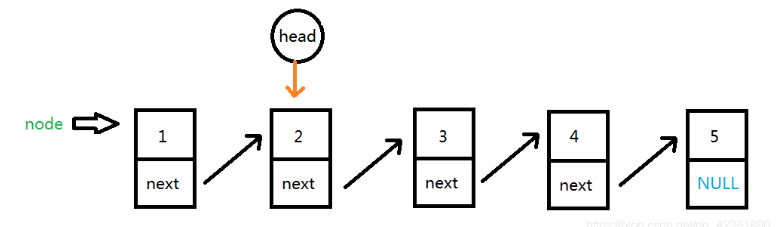
3.让node指针的next下一个结点指向新链表的头指针newHead，完成结点的链接，即头插入新的链表中。然后更新newHead指向为新链表的头结点。进行下一次循环。

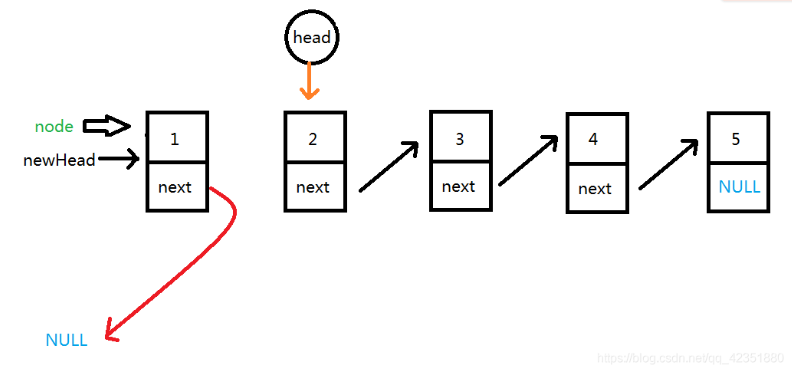
4. 最终head指针指向了原链表的结尾，即为NULL，退出循环，此时新链表已经反转完毕，情况如图：

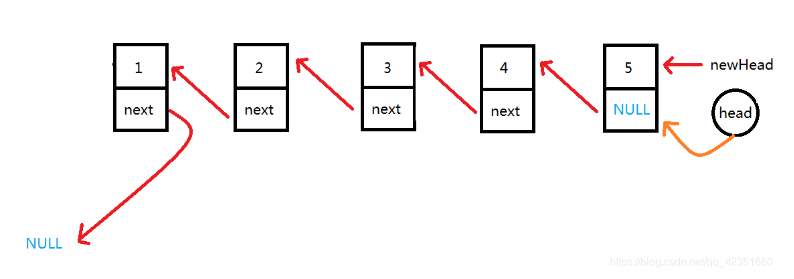
ListNode* ReverseList(ListNode* head) {
        // write code here
        struct ListNode* newHead = NULL;
        struct ListNode* node = (ListNode*)malloc(sizeof(struct ListNode));
        while (head != NULL) {
            //1. 对之前的链表做头删
            node = head;
            head = head->next;
            //2. 对新链表做头插
            node->next = newHead;
            newHead = node;
        }
        return newHead;
    }

 

NO16、合并两个有序链表

• step 1：判断空链表的情况，只要有一个链表为空，那答案必定就是另一个链表了，就算另一个链表也为空。
• step 2：新建一个空的表头后面连接两个链表排序后的节点，两个指针分别指向两链表头。
• step 3：遍历两个链表都不为空的情况，取较小值添加在新的链表后面，每次只把被添加的链表的指针后移。
• step 4：遍历到最后肯定有一个链表还有剩余的节点，它们的值将大于前面所有的，直接连在新的链表后面即可。

ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        // write code here
        if(pHead1 == NULL) return pHead2;
        if(pHead2 == NULL) return pHead1;
        ListNode* head = new ListNode(0);
        ListNode *cur = head;
        while(pHead1 && pHead2){
            if(pHead1->val <= pHead2->val){
                cur->next= pHead1;
                pHead1=pHead1->next;
            }
            else {
                cur->next=pHead2;
                pHead2= pHead2->next;
            }
            cur=cur->next;  
        }
        if(pHead1)
                cur->next = pHead2;
            else
                cur->next=pHead1;
        return head->next;

    }

 

 

1.队列

No22、从上往下打印二叉树

 

判断一个数是否为奇数

if(v&1)    //奇数

if(!(v&1))    //奇数

 

 copy函数

#include <algorithm>
copy(buf.begin(), buf.end(), nums.begin());

表示将buf中的元素赋值给nums。特别要注意它们之间的维数！

 

No1、二维数组中的查找

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

[

[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]

]

给定 target = 7，返回 true。

给定 target = 3，返回 false。

 

数据范围：矩阵的长宽满足 0≤n,m≤5000≤n,m≤500 ， 矩阵中的值满足 0≤val≤1090≤val≤10^9
进阶：空间复杂度 O(1) ，时间复杂度 O(n+m)

输入：7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]

返回值：true

说明：存在7，返回true   

---

题解一：暴力搜索

解题思路： 逐行逐列的搜索二维数组，判断是否存在目标值。

class Solution
{
public:
    bool Find(int target, vector<vector<int> > array)
    {
        for (auto i : array) {
            for (auto j : i)
            {
                if (j == target)
                    return true;
            }
        }
        return false;
    }
};

题解三： 线性搜索

解题思路：利用二维数组行列递增特性
主要思路：

1. 由于行列递增，可以得出：
   a.在一列中的某个数字，其上的数字都比它小
   b.在一行中的某个数字，其右的数字都比它大
2. 搜索流程：
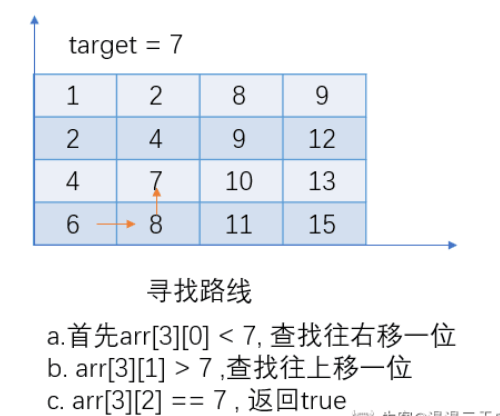
   a.首先从数组左下角搜索.
   b.如果当前数字大于target,那么查找往上移一位,如果当前数字小于target,那么查找往右移一位。
   c.查找到target,返回true; 如果越界，返回false;   

示例如下：

class Solution2
{
    bool Find(int target, vector<vector<int >>array)
    {
        if (array.size() == 0) return false;
        int r = array.size();
        int l = array[0].size();
        int left = 0, down = r - 1;
        while (left < 1 && down >= 0)
        {
            int tmp = array[down][left];
            if (tmp == target) return true;
            else if (tmp < target)
                left++;
            else down--;
        }
        return false;
    }
};

 

NO11.二进制中1的个数

 

算法思路二：巧用 n&(n-1)

n&(n - 1)，其预算结果恰为把 n 的二进制位中的最低位的 1 变为 0之后的结果

算法流程：

初始化数量统计变量 res
循环消去最右边的 1 ：当 n = 0时跳出。
res += 1 ： 统计变量加 1 ；
n &= n - 1 ： 消去数字 n 最右边的 1 。
返回统计数量 res。

int NumberOf1(int n) {
        // write code here
        int count = 0;
        while(n!=0){
            n=n&(n-1);
            count++;
        }
        return count;
    }

 

 

 

 No 65 矩阵中的路径