[SNOI2024] 拉丁方 题解

[SNOI2024] 拉丁方 题解

UPD：改了一下 \(n=R\) 一定有解的证明，之前那个有点模糊。

---

先看 CF600F。（题解先鸽了）

---

写一下吧，晚上说的东西有点混乱，那个证明可以说是糊出来的，但除了那个结论其他没什么问题。其实举得例子是没错的，Qyun 举得那个例子是少一种颜色的边的，这样就没错了（当然，不唯一）：

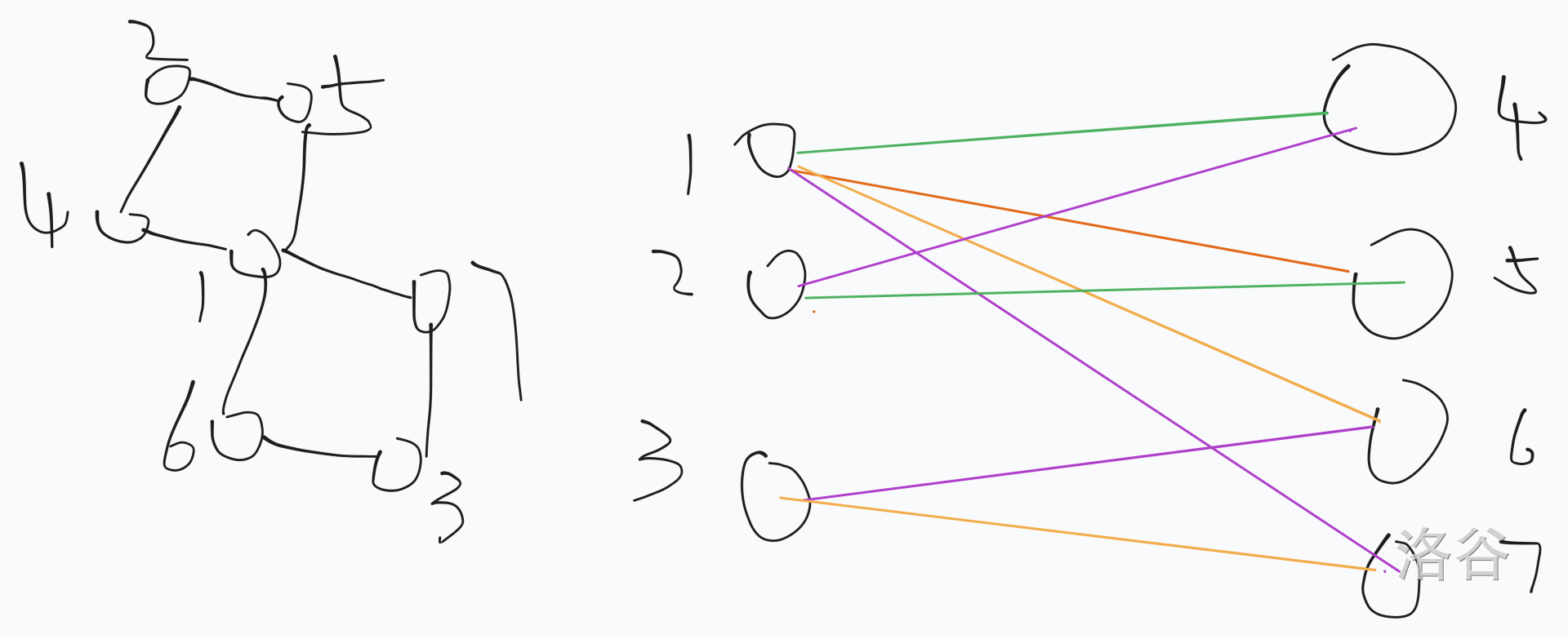
正文

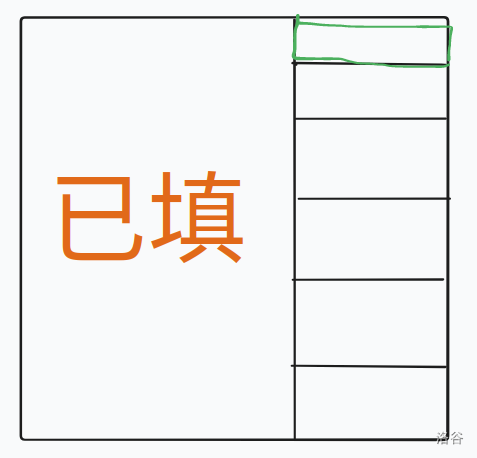
如果 \(n=R\) 就比较好做。（给了\(C=n\) 的部分分，一样）

把每个绿色部分抽象成一个二分图的左部点，右部点表示要填的数，向右部点连边表示绿色部分中可以填哪些数，每个点都向右连了 \(n-C\) 条边。现在要给这些边染色，颜色 \(i\) 表示第 \(C+i\) 列要填那个右部点。明显，相邻的边不能是同颜色的：对于左部，每一行不能有一样的数；对于右部，每一列不能有一样的数。

根据 Hall 定理，这个二分图最大匹配数为 \(n\)，也就是左边的都能匹配上（把所有边的颜色看为 \(1\)），也就是第 \(R+1\) 列一定能有一种合法方案，把 \(R+1\) 列填上，然后就是一模一样的子问题了。

根据 CF600F 的构造方法构造。正好是 \(n-C\) 种颜色（至于为什么“正好”，因为一定合法），所以就直接做完了。

---

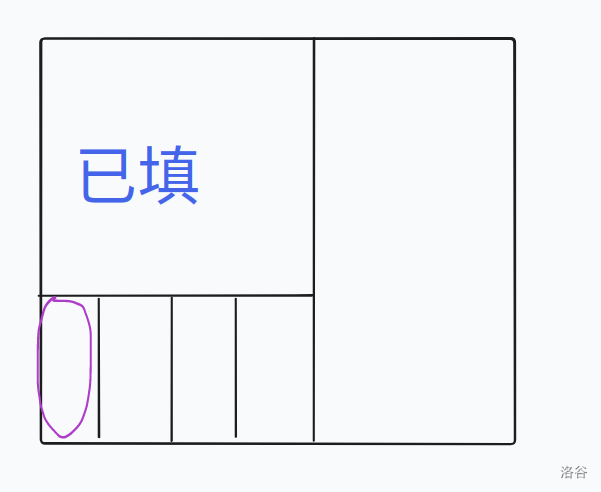
至于 \(n\ne R\)：

这里需要说下无解情况。

这个二分图要染色的最小颜色数（也就是最大度数）如果大于 \(n-R\) ，则无解，因为我们每列只能填 \(n-R\) 个数，也就是我们只有 \(n-R\) 中颜色可以填，多了当然无解。

然后和上面一样构造，我们只要合法就行，不用考虑那么多，因为如果已经合法那右边一定有合法方案。

#include <bits/stdc++.h>

using namespace std;

#define IL inline
#define vec vector
#define fi first
#define se second
using pii = pair<int, int>;

IL int _R() { int x; cin >> x; return x; }
IL void ckx(int &x, const int &y) { (x < y) && (x = y); }

const int N = 500;
const int maxN = N + 3;

int n, R, C;
int a[maxN][maxN];

int to[maxN + N][maxN];
namespace Paint {
  void init() { memset(to, 0, sizeof(to)); }
  void add(int u, int v) {
    int c1 = 1, c2 = 1;
    while (to[u][c1]) c1++;
    while (to[v][c2]) c2++;
    to[u][c1] = v, to[v][c2] = u;
    if (c1 != c2)
      for (int c = c2, x = v; x; x = to[x][c], c ^= c1 ^ c2)
        swap(to[x][c1], to[x][c2]); 
  }
}

int cnt[maxN];
bool mp[maxN];
bool wk1() {
  for (int i = 1; i <= n; i++) cnt[i] = C;
  for (int i = 1; i <= R; i++)
    for (int j = 1; j <= C; j++)
      cnt[a[i][j]]--;
  for (int i = 1; i <= n; i++)
    if (cnt[i] > n - R) return false;

  Paint::init();
  for (int j = 1; j <= C; j++) {
    memset(mp, false, sizeof(mp));
    for (int i = 1; i <= R; i++) mp[a[i][j]] = true;
    for (int i = 1; i <= n; i++)
      if (!mp[i]) Paint::add(j, n + i);
  }
  for (int j = 1; j <= C; j++)
    for (int i = R + 1; i <= n; i++)
      a[i][j] = to[j][i - R] - n;
  return true;
}
void wk2() {
  Paint::init();
  for (int i = 1; i <= n; i++) {
    memset(mp, false, sizeof(mp));
    for (int j = 1; j <= C; j++) mp[a[i][j]] = true;
    for (int j = 1; j <= n; j++)
      if (!mp[j]) Paint::add(i, n + j);
  }
  for (int i = 1; i <= n; i++)
    for (int j = C + 1; j <= n; j++)
      a[i][j] = to[i][j - C] - n;
}

void Main() {
  n = _R(), R = _R(), C = _R();
  for (int i = 1; i <= R; i++)
    for (int j = 1; j <= C; j++)
      a[i][j] = _R();

  if (R != n)
    if (!wk1())
      return cout << "No\n", void();
  wk2();

  cout << "Yes\n";
  for (int i = 1; i <= n; i++, cout << '\n')
    for (int j = 1; j <= n; j++)
      cout << a[i][j] << ' ';
}

int main() {
  freopen("latin.in", "r", stdin);
  freopen("latin.out", "w", stdout);

  cin.tie(nullptr)->sync_with_stdio(false);

  int Tims = _R();
  while (Tims--) Main();
}