P11503 [NordicOI 2018] Nordic Camping
P11503 [NordicOI 2018] Nordic Camping
花了我挺长时间。
帐篷都是正方形的,可以枚举左上角,二分正方形边长,二维前缀和判断是否合法。这部分复杂度为 \(O(n^2\log n)\)。处理出来后,问题似乎就变成了矩形取最大值,单点查询。直接做是 \(\log^2\) 的,65 pts。具体就是,先扫描线(扫描线竖向),我们类似标记永久化,但修改的标记我们记录到线段树中每个节点中(可以随便用 STL 维护,例如 set、优先队列懒惰删除),撤销的时候暴力删除。
然后就考虑需要发现一点性质,我们所谓的“矩形取最大值,单点查询”,矩形全是正方形,值是正方形的面积。
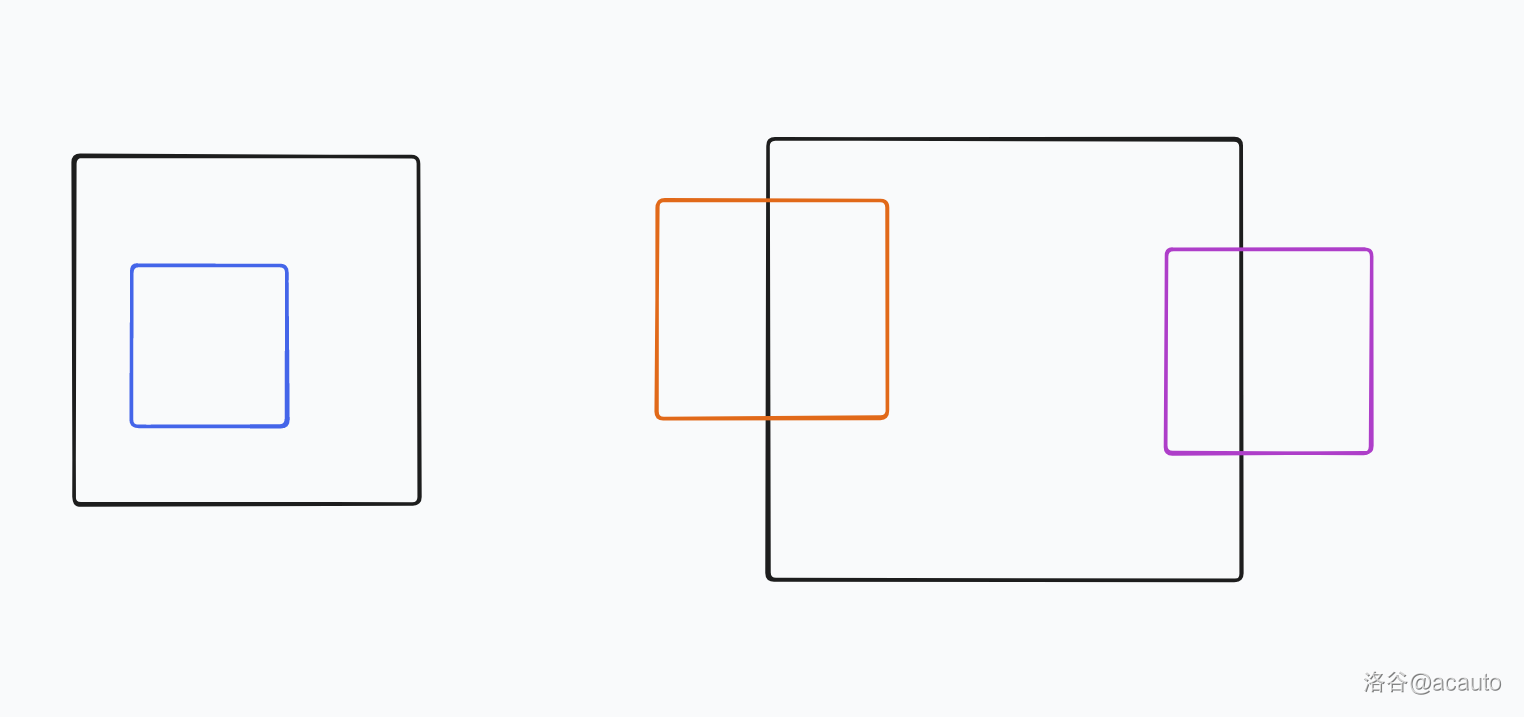
我们依旧扫描线。考虑上面几种情况,蓝色正方形没有任何影响不用考虑。橙色正方形和黑色正方形重叠的部分,答案肯定是黑色,这时候橙色正方形对后面就没有任何影响了。粉色正方形影响的范围比黑色远,它还是可能有用的。这其实就是单调队列的过程,把上面的 STL 替换为单调队列,复杂度被优化为 \(O(n^2\log n)\)。
#include <bits/stdc++.h>
using namespace std;
#define IL inline
#define fi first
#define se second
using pii = pair<int, int>;
using ubt = long long;
IL void ckx(int &x, const int &y) { (x < y) && (x = y); }
const int N = 2000, M = 1e5;
const int maxN = N + 3, maxM = M + 3;
#define ls (p << 1)
#define rs (p << 1 | 1)
int NOW;
deque<pii> t[maxN << 2];
void C(int L, int R, int T, int v, int p, int l, int r) {
if (L <= l && r <= R) {
if (!t[p].empty() && t[p].back().se >= T) return; // 蓝色无用
while (!t[p].empty() && t[p].back().fi <= v) t[p].pop_back();
t[p].emplace_back(v, T);
return;
}
int mid = (l + r) >> 1;
if (L <= mid) C(L, R, T, v, ls, l, mid);
if (R > mid) C(L, R, T, v, rs, mid + 1, r);
}
void ask(int K, int p, int l, int r, int &ans) {
while (!t[p].empty() && t[p].front().se < NOW) t[p].pop_front();
if (!t[p].empty()) ckx(ans, t[p].front().fi);
if (l == r) return;
int mid = (l + r) >> 1;
if (K <= mid) ask(K, ls, l, mid, ans);
else ask(K, rs, mid + 1, r, ans);
}
int n, m;
char c[maxN][maxN];
int s[maxN][maxN];
IL int get(int x, int y, int a, int b) {
return s[a][b] - s[a][y - 1] - s[x - 1][b] + s[x - 1][y - 1];
}
int tot;
struct Modi {
int y, l, r, v, T;
} mo[N * N + 3];
int Q;
struct ques {
int x, y, id;
} q[maxM];
int ans[maxM];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
do c[i][j] = getchar(); while (c[i][j] != '.' && c[i][j] != '#');
s[i][j] = c[i][j] == '#';
}
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
for (int x = 1; x <= n; ++x)
for (int y = 1; y <= m; ++y) if (c[x][y] != '#') {
int l = 1, r = min(n - x + 1, m - y + 1);
while (l <= r) {
int mid = (l + r) >> 1;
if (!get(x, y, x + mid - 1, y + mid - 1))
l = mid + 1;
else r = mid - 1;
}
mo[++tot] = {y, x, x + r - 1, r, y + r - 1};
}
sort(mo + 1, mo + tot + 1, [](const auto &A, const auto &B) {
return A.y < B.y;
});
scanf("%d", &Q);
for (int i = 1; i <= Q; ++i)
scanf("%d %d", &q[i].x, &q[i].y), q[i].id = i;
sort(q + 1, q + Q + 1, [](const auto &A, const auto &B) {
return A.y < B.y;
});
int now = 1;
for (int i = 1; i <= Q; ++i) {
NOW = q[i].y;
while (now <= tot && mo[now].y <= q[i].y) {
C(mo[now].l, mo[now].r, mo[now].T, mo[now].v, 1, 1, n);
now++;
}
ask(q[i].x, 1, 1, n, ans[q[i].id]);
}
for (int i = 1; i <= Q; ++i)
printf("%d\n", ans[i] * ans[i]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号