Java数据结构与算法(三)--栈
目录
在第一章我们讲了数据这个具体的数据储存结构,它主要应用与数据的记录。
本章主要讲一个构思算法的辅助工具--栈,用它来执行特定的任务。
1.栈的基本概念
栈(stack)是一种抽象的数据结构(ADT),它可以用其他的数据结构来实现,比如说前面讲过的数组。
它是一种受限访问的数据结构,遵循先进后出(FILO)的规则,即最先进入栈的最后出来的原则。
它就像子弹夹一样,先压入弹夹的子弹,压到最下面,最后射出去。
根据栈的特性,在树的搜索与深度优先搜索(DFS)中,栈可以发挥重要的作用
2.栈的简单实现
public class MyStack { //储存 private int[] array; //栈的顶部 private int top; //最大容量 private int max; public MyStack(int size){ max = size; top = -1; array = new int[size]; } //压入数据 public void push(int x){ if((top+1)<max){ array[++top]=x; } } //弹出数据 public int pop(){ return array[top--]; } //获取栈顶数据 public int peek(){ return array[top]; } //栈是否为空 public boolean isEmpty(){ return top==-1; } //栈是否满了 public boolean isFull(){ return top == max-1; } public static void main(String[] args) { MyStack stack = new MyStack(10); stack.push(3); stack.push(2); stack.push(1); System.out.println(stack.peek()); while (!stack.isEmpty()){ System.out.println(stack.pop()); } } }
看下测试结果:
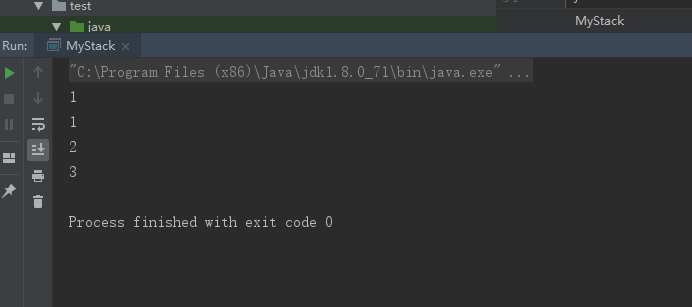
上面我们用数组实现了一个简单的栈,用top指向栈顶元素,压入和弹出只需要移动栈顶指针并判断是否超过最大容量即可。
不过这个栈有个问题就是,容量有限制,我们必须初始化一个恰当大小的容量,才能完全放置数据并不会浪费容量。
这比较难做到,我们来参考java中stack的实现来优化以下这个栈
3.代码解析
我们可以参考public class Stack<E> extends Vector<E> 这个实现类。实际JDK推荐使用Deque的实现类来实现栈。
这个Stack仅做参考:
protected Object[] elementData;//使用Object储存数据
//添加了扩容机制 //创建一个大小为当前容量的2倍的数组 //将旧的数据移动到新的数组中 private void grow(int minCapacity) { // overflow-conscious code int oldCapacity = elementData.length; int newCapacity = oldCapacity + ((capacityIncrement > 0) ? capacityIncrement : oldCapacity); if (newCapacity - minCapacity < 0) newCapacity = minCapacity; if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity); elementData = Arrays.copyOf(elementData, newCapacity); }
在来看下ArrayQueue如何实现栈的:
//ArrayDeque poll的实现方法 public E pollFirst() { int h = head; @SuppressWarnings("unchecked") E result = (E) elements[h]; // Element is null if deque empty if (result == null) return null; elements[h] = null; // Must null out slot head = (h + 1) & (elements.length - 1); return result; }
head = (h + 1) & (elements.length - 1);
一个巧妙的设计,一般情况就是head+1,在head达到数组末端的时候,将head置0。
4.应用场景
利用栈的特性我们可以用栈达到逆转字符的作用
//把前面存储的int[]改成Object[] public static void main(String[] args) { MyStack stack = new MyStack(20); String str = "Hello World!"; char[] chars = str.toCharArray(); for(char c: chars){ stack.push(c); } while (!stack.isEmpty()){ System.out.print(stack.pop()); } }
运行结果:
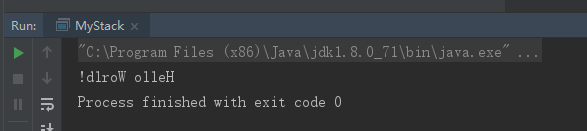
有了前面这个小例子,我们在举个实现应用的例子。我们可能需要解析一串字符表示的表达式,
通常做法,可以将字串转变为逆波兰表达式(后缀表达式)去计算
比如将 (a+b)*(c+d) 转变为 ab+cd+*
只需两两进行简单计算即可
/** * 转变为逆波兰表达式 * @param strList * @return */ public List<String> initRPN(List<String> strList){ List<String> returnList = new ArrayList<String>(); //用来存放操作符的栈,这里的栈是前面自定义的栈也可以用ArrayQueue Stack stack = new Stack(); int length = strList.size(); for(int i=0;i<length;i++ ){ String str = strList.get(i); if(isNumber(str)){//如果是数字直接放入表达式,等待操作 returnList.add(str); }else{//操作字符进行优先级判断 if(str.equals(OPSTART)){ //'('直接入栈 stack.push(str); }else if(str.equals(OPEND)){ //')' //进行出栈操作,直到栈为空或者遇到第一个左括号 while (!stack.isEmpty()) { //将栈顶字符串做出栈操作 String tempC = stack.pop(); if (!tempC.equals(OPSTART)) { //如果不是左括号,则将字符串直接放到逆波兰链表的最后 returnList.add(tempC); }else{ //如果是左括号,退出循环操作 break; } } }else{ if (stack.isEmpty()) { //如果栈内为空 //将当前字符串直接压栈 stack.push(str); }else{ //栈不空,比较运算符优先级顺序 if(precedence(stack.top())>=precedence(str)){ //如果栈顶元素优先级大于当前元素优先级则 while(!stack.isEmpty() && precedence(stack.top())>=precedence(str)){ returnList.add(stack.pop()); } } stack.push(str); } } } } //如果栈不为空,则将栈中所有元素出栈放到逆波兰链表的最后 while (!stack.isEmpty()) { returnList.add(stack.pop()); } return returnList; }
/**
* 设置优先级顺序()设置与否无所谓
* @return
*/
private int precedence(String str){
char sign = str.charAt(0);
switch(sign){
case '+':
case '-':
return 1;
case '*':
case '/':
return 2;
case '^':
case '%':
return 3;
case '(':
case ')':
// case '#':
default:
return 0;
}
}
/**
* 是否是整数或是浮点数,但默认-05.15这种也认为是正确的格式
* @param str
* @return
*/
private boolean isNumber(String str){
Pattern p = Pattern.compile("^(-?\\d+)(\\.\\d+)?$");
Matcher m = p.matcher(str);
boolean isNumber = m.matches();
return isNumber;
}
以上罗列了部分代码,主要代码就是遇到普通字符入栈,遇到操作字符,比较操作字符优先级在进行出栈操作。
5.总结
根据栈先进后出的特性,我们可以实现多种功能。
栈通过提供限制性的访问方法push()和pop(),使得程序不容易出错。
栈只对栈顶元素进行操作,出栈和入栈的时间复杂度都为O(1)
栈的操作与栈中数据个数无关,因此也不需要比较和移动操作。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号