指数型递归

、

从 1∼n1∼n 这 nn 个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 nn。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 11 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1≤n≤151≤n≤15

输入样例：

3

输出样例：

3
2
2 3
1
1 3
1 2
1 2 3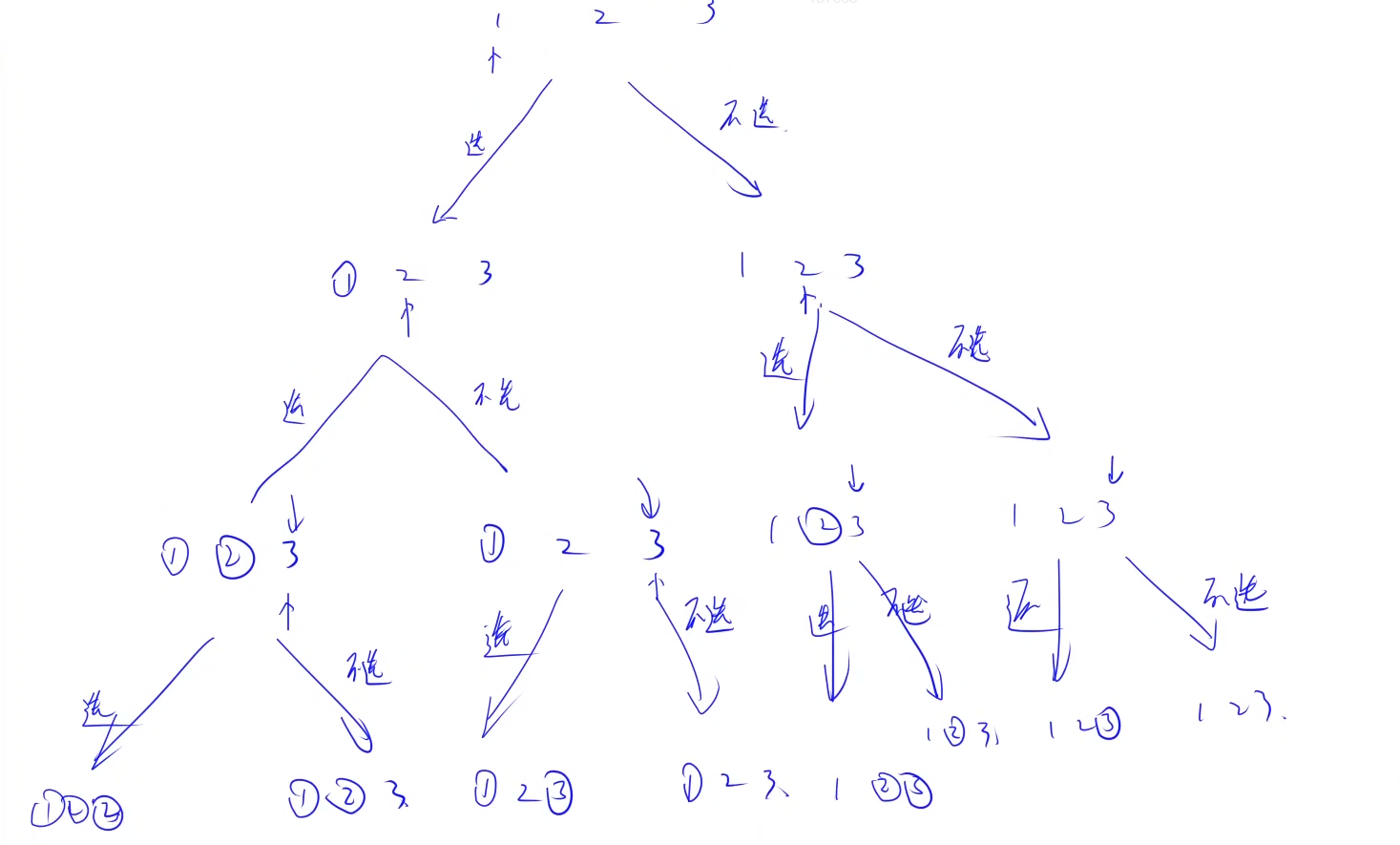

 

 这个就是地柜二叉搜索树。在每次搜索之前要想好dfs的参数是啥

之前一般都是dfs(int u)//u为深度

而这里的深度就是每一层往下选第几个数

还需要定一个参数，在每一层也就是每次选择的第几个数选还是不选这两种方案

所以大概思路就能出来了

#include<iostream>
using namespace std;
int n;
const int N=20;
bool st[N];
void dfs(int u)//深度，就是每一层为选择的第几个数字 
{
    if(u>n)
    {
        for(int i=1;i<=n;i++)
            if(st[i])
                 cout<<i<<" ";
        cout<<endl;
        return ;
    }
    st[u]=true;
    dfs(u+1);
    st[u]=false;
    dfs(u+1);
}
int main(){
    cin>>n;
    dfs(1);
    return 0;
}

看图说话