百度Intern面试题之二叉树的网络传输及恢复–二叉树的文件存储和读取

  这不是我的面试题，是一个同学在百度的面试题。

  要求将一颗二叉树通过网络传输到给另一个客户端，并且在该客户端恢复为原始二叉树。

 

  这道题目可以理解为如何将一颗二叉树存储到文件中，并且读取后正确恢复。

 

  以这样的一棵二叉树为例：

 

 

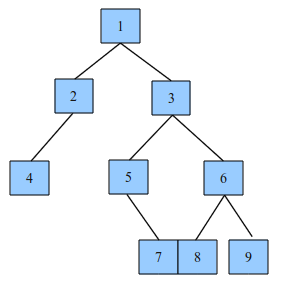
  我想到了三种解决方法：

  1. 二叉树补全法，将这课二叉树补全，变成一颗完全二叉树，再使用数组进行存储，写入文件中。这样做需要在节点中增加一个属性，标记是否为补全的节点。

  这种方法不太合理，因为使用了补全操作，对于一颗很不规则的二叉树，将会占用非常大的存储空间，并且修改了二叉树的属性。

  2. 游标实现法。定义一个新的结构体，其中的left和right指针修改为结构体在数组中的位置。

  就像下面这样，数组的第一个位置表示NULL位置，剩余的存放节点，left和right分别指向左右子节点所在数组索引。这是前序遍历递归调用得到的数组。

 

  3. 二叉树位置描述实现。同2类似，不过这里没有左右子节点的指针，而是用一个整形来描述当前节点在一颗完全二叉树中的位置。显然，在上图这样的二叉树中，节点1的位置为1,节点2的位置为2，节点3的位置为3，节点4的位置为4，节点5的位置为6，依次类推。。。

 

  依次，可以定义一个新的结构体描述节点信息，用于存储。

typedef struct BTreeNodeFile 
{
	Element e; //节点值
	Position p; //节点在完全二叉树中的位置
} BTreeNodeFile;

 

  于是可以前序遍历递归调用，得到这样的一个数组。

 

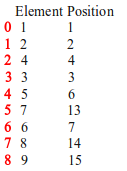
  恢复的时候，查找左右子节点，只需要查找p值2倍于自身以及2倍+1于自身的节点。

 

  下面就是对与方法3的C++源码。

 

#ifndef TREE_H_
#define TREE_H_
typedef int Element;
typedef struct BTreeNode
{
	Element e;
	BTreeNode *left;
	BTreeNode *right;
}BTreeNode;

typedef struct BTree
{
	BTreeNode *root;
	unsigned int count;
}BTree;

typedef BTreeNode* BTreeNodePtr;
typedef BTree* BTreePtr;
#endif

 

 

#include <iostream>
#include <map>
#include <stdio.h>
#include <string.h>
#include "tree.h"
using namespace std;
typedef int Position;
typedef struct BTreeNodeFile
 {
	Element e; //节点值
	Position p; //节点在完全二叉树中的位置
} BTreeNodeFile;

typedef map<int, BTreeNodePtr> NodeMap;
const char fileName[] = "btree.dat";
FILE *filePtr;
void writeNode(const BTreeNodePtr btn, Position p)
 {
	if (!btn) return;

	BTreeNodeFile node;
	node.e = btn->e;
	node.p = p;
	//写入当前节点
	fwrite(&node, sizeof(node), 1, filePtr);
	//写入左子树
	writeNode(btn->left, 2 * p);
	//写入右子树
	writeNode(btn->right, 2 * p + 1);
}

void writeBTree(const BTreePtr bt)
{
	filePtr = fopen(fileName, "w");
	fwrite(&bt->count, sizeof(bt->count), (size_t) 1, filePtr); //写入节点个数
	writeNode(bt->root, 1); //写入节点
	fclose(filePtr);
}

BTreePtr readBTree()
 {
	BTreePtr bt = new BTree;
	NodeMap mapNode;
	BTreeNodeFile btnf;
	BTreeNode *btn;
	filePtr = fopen(fileName, "r");
	fread(&(bt->count), sizeof(bt->count), 1, filePtr); //读入结点个数

	while (fread(&btnf, sizeof(btnf), (size_t) 1, filePtr) > 0) 
        {
		btn = new BTreeNode;
		btn->e = btnf.e;
		mapNode.insert(NodeMap::value_type(btnf.p, btn));
	}

	NodeMap::iterator iter;
	NodeMap::iterator iter_t;

	for (iter = mapNode.begin(); iter != mapNode.end(); iter++)
        {
		iter_t = mapNode.find(2 * iter->first);

		if (iter_t != mapNode.end())
                { //找到左儿子
			iter->second->left = iter_t->second;
		} 
                else 
                {	//未找到左儿子
			iter->second->left = NULL;
		}

		iter_t = mapNode.find(2 * iter->first + 1);

		if (iter_t != mapNode.end()) { //找到右儿子
			iter->second->right = iter_t->second;
		} 
                else 
                {	//未找到右儿子
			iter->second->right = NULL;<br />
		}
	}

	iter_t = mapNode.find(1); //找root节点
	if (iter_t != mapNode.end()) {
		bt->root = iter_t->second;
	}
	fclose(filePtr);
	return bt;
}

BTreePtr buildBTree() 
{
	BTreePtr bt = new BTree;
	BTreeNodePtr btn = new BTreeNode[9];
	for (int i = 0; i < 9; i++)
        {
		memset(&btn[i], 0, sizeof(BTreeNode));
		btn[i].e = i;
	}
	btn[0].left = &btn[1];
	btn[1].left = &btn[3];
	btn[2].left = &btn[4];
	btn[5].left = &btn[7];
	btn[0].right = &btn[2];
	btn[2].right = &btn[5];
	btn[4].right = &btn[6];
	btn[5].right = &btn[8];
	bt->root = &btn[0];
	bt->count = 9;
	return bt;
}

void printSubBTree(BTreeNodePtr btn, int lvl) 
{
	int i;
	if (!btn)
		return;
	for (i = 0; i < lvl; i++)
		printf("  ");
	printf("%d/n", btn->e + 1);
	printSubBTree(btn->left, lvl + 1);
	printSubBTree(btn->right, lvl + 1);
}

void printBTree(BTreePtr bt)
{
	printSubBTree(bt->root, 0);
}

int main() 
{
	BTreePtr bt = buildBTree();
	printBTree(bt);
	writeBTree(bt);
	bt = readBTree();
	printBTree(bt);
	return 0;
}
                                

 

 

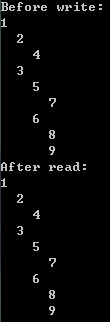
  这是该程序的输出结果：