图论学习笔记
图
图是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系!
点一般用字母v表示,如v1,v2,v3,v4。
一些简单的术语
基本定义:
- 图:一张图 \(G\) 由若干个点和连接这些点的边构成。称点的集合为点集 \(V\),边的集合为边集 \(E\),记 \(G=(V,E)\)。
- 阶:图 \(G\) 的点数 \(|V|\) 称为阶,记作 \(|G|\)。
- 无向图:若 \(e\in E\) 没有方向,则称 \(G\) 为无向图。无向图的边记作 \(e = (u, v)\),\(u, v\) 之间无序。
- 有向图:若 \(e\in E\) 有方向,则称 \(G\) 为有向图。有向图的边记作 \(e = u\to v\) 或 \(e = (u, v)\),\(u, v\) 之间有序。无向边 \((u, v)\) 可以视为两条有向边 \(u\to v\) 和 \(v\to u\)。
- 重边:端点和方向(有向图)完全相同的边称为重边。
- 自环:连接相同点的边称为自环。
相邻相关:
- 相邻:在无向图中,称 \(u,v\) 相邻当且仅当存在 \(e=(u, v)\)。
- 邻域:在无向图中,点 \(u\) 的邻域为所有与之相邻的点的集合,记作 \(N(u)\)。
- 邻边:在无向图中,与 \(u\) 相连的边 \((u,v)\) 称为 \(u\) 的邻边。
- 出边 / 入边:在有向图中,从 \(u\) 出发的边 \(u\to v\) 称为 \(u\) 的出边,到达 \(u\) 的边 \(v\to u\) 称为 \(u\) 的入边。
- 度数:一个点的度数为与之关联的边的数量,记作 \(d(u)\),\(d(u)=\sum_{e\in E}([u=e_u]+[u=e_v])\)。每个点的自环对其度数产生 \(2\) 的贡献。
- 出度/入度:在有向图中,从 \(u\) 出发的边的数量称为 \(u\) 的出度,记作 \(d ^ +(u)\);到达 \(u\) 的边的数量称为 \(u\) 的入度,记作 \(d ^ -(u)\)。
路径相关:
- 途径:连接一串结点的序列称为途径,用点序列 \(v_{0..k}\) 和边序列 \(e_{1..k}\) 描述,其中 \(e_i=(v_{i-1},v_i)\)。通常写为 \(v_0\to v_1\to \cdots\to v_k\)。
- 迹:不经过重复边的途径称为迹。
- 回路:\(v_0=v_k\) 的迹称为回路。
- 路径:不经过重复点的迹称为路径,也称简单路径。不经过重复点比不经过重复边强,所以不经过重复点的途径也是路径。注意题目中的简单路径可能指迹。
- 环:除 \(v_0=v_k\) 外所有点互不相同的途径称为环,也称圈或简单环。
- 路径:一些边组成的序列,满足第一条边的终点为第二条边的起点,第二条边的终点为第三条边的起点...如果边有权值,则我们把这些边权的和作为路径的长度;如果没有权值,则我们把边的条数作为路径的长度,即可以看作每条边的权值为1
- 点/边的权值:点/边的属性,题目可能会用到。
- 重边:起点与终点都相同的边被称为重边
- 自环:点到自己有一条边
- 简单路径:如果路径中没有经过重复点,则我们称这条路径为简单路径
- 环:起点和终点相同的简单路径
- 子图:在原图的边和点中选择一些保留下来,其他删除,就是子图
- 连通性相关:两个点之间有路径,则称两点之间互相联通
特殊图:
- 简单图:不含重边和自环的图称为简单图。
- 有向无环图:不含环的有向图称为有向无环图,简称DAG(directed Acyclic Graph)。
- 完全图:任意不同的两点之间恰有一条边的无向简单图称为完全图。\(n\) 阶完全图记作 \(K_n\)。
- 树:不含环的无向连通图称为树。树是简单图,满足 \(|V|=|E|+1\)。若干棵(包括一棵)树组成的连通块称为森林。
- 稀疏图/稠密图:\(|E|\) 远小于 \(|V|^2\) 的图称为稀疏图,\(|E|\) 接近 \(|V|^2\) 的图称为稠密图。这两个概念没有严格定义,用于讨论时间复杂度为 \(\mathcal{O}(|E|)\) 和 \(\mathcal{O}(|V|^2)\) 的算法。
子图相关:
- 子图:满足 \(V'\subseteq V\) 且 \(E'\subseteq E\) 的图 \(G'=(V',E')\) 称为 \(G=(V,E)\) 的子图,记作 \(G'\subseteq G\)。
- 导出子图:选择若干个点以及两端都在该点集的所有边构成的子图称为该图的导出子图。导出子图的形态仅由选择的点集 \(V'\) 决定,称点集为 \(V'\) 的导出子图为 \(V'\) 导出的子图,记作 \(G[V']\)。
- 生成子图:\(|V'| = |V|\) 的子图称为生成子图。
- 极大子图(分量):在子图满足某性质的前提下,称子图 \(G'\) 是 极大 的,当且仅当不存在同样满足该性质的子图 \(G''\) 且 \(G'\subsetneq G''\subseteq G\)。称 \(G'\) 为满足该性质的分量,如连通分量,点双连通分量。极大子图不能再扩张。例如,极大的连通的子图称为原图的连通分量,也就是我们熟知的连通块。
存图
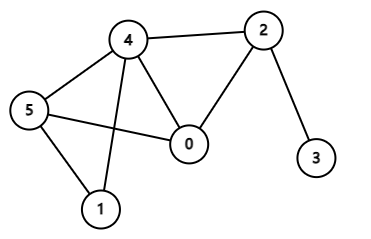
有以下边:
0 2
0 4
0 5
1 4
1 5
2 3
2 4
4 5
1.邻接矩阵
存储方式如下表:
| \ | v0 | v1 | v2 | v3 | v4 | v5 |
|---|---|---|---|---|---|---|
| v0 | - | - | 1 | - | 1 | 1 |
| v1 | - | - | - | - | 1 | 1 |
| v2 | 1 | - | - | 1 | 1 | - |
| v3 | - | - | 1 | - | - | - |
| v4 | 1 | 1 | 1 | - | - | 1 |
| v5 | 1 | 1 | - | - | 1 | - |
每一条边(记为\((x,y)\))都将\(a[x][y]\)存为\((x,y)\)的长度(无向图也要把边\((y,x)\)存入)
但可以看到有很多-,也就是浪费了很多空间(开了\(n^2\)的空间却只用了m,一般\(m\le 2*n\))
所以可以优化
2.邻接表
0 2
0 4
0 5
1 4
1 5
2 3
2 4
4 5
存储方式如下表:
| \ | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| v0 | 2 | 4 | 5 | - | - | - |
| v1 | 4 | 5 | - | - | - | - |
| v2 | 0 | 3 | 4 | - | - | - |
| v3 | 2 | - | - | - | - | - |
| v4 | 0 | 1 | 2 | 5 | - | - |
| v5 | 0 | 1 | 4 | - | - | - |
后面还是有很多空,但可以动态分配空间(vector或链表实现)
vector实现
struct node{
int to,len;
}//结构体
/////////////////////////////加边/////////////////////////////
void add(int x,int y,int s){
v[x].push_back(node{y,i});
//v[y].push_back(node{x,i});当为无向图时要反向加边
}
/////////////////////////////遍历/////////////////////////////
//单点
for(int i=0;i<v[x].size();i++)/*边为v[x][i]*/;
//dfs序
void dfs(int a,int s){
if(b[a])return;
b[a]=1;
cout<<a<<" ";
for(int i=0;i<v[a].size();i++){
if(!b[v[a][i]])dfs(v[a][i],s+1);
}
}
//bfs序
void bfs(){
queue<int>q;
q.push(1);
while(!q.empty()){
int u=q.front();
q.pop();
if(b2[u])continue;
cout<<u<<" ";
b2[u]=1;
for(int i=0;i<v[u].size();i++)q.push(v[u][i]);
}
}
链表实现
int e[N],cnt,h[N];
struct node{
int to,len,next;
}//结构体
/////////////////////////////加边/////////////////////////////
void add(int x,int y,int s){
e[++cnt].to=y;
e[cnt].len=w;
e[cnt].next=h[x];
h[x]=cnt;
}
/////////////////////////////遍历/////////////////////////////
//单点
for(int i=h[x];i;i=e[i].next)/*用e[i]*/;
//dfs/bfs序遍历代码同
例题
点击查看P5318代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
vector<int>v[550000];
int n,m,l,r,T,b[550010]={0},b2[550010]={0};
void dfs(int a,int s){
if(b[a])return;
b[a]=1;
cout<<a<<" ";
for(int i=0;i<v[a].size();i++){
if(!b[v[a][i]]){
dfs(v[a][i],s+1);
}
}
}
void bfs(){
queue<int>q;
q.push(1);
while(!q.empty()){
int u=q.front();
q.pop();
if(b2[u])continue;
cout<<u<<" ";
b2[u]=1;
for(int i=0;i<v[u].size();i++){
q.push(v[u][i]);
}
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>l>>r;
v[l].push_back(r);
}
for(int i=1;i<=n;i++){
sort(v[i].begin(),v[i].end());
}
dfs(1,0);
cout<<endl;
bfs();
return 0;
}
B3643 图的存储
B3613 图的存储与出边的排序
P3916 图的遍历
全源最短路
Floyd
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
点击查看全代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,b[1005][1005];
int dp[1005][1005]={0};
signed main(){
cin>>n>>m;
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=n;i++){
dp[i][i]=0;
}
for(int i=0;i<m;i++){
int a,b,c;
cin>>a>>b>>c;
dp[a][b]=c;
dp[b][a]=c;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<dp[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
时间复杂度:\(O(N^3)\)
空间复杂度:\(O(N^2)\)
Johnson
分析
首先考虑求全源最短路的几种方法:
- floyd:时间复杂度\(O(n^3)\),可以处理负权边,但不能处理负环,而且速度很慢。
- Ford:以每个点为源点做一次Ford,时间复杂度\(O(n^2m)\),可以处理负权边,可以处理负环。
- dijkstra:以每个点为源点做一次dijkstra,时间复杂度\(O(nm\log m)\),不能处理负权边。
思想
建立一个超级源点\(s\),由它向其他的所有结点都连一条边权为\(0\)的边。
再将每条边加一个值,使它权值为正。
证明:
\(s -> p_1 -> p_2 -> \cdots -> p_k -> t\)
\(=(w_{s,p_1}+h_s-h_{p_1})+(w_{p_1,p_2}+h_{p_1}-h_{p_2})+\dots+(w_{p_k,t}+h_{p_k}-h_t)\)
\(=h_s+w_{s,p_1}+w_{p_1,p_2}+\cdots+w_{p_k,t}-h_t\)
根据三角形不等式(两边之和大于第三边)得:
任意一条边 \((u,v)\) 满足\(h_v \le w_{u,v}+h_u\),所以新边的边权为\(w_{u,v}+h_u-h_v\),它一定\(\ge 0\)
代码
点击查看代码
#include<bits/stdc++.h>
#define INF 1e9
using namespace std;
int n,m;
int b[100010],vis[100010];
long long cnt[100010],dis[100010],dis1[100010];
bool f[100010];
struct node{
int a,s;
};
vector<node>v[100010];
bool SPFA(int ff){
queue<int>q;
for(int i=0;i<=n;i++){
dis1[i]=INF;
cnt[i]=0;
b[i]=0;
}
q.push(ff);
b[ff]=1;
dis1[ff]=0;
cnt[ff]++;
while(!q.empty()){
int u=q.front();
q.pop();
b[u]=0;
for(int i=0;i<v[u].size();i++){
int a=v[u][i].a,s=v[u][i].s;
if(dis1[a]>dis1[u]+s){
dis1[a]=dis1[u]+s;
if(!b[a]){
b[a]=1;
q.push(a);
cnt[a]++;
if(cnt[a]>n){
return 1;
}
}
}
}
}
return 0;
}
struct dj{
int dis,bb;
bool operator < (const dj &a) const{
return a.dis<dis;
}
};
void dijkstra(int x){
priority_queue<dj>q;
for(int i=1;i<=n;i++)dis[i]=INF;
for(int i=1;i<=n;i++)vis[i]=0;
dis[x]=0;
q.push((dj){0,x});
while(!q.empty()){
dj now=q.top();
q.pop();
if(vis[now.bb])continue;
vis[now.bb]=1;
for(int i=0;i<v[now.bb].size();i++){
int to=v[now.bb][i].a,w=v[now.bb][i].s;
if(dis[to]>dis[now.bb]+w){
dis[to]=dis[now.bb]+w;
if(!vis[to])q.push((dj){dis[to],to});
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y,s;
cin>>x>>y>>s;
v[x].push_back(node{y,s});
}
for(int i=1;i<=n;i++)v[0].push_back(node{i,0});
if(SPFA(0)){
cout<<"-1";
return 0;
}
for(int u=1;u<=n;u++){
for(int i=0;i<v[u].size();i++){
v[u][i].s+=dis1[u]-dis1[v[u][i].a];//求新边的边权
}
}
for(int i=1;i<=n;i++){
dijkstra(i);//以每个点为源点跑一遍dijkstra
long long ans=0;
for(int j=1;j<=n;j++){//记录答案
if(dis[j]==INF)ans+=j*1ll*INF;
else ans+=j*1ll*(dis[j]+(dis1[j]-dis1[i]));
}
cout<<ans<<endl;
}
return 0;
}
单源最短路
P3371 【模板】单源最短路径(弱化版)
P4779 【模板】单源最短路径(标准版)
0-1 BFS
0-1 BFS通常是维护一个无权图的最短路。它是无权图中最高效的最短路算法。
以下内容来源于CF日报,我只是将其翻译并加以优化。
问题:
有一个具有 $V $个顶点和 \(E\) 条边的图 \(G\)。该图是一个加权图,但权重有一个限制,即它们只能是 \(0\) 或 \(1\)。编写一个高效的代码来计算来自给定源的最短路径。
解决方案:
朴素解——dijkstra算法。
这在其最佳实现中具有 \(\mathcal{O}(E+V\log V)\) 的复杂性。你可以尝试试探法,但最坏的情况仍然是一样的。在这一点上,你可能会考虑如何优化dijkstra,或者为什么我要写一个如此高效的算法作为天真的解决方案?
首先,有效的解决方案不是dijkstra的优化。其次,这是一个天真的解决方案,因为几乎每个人第一次看到这样的问题时都会编码,假设他们知道dijkstra的算法。
假设dijkstra的算法是你最好的代码,我想向你展示一个非常简单但优雅的技巧,用广度优先搜索(BFS)来解决这类图上的问题。
在我们深入研究算法之前,需要一个引理,以便稍后将事情弄清楚。
在BFS的执行过程中,包含顶点的队列最多只包含BFS树的两个连续级别的元素。
说明:BFS树是在任何图上执行BFS期间建立的树。这个引理是真的,因为在BFS执行的每个点上,我们只遍历到一个顶点的相邻顶点,因此队列中的每个顶点与队列中的所有其他顶点最多相距一级。
让我们从 0-1 BFS开始吧。
0-1 BFS:
之所以如此命名,是因为它适用于边权重为 \(0\) 和 \(1\) 的图。让我们以BFS的执行点为例,当你在一个具有权重为 \(0\) 和 \(1\) 的边的任意顶点 \(u\) 上时。与dijkstra类似,只有当一个顶点被前一个顶点松弛时,我们才会将其放入队列中(通过在该边上移动来减少距离),并且我们还保持队列在每个时间点按与源的距离排序。
现在,当我们在 \(u\) 时,我们确信一件事:沿着边 \((u,v)\) 移动将确保 \(v\) 与 \(u\) 处于同一水平或处于下一个连续水平。这是因为边权重分别为 \(0\) 和 \(1\)。边缘权重为 \(0\) 意味着它们位于同一水平上,而边缘权重为 \(1\) 意味着它们处于下面的水平上。我们还知道,在BFS期间,我们的队列最多保持两个连续级别的顶点。因此,当我们处于顶点 \(u\) 时,我们的队列包含级别 \(L_u\) 或 \(L_u+1\) 的元素。
我们还知道,对于边 \((u,v)\),\(L_v\) 要么是 \(L_u\),要么是 \(L_u+1\)。因此,如果顶点 \(v\) 是松弛的,并且具有相同的级别,我们可以将其推到队列的前面,如果它具有下一级别,我们也可以将其推向队列的末尾。这有助于我们按级别对队列进行排序,以便BFS正常工作。
但是,使用普通的队列数据结构,我们不能插入并保持它在 \(\mathcal{O}(1)\) 的时间内排序。使用优先队列会花费我们 \(\mathcal{O}(\log N)\)来保持它的排序。普通队列的问题是缺少帮助我们执行所有这些功能的方法:
-
移除顶部元素(为BFS获取顶点)
-
在开始处插入(推动具有相同级别的顶点)
-
在末尾插入(将顶点推到下一级)
双端队列(C++ STL deque)直接优化。让我们来看看这个优化的伪代码:
for all v in vertices:
dist[v] = inf
dist[source] = 0;
deque d
d.push_front(source)
while d.empty() == false:
vertex = get front element and pop as in BFS.
for all edges e of form (vertex , u):
if travelling e relaxes distance to u:
relax dist[u]
if e.weight = 1:
d.push_back(u)
else:
d.push_front(u)
正如你所看到的,这与BFS+dijkstra非常相似。但这个代码的时间复杂度是 \(\mathcal{O}(E+V)\),它是线性的,比dijkstra更有效。正确性的分析和证明也与BFS相同。
在着手解决在线评测的问题之前,请尝试以下练习,以确保您完全理解0-1 BFS的工作原理和方式:
如果我们的边权只能是 \(0\) 和 \(x(x\ge 0)\),或 \(x\) 和 \(x+1(x\ge 0)\),或 \(x\) 和 \(y(x,y\ge 0)\),我们能应用同样的技巧吗?
这个技巧其实很简单,但知道这个的人不多。
Ford
思想
该算法的核心思想很简单,对于图中的每条边\(u->v\),可以进行松弛操作让\(dis[v]\)更小,则更新。
如果图中没有负环只进行\(n-1\)轮就足够了,为什么?
每轮最少会把起点到每个点的最短路的边的数量多\(1\),比如上一轮\(dis[u]\)是由两条边组合起来的,如果这一轮\(dis[u]\)要更新,则这一轮的\(dis[u]\)最少也是由3条边组合起来的。
由于最短路的性质:不超过\(n-1\)条边,所以更新\(n-1\)次后绝对就能求出每个点的\(dis\)值。
同时,正是因为这个性质,我们可以在\(n-1\)轮后再跑一轮,若还有边能松弛,则代表出现负环。
代码
int n,m;
int road[N][N];
int dis[N];
void BellmanFord(){
memset(dis,0x3f,sizeof(dis));
dis[1]=0;
for(int i=1;i<=n;i++){
int flag=0;
for(int j=1;j<=m;j++){
if(dis[j]>dis[i]+road[i][j]){
dis[j]=dis[i]+road[i][j];
flag=1;
}
}
if(!flah)break;
}
}//必须邻接矩阵存边
时间复杂度:\(O(NM)\)
空间复杂度:\(O(N^2)\)
SPFA
它死了
思想
这里我们可以用一种类似广搜的思想来优化Bellman-Ford算法,因为很多时候我们并不需要那么多无用的松弛操作。
显然,只有上一次被松弛的结点,所连接的边的点,才有可能引起下一次的松弛操作。那么我们用队列来维护哪些结点可能会引起松弛操作,就能只访问必要的边了。
代码
int spfa(int x,int y){
memset(b,0,sizeof(b));
for(int i=0;i<=n;i++)dis[i]=1e18;
queue<int>q;
q.push(x);
b[x]=1;
dis[x]=0;
while(!q.empty()){
int u=q.front();
q.pop();
b[u]=0;
for(int i=0;i<v[u].size();i++){
int a=v[u][i].to,s=v[u][i].len;
if(dis[u]+s<dis[a]){
dis[a]=dis[u]+s;
if(!b[a]){
b[a]=1;
q.push(a);
}
}
}
}
return dis[y];
}
时间复杂度:\(O(kN)\)
空间复杂度:\(O(N)\)
Dijkstra(堆优化)
思想
松弛:如果有一条边起点\(y\)终点\(z\)权值\(v\),我们算出
\(dis[y]+v\)与\(dis[z]\)比较,如果小则执行\(dis[z]=dis[y]+v\)
第一轮
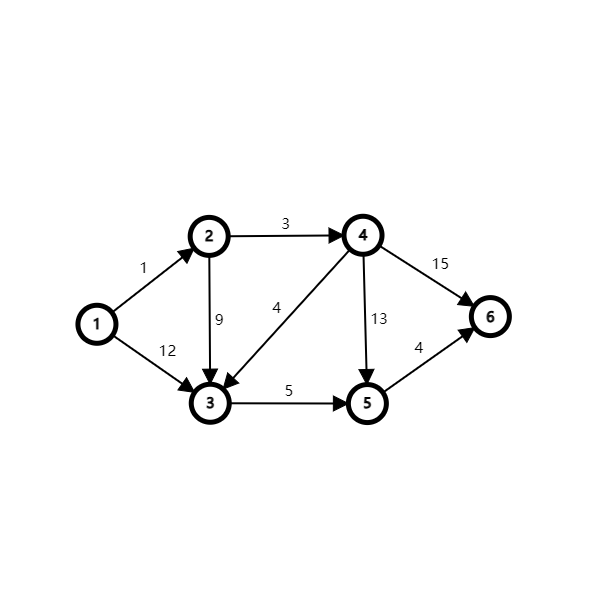
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| dis | 0 | $\infty $ | $\infty $ | $\infty $ | $\infty $ | $\infty $ |
我们在未更新点集合\(\{1,2,3,4,5,6\}\)中拿出了节点\(1\),因为\(dis[1]\)在剩下的这些点的\(dis\)值中是最小的,则现在已更新集合是\({1}\),未更新集合是\(\{2,3,4,5,6\}\)。之后我们对于1为起点的两条边,\(1->2\)和\(1->3\)进行松弛操作。
对于\(1->2\)这条边,权值为\(1\),我们发现\(dis[1]+1=1\)是小于\(dis[2]\)的,于是我们更新\(dis[2]\)。对于\(1->3\)这条边,权值为\(12\),我们发现\(dis[1]+12=12\)是小于\(dis[3]\)的,于是我们更新\(dis[3]\)。
第二轮

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| dis | 0 | 1 | 12 | $\infty $ | $\infty $ | $\infty $ |
我们在未更新点集合\(\{2,3,4,5,6\}\)中拿出了节点\(2\),因为\(dis[2]\)在剩下的这些点的\(dis\)值中是最小的,那现在已更新集合是\({1,2}\),未更新集合是\(\{3,4,5,6\}\)。之后我们对于\(2\)为起点的两条边,\(2->4\)和\(2->3\)进行松弛操作。
对于\(2->4\)这条边,权值为\(3\),我们发现\(dis[2]+3=4\)是小于\(dis[4]\)的,于是我们更新\(dis[4]\)。对于\(2->3\)这条边,权值为\(9\),我们发现\(dis[1]+9=10\)是小于\(dis[3]\)的,于是我们更新\(dis[3]\)。
第三轮

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| dis | 0 | 1 | 10 | 4 | $\infty $ | $\infty $ |
我们在未更新点集合\(\{3,4,5,6\}\)
中拿出了节点\(4\),因为\(dis[4]\)在剩下的这些点的\(dis\)值中是最小的,那现在已更新集合是\(\{1,2,4\}\),未更新集合是\(\{3,5,6\}\)。之后我们对于4为起点的三条边,\(4->3\)和\(4->5\)和\(4->6\)进行松弛操作。对于\(4->3\)这条边,权值为\(4\),我们发现\(dis[4]+4=8\)是小于\(dis[3]\)的,于是我们更新\(dis[3]\)。
对于\(4->5\)这条边,权值为\(13\),我们发现\(dis[4]+13=17\)是小于\(dis[5]\)的,于是我们更新\(dis[5]\)。对于\(4->6\)这条边,权值为\(15\),我们发现\(dis[4]+15=19\)是小于\(dis[6]\)的,于是我们更新\(dis[6]\)。
。。。
第六轮

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| dis | 0 | 1 | 8 | 4 | 13 | 17 |
我们在未更新点集合\(\{6\}\)中拿出了节点\(6\),因为\(dis[6]\)在剩下的这些点的\(dis\)值中是最小的,那现在已更新集合是\(\{1,2,3,4,5,6\}\),未更新集合为空。
之后我们发现\(6\)没有出边,结束了。现在的\(dis\)数组就是我们想要的结果。
结果

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| dis | 0 | 1 | 8 | 4 | 13 | 17 |
重复这些操作:
- 从未更新节点集合中,选取一个\(dis[i]\)最小的结点\(y\),移到已更新集合中(即让\(vis[y]=1\))。
- 对于\(y\),我们对于每条以y为起点的边执行松弛操作。
代码
struct dj{
int dis,bb;
bool operator < (const dj &a) const{
return a.dis<dis;
}
};
void dijkstra(){
priority_queue<dj>q;
for(int i=1;i<=n;i++)dis[i]=1e18;
dis[1]=0;
q.push((dj){0,1});
while(!q.empty()){
dj now=q.top();
q.pop();
if(vis[now.bb])continue;
vis[now.bb]=true;
for(int i=0;i<v[now.bb].size();i++){
if(dis[v[now.bb][i].to]>dis[now.bb]+v[now.bb][i].len){
dis[v[now.bb][i].to]=dis[now.bb]+v[now.bb][i].len;
q.push((dj){dis[v[now.bb][i].to],v[now.bb][i].to});
}
}
}
}
时间复杂度:\(O(MlogM)\)
空间复杂度:\(O(N)\)
全代码
点击查看代码
SPFA会被卡,只能用dij
#include<bits/stdc++.h>
#define int long long
using namespace std;
int dis[100100],n,m,k;
bool vis[100100]={0};
struct edge{
int to,len;
};
vector<edge>v[100100];
struct dj{
int dis,bb;
bool operator < (const dj &a) const{
return a.dis<dis;
}
};
void dijkstra(){
priority_queue<dj>q;
for(int i=1;i<=n;i++)dis[i]=1e18;
dis[k]=0;
q.push((dj){0,k});
while(!q.empty()){
dj now=q.top();
q.pop();
if(vis[now.bb])continue;
vis[now.bb]=true;
for(int i=0;i<v[now.bb].size();i++){
if(dis[v[now.bb][i].to]>dis[now.bb]+v[now.bb][i].len){
dis[v[now.bb][i].to]=dis[now.bb]+v[now.bb][i].len;
q.push((dj){dis[v[now.bb][i].to],v[now.bb][i].to});
}
}
}
}
signed main(){
cin>>n>>m>>k;
for(int i=1;i<=m;i++){
int f,x,y,s;
cin>>x>>y>>s;
v[x].push_back(edge{y,s});
//v[y].push_back(edge{x,s});
}
dijkstra();
for(int i=1;i<=n;i++){
if(dis[i]==1e18){
cout<<2147483647<<" ";
continue;
}
cout<<dis[i]<<" ";
}
return 0;
}
最短路总结
综合题1
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,b1[114514]={0},vis[114514]={0},dis[114514]={0},base[114514]={0};
int x1,y11;
struct edge{
int to,len;
};
vector<edge>v[114514],fv[114514];
void bfs(int x){
queue<int>q;
q.push(x);
b1[x]=1;
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<fv[u].size();i++){
int a=fv[u][i].to;
if(!b1[a]){
b1[a]=1;
q.push(a);
}
}
}
}//终点用反向边扩散并记录哪些点与终点联通
struct dj{
int dis,bb;
bool operator < (const dj &a) const{
return a.dis<dis;
}
};
void dijkstra(int x){
priority_queue<dj>q;
for(int i=1;i<=n;i++)dis[i]=1e9;
dis[x]=0;
q.push((dj){0,x});
while(!q.empty()){
dj now=q.top();
q.pop();
if(vis[now.bb])continue;
vis[now.bb]=true;
for(int i=0;i<v[now.bb].size();i++){
if(dis[v[now.bb][i].to]>dis[now.bb]+v[now.bb][i].len&&base[v[now.bb][i].to]){//加一个条件——此点是否可走(base[])
dis[v[now.bb][i].to]=dis[now.bb]+v[now.bb][i].len;
q.push((dj){dis[v[now.bb][i].to],v[now.bb][i].to});
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int l,r;
cin>>l>>r;
v[l].push_back(edge{r,1});
fv[r].push_back(edge{l,1});//反向建边
}
cin>>x1>>y11;
bfs(y11);//每个点是否与终点联通
for(int i=1;i<=n;i++){//每个点是否满足每条出边所指向的点都与终点连通
for(int j=0;j<v[i].size();j++){
int a=v[i][j].to;
if(!b1[a]){
goto FLAG;
}
}
base[i]=1;
FLAG:;
}
dijkstra(x1);//最短路
int ams=dis[y11];
if(ams!=1e9)cout<<ams;
else cout<<-1;
return 0;
}
差分约束
SPFA
差分约束用于判断负环
负环指的是一个图中存在一个环,里面包含的边的边权总和<0。在存在负环的图中求不出最短路径(因为只要不停走这个环,最短路径就会越来越小)。
P3385 【模板】负环(多测不清空,亲人两行泪)
#include<bits/stdc++.h>
#define int long long
using namespace std;
int dis[500010],cnt[500010],n,m,T;
bool b[500010]={0};
struct edge{
int a,s;
};
vector<edge>v[10010];
bool SPFA(int ff){
queue<int>q;
for(int i=0;i<=n;i++){
dis[i]=1e9;
cnt[i]=0;
b[i]=0;
}
q.push(ff);
b[ff]=1;
dis[ff]=0;
cnt[ff]++;
while(!q.empty()){
int u=q.front();
q.pop();
b[u]=0;
for(int i=0;i<v[u].size();i++){
int a=v[u][i].a,s=v[u][i].s;
if(dis[a]>dis[u]+s){
dis[a]=dis[u]+s;
if(!b[a]){
b[a]=1;
q.push(a);
cnt[a]++;
if(cnt[a]>n){
return 0;
}
}
}
}
}
return 1;
}
signed main(){
cin>>T;
while(T--){
cin>>n>>m;
for(int i=0;i<=n;i++)v[i].clear();
for(int i=1;i<=m;i++){
int f,x,y,s;
cin>>x>>y>>s;
if(s<0){
v[x].push_back(edge{y,s});
}else{
v[x].push_back(edge{y,s});
v[y].push_back(edge{x,s});
}
}
int l=SPFA(1);
if(!l)cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
差分约束也可以判断一些有关元素差的不等式能否全部满足
可以将不等式转化为:
- \(a_{i}-a_{j}\ge c\) \(~~\) --> \(~~\)\(a_{j}\le a_{i}-c\)
- \(a_{i}-a_{j}\le c\) \(~~\) --> \(~~\)\(a_{i}\le a_{j}+c\)
- \(a_{i}=a_{j}\) \(~~~~~~~~~\)--> \(~~\)\(a_{i}\le a_{j}+0\) && \(a_{j}\le a_{i}+0\)
我们再新建一个 \(0\) 号点,从 \(0\) 号点向其他所有点连一条权值为 \(0\) 的边。
然后以 \(0\) 号点为起点,用SPFA 跑最短路。如果有负权环,差分约束系统无解。
这个 \(0\) 号点其实就是我们所说的超级源点。
P1993 小 K 的农场
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int dis[10010],cnt[10010],n,m;
bool b[10010]={0};
struct edge{
int a,s;
};
vector<edge>v[10010];
bool SPFA(int ff){
queue<int>q;
for(int i=0;i<=n;i++)dis[i]=1e9;
q.push(ff);
b[ff]=1;
dis[ff]=0;
cnt[ff]++;
while(!q.empty()){
int u=q.front();
q.pop();
b[u]=0;
for(int i=0;i<v[u].size();i++){
int a=v[u][i].a,s=v[u][i].s;
if(dis[a]>dis[u]+s){
dis[a]=dis[u]+s;
if(!b[a]){
b[a]=1;
q.push(a);
cnt[a]++;
if(cnt[a]>n){
return 0;
}
}
}
}
}
return 1;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int f,x,y,s;
cin>>f>>x>>y;
if(f==1){
cin>>s;
v[x].push_back(edge{y,-s});
}if(f==2){
cin>>s;
v[y].push_back(edge{x,s});
}if(f==3){
v[x].push_back(edge{y,0});
v[y].push_back(edge{x,0});
}
}
for(int i=1;i<=n;i++)v[n+1].push_back(edge{i,0});
int l=SPFA(n+1);
if(l)cout<<"Yes";
else cout<<"No";
return 0;
}
P1260 工程规划输出最短路即可(双倍经验)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int dis[10010],cnt[10010],n,m;
bool b[10010]={0};
struct edge{
int a,s;
};
vector<edge>v[10010];
bool SPFA(int ff){
queue<int>q;
for(int i=0;i<=n;i++)dis[i]=1e9;
q.push(ff);
dis[ff]=0;
cnt[ff]=1;
b[ff]=1;
while(!q.empty()){
int a=q.front();
q.pop();
b[a]=0;
for(int i=0;i<v[a].size();i++){
int u=v[a][i].a,w=v[a][i].s;
if(dis[u]>dis[a]+w){
dis[u]=dis[a]+w;
if(!b[u]){
b[u]=1;
q.push(u);
cnt[u]++;
if(cnt[u]>n)return 0;
}
}
}
}
return 1;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y,s;
cin>>x>>y>>s;
v[x].push_back(edge{y,s});
}
for(int i=1;i<=n;i++)v[0].push_back(edge{i,0});
int l=SPFA(0);
if(l){
for(int i=1;i<=n;i++)cout<<-1*dis[i]<<endl;
}else cout<<"NO SOLUTION";
return 0;
}
树
树基础
我们可以将树看作一个有从属关系的结构,除了最顶上的点(根节点),每个 点都有一个“上级”(父亲节点)。假设树中有 \(n\) 个点,则这 \(n\) 个点是由 \(n-1\) 条边连起来的。 为实现父亲节点与子节点的互通信息,树是一个无向图。
层数(节点的深度):如果我们把根节点看作 第 00 层,则第 kk 层的点就是从根节点出发要往 下刚好走 kk 步能到达的点。形式化地,每个节点地深度为它父亲的深度加 11。根节点深度为 00。
树的高度:所有点中深度的最大值。
一个没有固定根结点的树称为无根树。
在无根树的基础上,指定一个结点称为 根(一般为 \(1\)),则形成一棵 有根树。
子树:删掉与父亲相连的边后,该结点所在的子图。
叶子结点:没有子结点的结点。
以下面的树为例:
\(1\) 为根节点,\(4\) 是 \(7\) 的父亲,\(5,6\) 是 \(3\) 的儿子,\(5,6\) 是兄弟节点,\(2,5,6,7\) 是叶子节点,若根节点深度为 \(0\),则 \(5\) 深度为 \(2\),树的高度为 \(2\)。
特殊的树
点的度数:该点的子节点个数。
\(k\) 叉树:每个点的最大度数为 \(k\),一般我们
处理二叉树比较多。
满二叉树:每个非叶子节点的节点有\(2\)个子节点。
完全二叉树:一棵深度为 \(k\) 的有 \(n\) 个节点的
二叉树,对树中的节点按从上至下、从左到右
的顺序进行编号,如果编号为 $ i ( 1 \le i \le n ) $的
节点与满二叉树中编号为 \(i\) 的节点在二叉树中
的位置相同,则这棵二叉树称为完全二叉树。
树的实现
- 我们可以储存点的权值,父亲和儿子。
struct node{
int v,fa,son[114514];
}tree[114514];
- 对于二叉树,我们也可以对点编号,根节点编号为 \(1\),点 \(i\) 的父亲为点 \(\dfrac{i}{2}\),左儿子为点 \(2i\),右儿子为点 \((2i+1)\)。可 \(O(1)\) 查询父亲/儿子。
树上 DFS
记录上一节点,根节点上一节点为0或-1。
每次找儿子时判断有没有走回上一节点即可。
inline void dfs(int x,int las){
for(int i=0;i<v[x].size();i++){
if(v[x][i]==las)continue;
dfs(v[x][i],x);
}
}
二叉树的遍历
先序遍历:根->左子树->右子树
中序遍历:左子树->根->右子树
后序遍历:左子树->右子树->根
递归处理子树。
堆/优先队列
堆是一种两个儿子都大于等于/小于等于父亲的完全二叉树。
树根一般存的是最值。
大多数情况下无需手写,已用 STL 中的 priority_queue 做了类似操作的封装。(详见)
时间复杂度:插入 \(O(\log_2n)\),查询极值 \(O(1)\),删除极值 \(O(\log_2n)\),删除任意值 \(O(\log_2n)\)(手写堆)。
表达式树
emm...太长了
我们把所有数字存为叶子节点,在前/后序遍历即可。
如4*3-6/3
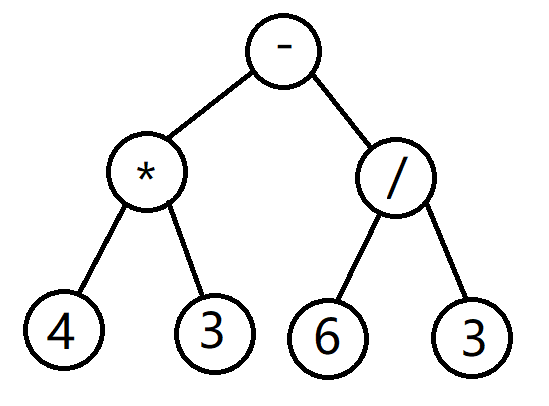
前序遍历为:- * 4 3 / 6 3(前缀表达式)
后序遍历为:4 3 * 6 3 / -(后缀表达式)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s;
int k[10001],u0;
int us;
stack<char>st;
vector<char>v[10001];
vector<char>tree1[40001];
vector<char>hz;
struct tree{
int l,r;
int sum,tag;
}t[40010];
void builds(int x,int l,int r){
t[x].l=l,t[x].r=r;
if(l==r){
t[x].sum=0;
return;
}
int mid=(l+r)>>1;
builds(x*2,l,mid);
builds(x*2+1,mid+1,r);
t[x].sum=t[x*2].sum+t[x*2+1].sum;
}
void down(int x){
if(t[x].tag){
t[x*2].tag+=t[x].tag;
t[x*2+1].tag+=t[x].tag;
t[x*2].sum+=(t[x*2].r-t[x*2].l+1)*t[x].tag;
t[x*2+1].sum+=(t[x*2+1].r-t[x*2+1].l+1)*t[x].tag;
t[x].tag=0;
}
}
void change(int x,int l,int r,int a){
if(t[x].l>=l&&t[x].r<=r){
t[x].tag+=a;
t[x].sum+=(t[x].r-t[x].l+1)*a;
return;
}
if(t[x].l==t[x].r)return;
down(x);
int mid=(t[x].l+t[x].r)>>1;
if(mid>=l)change(x*2,l,r,a);
if(mid<r)change(x*2+1,l,r,a);
t[x].sum=t[x*2].sum+t[x*2+1].sum;
}
int ask(int x,int l,int r){
if(l<=t[x].l&&r>=t[x].r)return t[x].sum;
down(x);
int mid=(t[x].l+t[x].r)>>1;
int sum=0;
if(mid>=l)sum+=ask(x*2,l,r);
if(mid<r)sum+=ask(x*2+1,l,r);
return sum;
}
int check(char c){
switch(c){
case '+':return 1;
case '-':return 2;
case '*':return 3;
case '/':return 3;
case '^':return 4;
case '(':return 0;
case ')':return 0;
default:return 1e9;
}
}
int suan(char c,int x,int y){
switch(c){
case '+':return x+y;
case '-':return x-y;
case '*':return x*y;
case '/':return x/y;
case '^':return pow(x,y);
default:return -1e9;
}
}
void build(int l,int r,int x){
builds(1,l,r);
if(v[l][0]=='('&&v[r][0]==')')l++,r--;
if(l+v[l].size()-1==r){
tree1[x]=v[l];
return;
}
stack<int>st;
for(int i=l;i<=r;i+=v[i].size()){
if(v[i][0]=='('){
st.push(i);
}
if(v[i][0]==')'){
int la=st.top();
st.pop();
change(1,la,i,1);
}
}
int maxf=1e9,maxn;
for(int i=l;i<=r;i+=v[i].size()){
int uo=check(v[i][0]);
int ck=!ask(1,i,i);
if(uo<maxf&&ck){
maxf=uo;
maxn=i;
}
}
tree1[x]=v[maxn];
build(l,maxn-1,x*2);
build(maxn+1,r,x*2+1);
}
void found(int x){
if(x>=us)return;
found(x*2);
found(x*2+1);
for(int i=0;i<tree1[x].size();i++){
hz.push_back(tree1[x][i]);
}
}
signed main(){
cin>>s;
for(int i=0;i<s.size();i++){
if(s[i]>='0'&&s[i]<='9'){
while(s[i]>='0'&&s[i]<='9'){
v[i].push_back(s[i]);
i++;
}
i--;
}
else{
v[i].push_back(s[i]);
}
}
u0=s.size()-1;
us=1<<u0;
build(0,u0,1);
found(1);
for(int i=0;i<hz.size();i++)cout<<hz[i]<<" ";
return 0;
}
/*
8-(3+2*6)/5+4
*/

 图论打砸会
图论打砸会

 浙公网安备 33010602011771号
浙公网安备 33010602011771号