树状数组学习笔记

树状数组简介

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。
——百度百科

前置知识：lowbit

lowbit是指一个数最低位的 \(1\)

  • \(4=(100)_2\) -> \(lowbit(100)=(100)_2=4\) 即 \(lowbit(4)=4\)
  • \(6=(110)_2\) -> \(lowbit(110)=(10)_2=2\) 即 \(lowbit(6)=2\)
  • \(7=(111)_2\) -> \(lowbit(111)=(1)_2=1\) 即 \(lowbit(7)=1\)

树状数组

树状数组是一个可以快速处理前缀信息的数据结构

树状数组一般使用数组进行存储，数组中 \(x\) 号节点，存储的是区间 \([x−lowbit(x)+1,x]\) 的信息和，利用这
一点可以在线性时间内建出树状数组），也可以实现全局的第 \(k\) 小查询，其中 \(tree[x]\) 表示 \(\sum_{{i=x-lownit(x)+1}}^x a_i\)

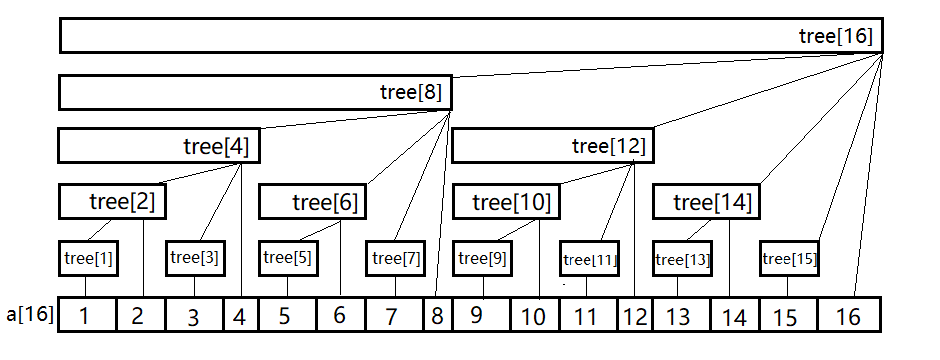
image

\[\scriptsize\color{grey}{树状数组} \]

树状数组特性：

  • 每个内部节点 \(tree[x]\) 保存以它为根的所有叶子节点的和
  • 每个内部节点 \(tree[x]\) 的子节点数等于 \(lowbit(x)\) 的位数
  • 每个内部节点 \(tree[x]\) 的父节点是 \(tree[x+lowbit(x)]\)
  • 树的深度为 \(logn\)

树状数组实现

1.建树

直接用加点函数循环

int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点赋值，所有祖先节点都增加（与前缀和一样）
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}

调用入口：

for(int i=1;i<=n;i++){//点得一个一个加
	cin>>a[i];
	add(i,a[i]);
}

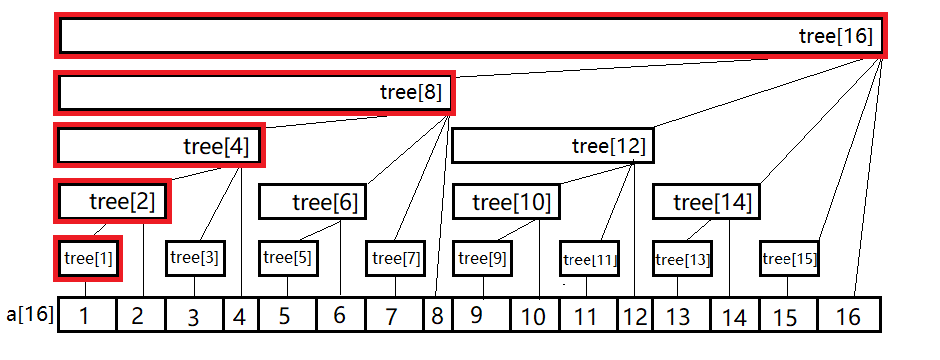
2.单点修改

修改函数与上面建树函数相同
我们如果更改点 \(1\) ，需要更改的节点如图红圈部分：
image

\[\scriptsize\color{grey}{更改点1} \]

int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点同所有祖先节点都增加
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}

调用入口：add(x,a);

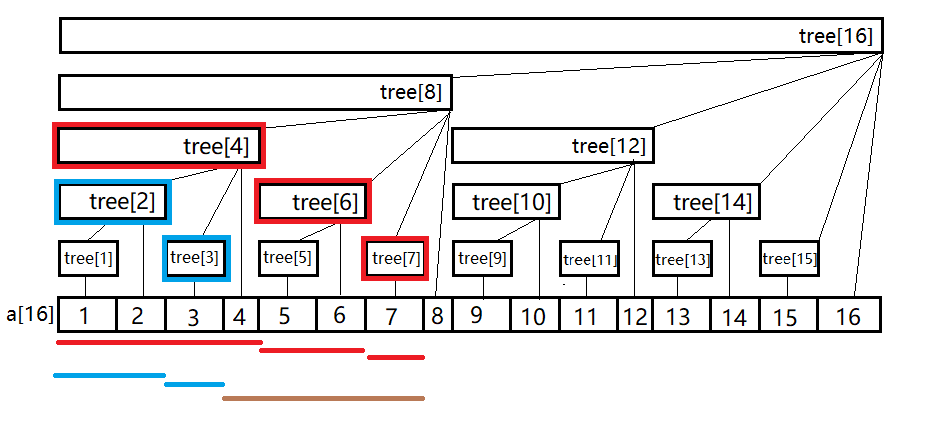
3.查询

我们如果查询区间 \([4,7]\) ，先求出区间 \([1,7]\) (红色线段表示)和区间 \([1,3]\) (蓝色线段表示)再相减（绿色线段表示），需要计算的节点如图红圈（ 区间 \([1,7]\) 需要计算的节点）及蓝圈（ 区间 \([1,3]\) 需要计算的节点）部分：
image

\[\scriptsize\color{grey}{查询区间[4,7]} \]

int ask(int x){
	int val=0;
	while(x>0){
		val+=t[x];//求出1-x的值
		x-=x&-x;//与x=x-lowbit(x)等价	
	}
	return val;//返回答案
}

调用入口：ask(r)-ask(l-1);

单点查询要借助区间查询，如果信息支持区间差的话，可以用 \([1, y]\) 的值减去 \([1, y − 1]\) 的值

int ask(int x){
	int val=0;
	while(x>0){
		val+=t[x];//求出1-x的值
		x-=x&-x;//与x=x-lowbit(x)等价	
	}
	return val;//返回答案
}

调用入口：ask(x)-ask(x-1);

4.区间修改

区间修改得更改很多地方

建树

int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点赋值，所有祖先节点都增加（与前缀和一样）
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}

调用入口：

for(int i=1;i<=n;i++){//点得一个一个加
	cin>>a[i];
	add(i,a[i]-a[i-1]);
}

修改

int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点同所有祖先节点都增加
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}

调用入口：

add(l,k);
add(r+1,-k);

如果修改单点则把 \(l,r\) 都赋值为 \(x\)

单点查询

调用入口变为：ask(x)

区间查询

\[这个人颓废去了，N年后再更 \]

树状数组到这就结束了，练习一下吧！

例题1

luogu P3374 【模板】树状数组 1

这题可以用用树状数组单点修改，区间查询来做

点击查看题目 
#include<bits/stdc++.h> 
using namespace std;
int t[500001],a[500001],n,m;
int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点同所有祖先节点都增加
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}
int ask(int x){
	int val=0;
	while(x>0){
		val+=t[x];//求出1-x的值
		x-=x&-x;//与x=x-lowbit(x)等价	
	}
	return val;//返回答案
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){//点得一个一个加
		cin>>a[i];
		add(i,a[i]);
	}
	for(int i=1;i<=m;i++){
		int flag,x,y;
		cin>>flag>>x>>y;
		if(flag==1){
			add(x,y);//增加y
		}else{
			cout<<ask(y)-ask(x-1)<<endl;//输出区间[x,y]的值
		}
	}
	return 0;
}

例题2

luogu P3368 【模板】树状数组 2

这题可以用用树状数组区间修改，单点查询来做

点击查看题目 
#include<bits/stdc++.h> 
using namespace std;
int t[500001],a[500001],n,m;
int add(int x,int y){
	while(x<=n){
		t[x]+=y;//此节点同所有祖先节点都增加
		x+=x&-x;//与x=x+lowbit(x)等价	
	}
}
int ask(int x){
	int val=0;
	while(x>0){
		val+=t[x];//求出1-x的值
		x-=x&-x;//与x=x-lowbit(x)等价	
	}
	return val;//返回答案
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){//点得一个一个加
		cin>>a[i];
		add(i,a[i]-a[i-1]);
	}
	for(int i=1;i<=m;i++){
		int flag,x,y,k;
		cin>>flag>>x;
		if(flag==1){
			cin>>y>>k; 
			add(x,k);
			add(y+1,-k);//区间增加y
		}else{
			cout<<ask(x)<<endl;//输出点x的值
		}
	}
	return 0;
}

二维树状数组

先推式子

\[\sum_{i=1}^{x} \sum_{j=1}^{x}\sum_{x_1=1}^{i} \sum_{x_2=1}^{j}a_{x_1,y_1}\\ =\sum_{i=1}^{x} \sum_{j=1}^{x} a_{i,j}\times(x+1-i)\times(y+1-j)\\ =(x+1)\times(y+1)\times\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}- (y+1)\times\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times i -(x+1)\times\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times j+\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times i\times j \]

然后我们开 \(4\) 个树状数组分别记录

\[\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}(1式)，\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times i(2式)，\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times j(3式)，\sum_{i=1}^{x}\sum_{j=1}^{y}a_{i,j}\times i\times j(4式) \]

再利用二维差分实现区间修改，二维前缀和实现区间查询即可

P4514 上帝造题的七分钟

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
struct twoBIT{
	int t[2500][2500][4];
	int add(int x,int y,int z){
		int nx=x;
		while(nx<=n){
			int ny=y;
			while(ny<=m){
				t[nx][ny][0]+=z;//1式sigma
				t[nx][ny][1]+=(x-1)*z;//2式sigma
				t[nx][ny][2]+=(y-1)*z;//3式sigma
				t[nx][ny][3]+=(x-1)*(y-1)*z;//4式sigma
				ny+=ny&-ny;
			}
			nx+=nx&-nx;	
		}
	}
	int ask(int x,int y){
		int val=0;
		int nx=x;
		while(nx>0){
			int ny=y;
			while(ny>0){
				val+=t[nx][ny][0]*x*y;//1式*系数 
				val-=t[nx][ny][1]*y;//2式*系数 
				val-=t[nx][ny][2]*x;//3式*系数 
				val+=t[nx][ny][3];//4式*系数1
				ny-=ny&-ny;
			}
			nx-=nx&-nx;
		}
		return val;
	}
}t1;
signed main(){
	char c;
	cin>>c>>n>>m;
	while(cin>>c){
        if(c=='L'){
        	int l1,r1,l2,r2,x;
        	cin>>l1>>r1>>l2>>r2>>x;
        	t1.add(l1,r1,x);
        	t1.add(l1,r2+1,-x);
        	t1.add(l2+1,r1,-x);
        	t1.add(l2+1,r2+1,x);//二维差分 
		}else{
			int l,r,l1,r1;
			cin>>l>>r>>l1>>r1;
			int ans=0;
			ans=t1.ask(l1,r1);
			ans-=t1.ask(l-1,r1);
			ans-=t1.ask(l1,r-1);
			ans+=t1.ask(l-1,r-1);//二维前缀和 
			cout<<ans<<endl;
		}
    }
	return 0;
}

求逆序对

二元逆序对

P1908 逆序对

排序后记录每个点原来的位置，对于每个数则加入树状数组，并求出它之前的数的数量 \(h\)，它的值即为 \(i-h\)。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
struct node{
	int a,i;
	bool operator <(const node &aa)const{
		if(a==aa.a)return i<aa.i;
		return a<aa.a;
	}
}a[1000001];
int rs[500010];
struct BIT{
	int t[500100];
	int add(int x,int y){
		while(x<=n){
			t[x]+=y;
			x+=x&-x;	
		}
	}
	int ask(int x){
		int val=0;
		while(x>0){
			val+=t[x];
			x-=x&-x;
		}
		return val;
	}
}t1;
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].a;
		a[i].i=i;
	}
	sort(a+1,a+n+1);//排序 
	for(int i=1;i<=n;i++){
		rs[a[i].i]=i;//记录每个值排序所在位置 
	}
	int ans=0;
	for(int i=1;i<=n;i++){
        t1.add(rs[i],1);//加入树状数组 
        ans+=i-t1.ask(rs[i]);//求有多少个在它之前,再反推 
    }
    cout<<ans<<endl;
	return 0;
}

三元逆序对

Enemy is weak

我们枚举中间的节点，再把前后 大于且原 \(i\) 值小于它 和 小于且原 \(i\) 值大于它 的节点数相乘即可。

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
struct node{
	int a,i;
	bool operator <(const node &aa)const{
		if(a==aa.a)return i<aa.i;
		return a<aa.a;
	}
}a[1000001];
bool cmp(node a,node aa){
	if(a.a==aa.a)return a.i<aa.i;
	return a.a>aa.a;
}
int rs[1000010],rs2[1000010];
struct BIT{
	int t[1000100];
	int add(int x,int y){
		while(x<=n){
			t[x]+=y;
			x+=x&-x;	
		}
	}
	int ask(int x){
		int val=0;
		while(x>0){
			val+=t[x];
			x-=x&-x;
		}
		return val;
	}
}t1,t2;
int l1[1000001],r1[1000001];
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].a;
		a[i].i=i;
	}
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++){
		if(a[i].a!=a[i-1].a||i==1)rs[a[i].i]=i;
		else rs[a[i].i]=rs[a[i-1].i];
	}
	int ans=0;
	for(int i=n;i>0;i--){
        l1[i]=t1.ask(rs[i]-1);
		t1.add(rs[i],1);
    }
    for(int i=1;i<=n;i++){
		r1[i]=t2.ask(n-rs[i]);
    	t2.add(n-rs[i]+1,1);
	}
	for(int i=1;i<=n;i++){
		ans+=l1[i]*r1[i];
	}
    cout<<ans<<endl;
	return 0;
}

权值树状数组

核心代码：

点击查看代码 
struct BIT{
	int t[1000100];
	int add(int x,int y){
		while(x<=n){
			t[x]+=y;
			x+=x&-x;	
		}
	}
	int kth(int k){
    	int r=0,st=0,x,y;
    	for(int i=log2(n);i>=0;i--){
    		x=r+(1<<i),y=st+t[x];
        	if(x>n)continue;
       	 	if(y<k)r=x,st=y;
    	}
    	return r+1;
	}
};
posted @ 2023-01-18 20:49  ccrui  阅读(56)  评论(0)    收藏  举报