P8404 [CCC2022 J5] Square Pool 题解

题意解释：

一个 \(n\times n\) 个点的网格图上有 \(T\) 个不能覆盖的点，求这网格图上最大的正方形的边长。

55 pts

前缀和记录，枚举边长和左上角，\(O(n^3)\) 实现。

进一步优化，加一个二分，可以达到 \(O(n^2\log n)\)，但 \(n\le 5\times 10^5\)，还是过不了！

100 pts

容易发现 \(T\) 很小，所以可以使用 \(O(T^2)\) 的方法实现

扫描左右界：

先把每一棵树按 \(y\) 坐标排序。

接下来就可以保证存数的数组 \(t\) 中树的 \(y\) 坐标具有单调性。

可以发现正方形的边长为最上面挨到的树或墙与强于最下面挨到的树或墙的距离与最左面挨到的树最上面挨到的树或墙与强于最右面挨到的树或墙的距离中的最小值。

所以说排序后我们可以枚举所有可能的上下界。每一次从一个点对应的横线作为下界开始往上枚举上界，还可以求出左右界，左右界就为过程中经过的点的 \(x\) 坐标的极差。

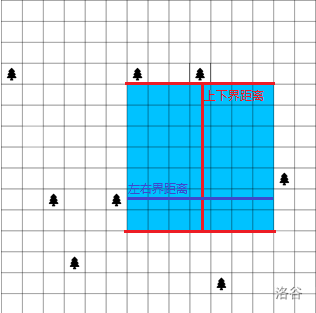
还可以加一个小优化：因为极差不会增大，所以当极差小于上下界的距离时，正方形边长就不会有增加了。

从一个点求上下界的代码如下：

int getx(int x){//上下界，x代表起始点 
	int maxx=1,minx=n+1,ans=0;
	for(int i=x+1;i<=T;i++){
		if(minx-maxx<a[i].y-a[x].y)return ans;//优化 
		ans=a[i].y-a[x].y-1;//上下界距离 
		if(a[i].x<=a[x].x){
			if(maxx<a[i].x)maxx=a[i].x;//更新极值 
		}
		if(a[i].x>=a[x].x){
			if(minx>a[i].x)minx=a[i].x;//更新极值 
		}
	}
	return ans;
}

同理我们也可以对每一棵树按 \(x\) 坐标排序，再求出左右界和上下界。

代码：

int gety(int x){//左右界，x代表起始点 
	int maxx=1,minx=n+1,ans=0;
	for(int i=x+1;i<=T;i++){
		if(minx-maxx<b[i].x-b[x].x)return ans;//优化 
		ans=b[i].x-b[x].x-1;//左右界距离 
		if(b[i].y<=b[x].y){
			if(maxx<b[i].y)maxx=b[i].y;//更新极值 
		}
		if(b[i].y>=b[x].y){
			if(minx>b[i].y)minx=b[i].y;//更新极值 
		}
	}
	return ans;
}

四个角加树：

这时我们发现样例一过不了，因为正方形的左界和下界都是靠墙的，这时我们可以在地图的左下角的左下角、右下角的右下角、左上角的左上角、右上角的右上角分别加一棵树，如图。

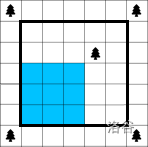
这样方形的边界也可以是院子的四面墙了。

四棵树的位置分别为 \((0,0),(n+1,0),(0,n+1),(n+1,n+1)\)。

代码：

---

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,T;
struct dot{
	int x,y;
}a[114],b[114];
bool cmpx(dot x,dot y){
	if(x.x==y.x)return x.y<y.y;
	else return x.x<y.x;
}
bool cmpy(dot x,dot y){
	if(x.y==y.y)return x.x<y.x;
	else return x.y<y.y;
}
int getx(int x){//上下界 
	int maxx=1,minx=n+1,ans=0;
	for(int i=x+1;i<=T;i++){
		if(minx-maxx<a[i].y-a[x].y)return ans;//优化 
		ans=a[i].y-a[x].y-1;//上下界距离 
		if(a[i].x<=a[x].x){
			if(maxx<a[i].x)maxx=a[i].x;//更新极值 
		}
		if(a[i].x>=a[x].x){
			if(minx>a[i].x)minx=a[i].x;//更新极值 
		}
	}
	return ans;
}
int gety(int x){//左右界 
	int maxx=1,minx=n+1,ans=0;
	for(int i=x+1;i<=T;i++){
		if(minx-maxx<b[i].x-b[x].x)return ans;//优化 
		ans=b[i].x-b[x].x-1;//左右界距离 
		if(b[i].y<=b[x].y){
			if(maxx<b[i].y)maxx=b[i].y;//更新极值 
		}
		if(b[i].y>=b[x].y){
			if(minx>b[i].y)minx=b[i].y;//更新极值 
		}
	}
	return ans;
}
signed main(){
    cin>>n;
	cin>>T;
    for(int i=1;i<=T;i++){
    	cin>>a[i].x>>a[i].y;
    	b[i]=a[i];
	}
	a[T+1]=dot{0,n+1};b[T+1]=a[T+1];
	a[T+2]=dot{n+1,0};b[T+2]=a[T+2];
	a[T+3]=dot{n+1,n+1};b[T+3]=a[T+3];
	a[T+4]=dot{0,0};b[T+4]=a[T+4];//四角加树 
	T+=4;
	sort(a+1,a+T+1,cmpy);//求上下界的排序 
	sort(b+1,b+T+1,cmpx);//求左右界的排序 
	int ans=0;
	for(int i=1;i<=T;i++){
		int u=max(getx(i),gety(i));
		ans=max(ans,u);
	}
	cout<<ans<<endl;
    return 0;
}