CF190B题解

题目传送门

题意理解

题目已经说的很清楚了，输出第三个圆连接两个圆的最小半径。

两圆圆心之间的距离

根据两点间的面积公式，可以求出两圆圆心之间的距离长度为：

\[\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} \]

设 \(l=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\)。

两个圆在平面上有三种状态

1.不相交

情况一

当 \(l>r_1+r_2\) 时出现。

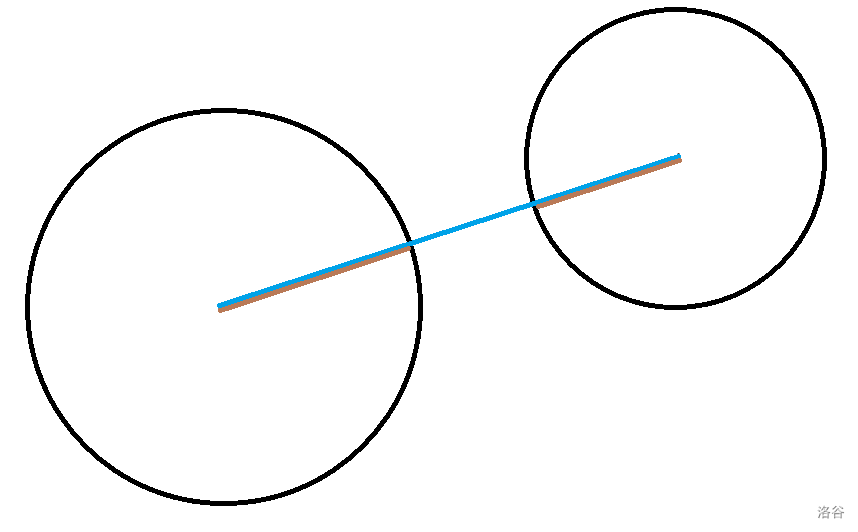
很容易发现把第三个圆放在蓝色线段是最优的，那它的直径就是两圆圆心的距离长度减去两圆半径的长度（即蓝色线段减去两段红色线段），所以第三个圆的半径就是：

\[\frac{l-r_1-r_2}{2} \]

情况二

当 $l<\left | r_1-r_2 \right | $ 时出现。

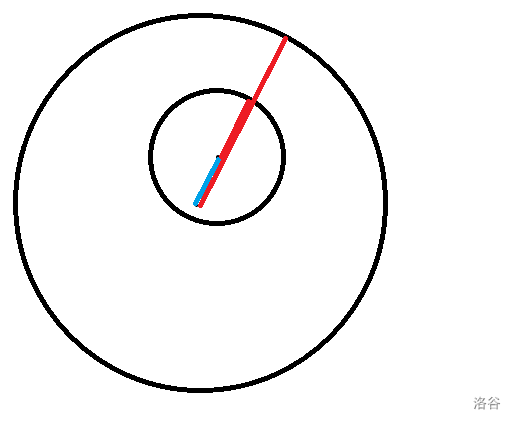
很容易发现把第三个圆放在红色线段是最优的，那它的直径就是大圆半径的长度减去两圆圆心的距离长度和小圆半径的长度之和，所以第三个圆的半径就是：

\[\frac{max_{r_1,r_2}-l-min_{r_1,r_2}}{2} \]

2.相交且不是相切

当 $l>\left | r_1-r_2 \right | $ 且 \(l<r_1+r_2\) 时出现。

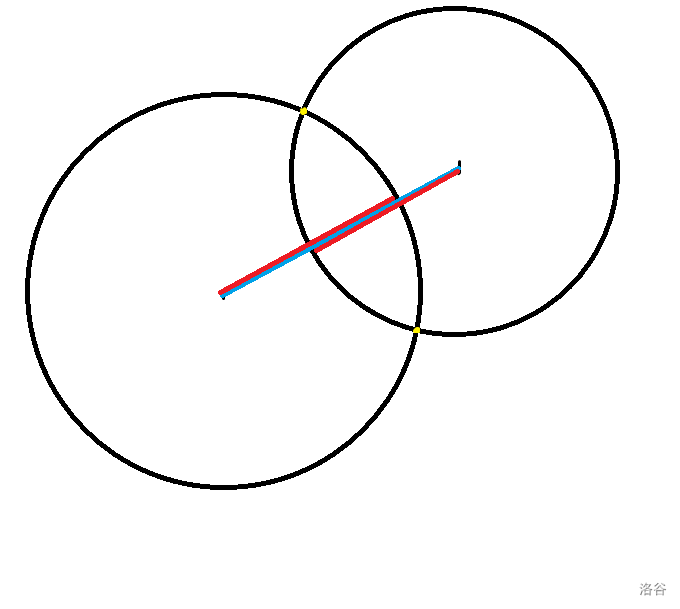
这时只要把第三个圆放在两个交点的位置，这时它的半径就可以为 \(0\) 了。

3.相切

当$l=\left | r_1-r_2 \right | $ 或 \(l=r_1+r_2\) 时出现。

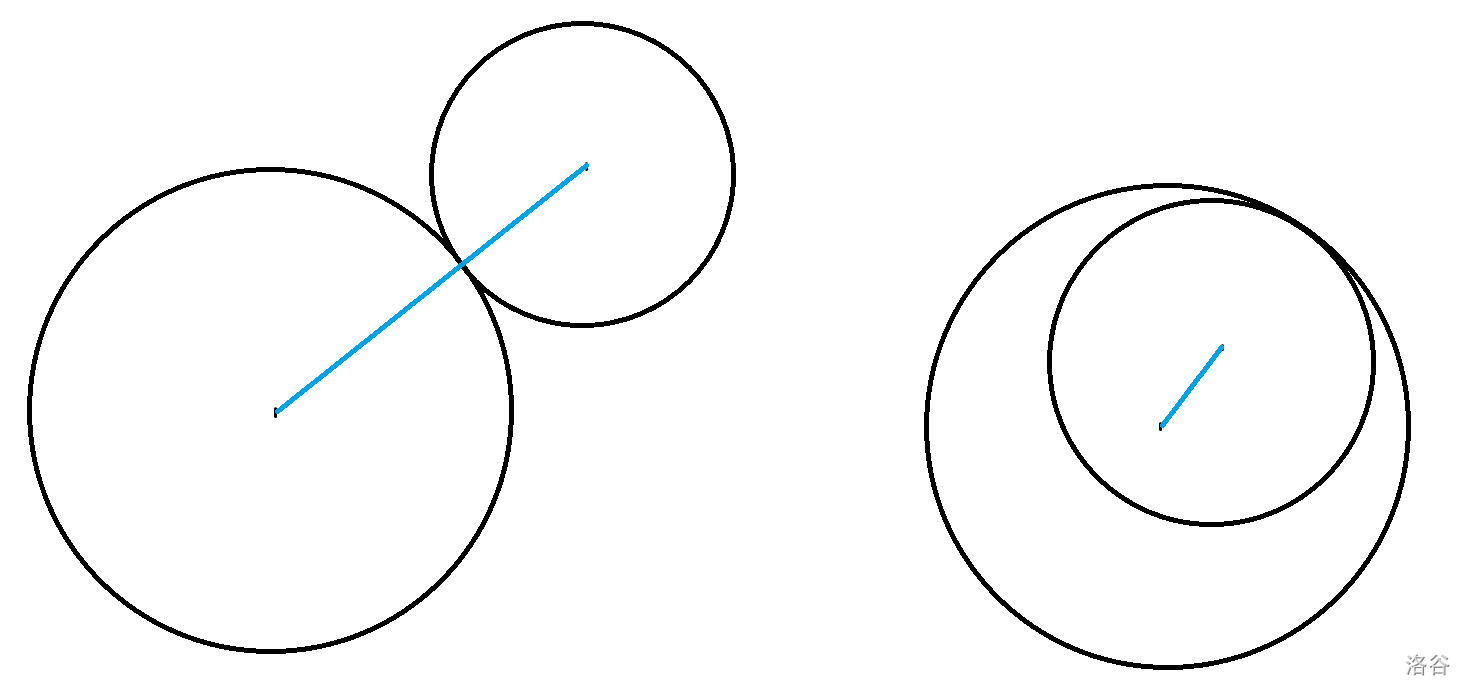
• 当出现前一种情况时，可以发现蓝色线段等于两圆半径的长度之和，
  所以满足：

\[\sqrt{(x1-x2)^2+(y1-y2)^2}=r1+r2 \]

• 当出现后一种情况时，可以发现蓝色线段等于两圆半径的长度之和，
  所以满足：

\[\sqrt{(x1-x2)^2+(y1-y2)^2}=r1-r2 \]

当出现这两种情况时直接输出 \(0\) 即可。

代码

#include<bits/stdc++.h>
using namespace std;
double x1,y,r1;
double x2,y2,r2;
int main(){
	cin>>x1>>y>>r1;
	cin>>x2>>y2>>r2;//输入 
	double xc=(x1-x2)*(x1-x2);
	double yc=(y-y2)*(y-y2);
	double l=sqrt(xc+yc),ans;//两圆圆心之间的距离长度
	if(fabs(l-abs(r1+r2))<0.0000001)cout<<"0.000000000000000";//相切情况一
	else if(fabs(l-abs(r1-r2))<0.0000001)cout<<"0.000000000000000";//相切情况二
	else if(l<r1+r2&&l>fabs(r1-r2))cout<<"0.000000000000000";//相交且不是相切 
	else if(l>r1+r2)printf("%.15lf",(l-r1-r2)/2);//不相交情况一
	else printf("%.15lf",(max(r1,r2)-l-min(r1,r2))/2);//不相交情况二
	return 0;
}

AC记录