算法第五章作业及学期总结

对回溯法理解

在我的理解中，回溯的本质其实就是穷举遍历，只不过它不是并不是真的把所有情况全部考虑一遍，它的核心在于有选择性、有思考性的遍历。

与普通的遍历不同的是，回溯法采用了树这种数据结构来进行遍历所有可能出现的结果，对于某一具体问题叫做解空间树。而这在回溯法中通常有两种——子集树和排列树。子集树就是通过对每个元素的选择与不选择2种情况构建的二叉树，树的程度就是元素的个数；排列树则是通过从根节点到叶子节点之间的不同路径，也就是不同的节点排序组合来表示不同的元素排列方式。而这两种不同的解空间树也将可用回溯法解决的问题大致分成了2种。

子集树

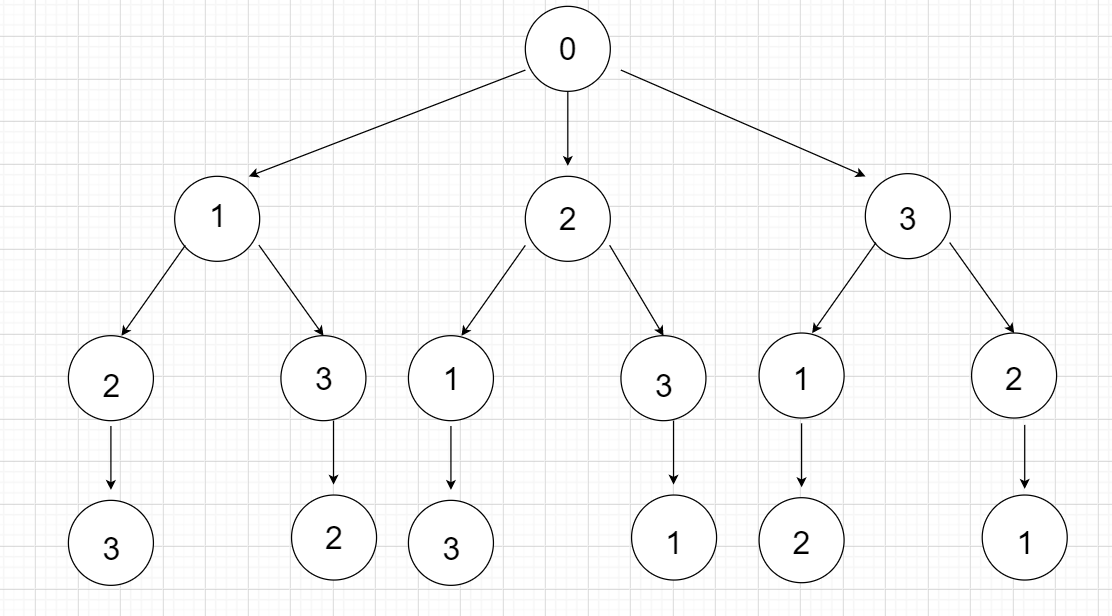
排列树

而回溯法最精髓的地方就在于其遍历的方法——“回溯”。回溯的过程便是对同一节点产生的结果进行多方向预测，通过递归的方式进入到这一个预测方向继续运行下去，而在递归后就对预测结果进行“收回”，然后再进行下一方向的预测。一般的回溯法会包括一个Backtrack函数，模板大致如下：

// 回溯函数模板
void Backtrack(int t)
{
	// 通常为限界界或剪枝，或是最终输出结果
    if (t>n)
    	return;
    
    for (int i = 1; i <= k; i++) // 不同方向的假设预测
    {
        ans += arr[i]; // 假定某种方向
        Backtrack(t + 1); // 在这方向下递归运行下去
        ans -= arr[i]; // 回溯
    }  
}

为了提高计算速度，可以采用某种策略来进行剪枝和限界，从而对于可预测范围内必不可能出现我们想要结果的解空间树的部分进行舍弃，也就是不去遍历。这大大减少了不必要的计算，减少了很多的时间开销，也就是与普通遍历先进在的地方。所以，这样一种与原来算法相比降低了很大的时间复杂度的算法就算是一个算法最大的价值所在了。

通过回溯法的解空间树结构加上分枝限界等策略，就可以解决很多需要找出最优解或者所有情况的问题，这其中包括经典的0-1背包问题。

课程的收获

这门课程和数据结构密不可分，作为一个计算机从业者，数据结构和算法一直是最最重要的基本功之一，而它也与计算机网络、操作系统、计算机组成原理并称程序员“四大件”，在面试中也具有举足轻重的作用。不少公司在招聘应届生时，往往会侧重去考数据结构与算法，而不是像社招那样去更多的考框架应用和原理或中间件技术的使用。

除了面试，在具体项目中算法也是与系统性能分不开的。简单来说，一个接口如果做了算法优化后解决问题的时间复杂度降低了一个维度，那算法算是发挥了它最大的作用。 在响应时间就是生命线的web应用来说，提高响应速度必然是开发者最重要的任务之一，除了从系统层面去考虑之外，从算法的角度去解决问题也是最主流的做法之一，也是一位优秀的程序员应具备的能力。

不会合理利用算法的程序员不是一位合格的程序员。因此，学好算法是很重要的，这门课只是起点，而不是终点。

遇到的困难

遇到的困难多是来自的题目中未通过的case，而PTA不像leetcode那样可以让用户直接看到测试用例，这无疑大大增加了debug的时间。虽然大多数都是由于边界的考虑，但也增强了自己思考问题的严谨性。不过，个人还是更倾向于leetcode这样可以快速定位到自己问题的方式。此外，也出现过由于编译器版本不同或其它来自服务端（判题机）的问题产生的困扰。但是遇到困难的解决过程是十分令人收益的，特别是在思考算法，理解算法，实现算法的整个投入的过程。

教学建议

老师讲得很好，表达清晰，用词准确，详略得当，风趣幽默。希望能保持优秀的教学水平。

欢迎关注我的个人博客：https://ccqstark.gitee.io/