一个基于反向传播的神经网络的实现
这实际上是一个叫“手写识别”项目的前传
想法来自3B1B的视频。
祭出地址~
分别是三个视频
看完以后蠢蠢欲动的我也想亲自动手,毕竟看完视频后感觉我都能看得懂啊,我也可以实现啊,于是高三的我走上了这条不归路
视频给你的一大错觉就是,内容我都好像懂了。但实际上需要理解的细节甚至是错误的理解是数不胜数的
好吧,偏执性格的我不惜自习课的宝贵时间,偷偷地。。。。咳咳,偏了偏了。
真正让我理解反向传播(或许理解了)是这篇伟大的博文。自认为这篇文章结合具体例子,削弱了公式的抽象性。
我这里想补充下具体到算法实现的细节,说明下程序是怎么跑这个算法的。 公式也是根据人家的文章推导化简而得。
现在,我有如下神经网络(上标是层数,下表是每个神经元在该层的序号)
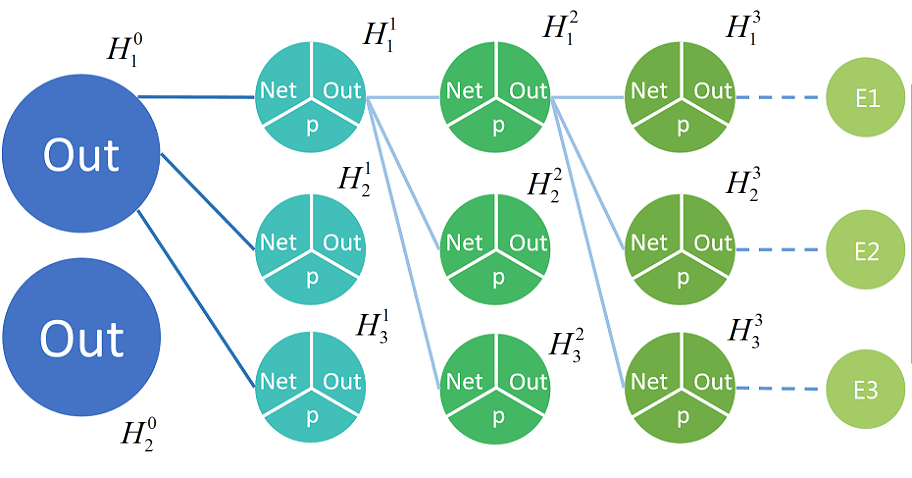
到了反向传播这一步,我们怎么做呢。。
第一步(注意我没有指明![]() 这样的神经元是用它的Out值还是Net,以图为准)
这样的神经元是用它的Out值还是Net,以图为准)
先求出第3层每一个神经元的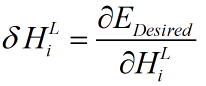 (公式中的
(公式中的![]() 只的是Net部分)
只的是Net部分)
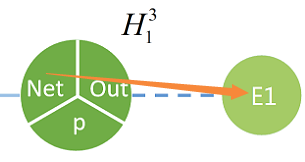 即这个net对咕价函数的“敏感度”
即这个net对咕价函数的“敏感度”
像这样,得到第三层每一个神经元的值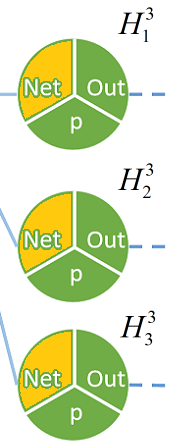 。橙色部分代表
。橙色部分代表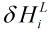
第二步
我们已经有足够的信息求出所有该层权值对估值的“敏感度” 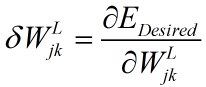 (
(![]() 即第L层第j个神经元到L-1层第k个神经元的边权)
即第L层第j个神经元到L-1层第k个神经元的边权)
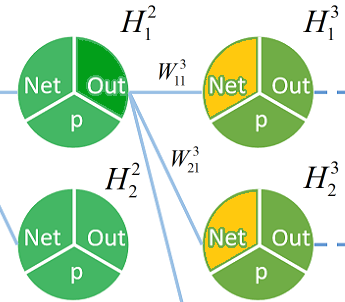
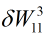 即为
即为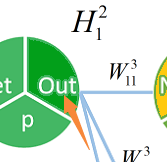 乘以
乘以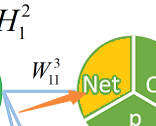 。。
。。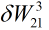 同理等于
同理等于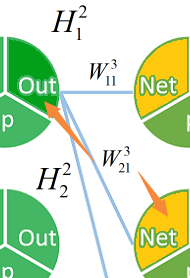 这个乘以这个。。
这个乘以这个。。
以此类推求出第三层所有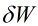
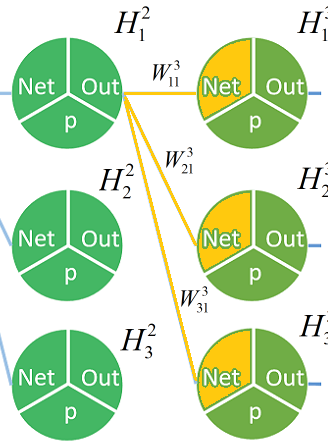
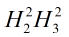 的
的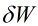 没画出来,橙色标记代表我们已经求出该值对估值的敏感程度
没画出来,橙色标记代表我们已经求出该值对估值的敏感程度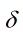
第三步
这一步需要推出前一层的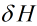
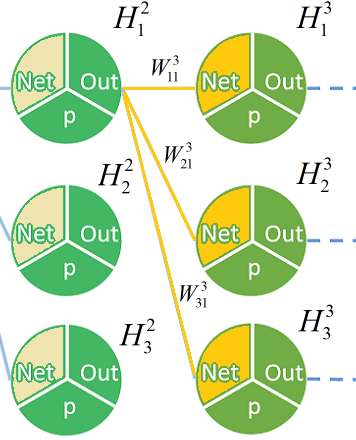 (粉色部分)
(粉色部分)
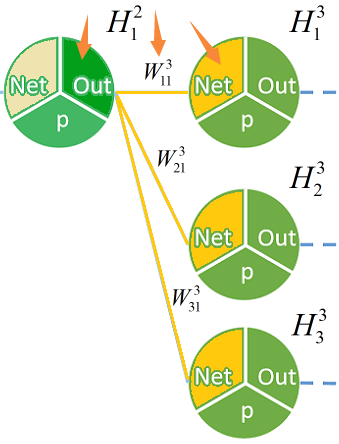 这个乘以这个乘以这个。(深绿色部分其实不是单纯相乘,而是要乘以
这个乘以这个乘以这个。(深绿色部分其实不是单纯相乘,而是要乘以 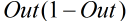 ,之后会有说明)
,之后会有说明)
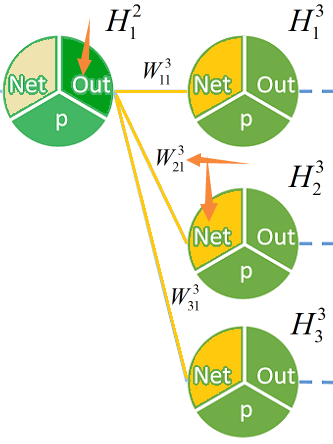 加上这个乘以这个乘以这个
加上这个乘以这个乘以这个
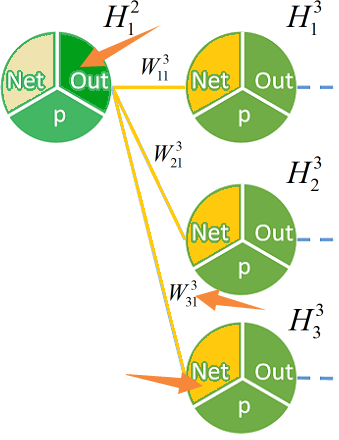 再加上这个乘以这个乘以这个
再加上这个乘以这个乘以这个
剩下两个神经元同理
第四步
重复以上三步,一直向前递推就好啦。一句话描述就是,先求出第N层的每个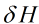 ,然后利用上一层的out部分求出每个
,然后利用上一层的out部分求出每个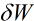 ,再利用本层的边权求出下一层的
,再利用本层的边权求出下一层的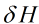 ,最后就是不断的向前重复递推。
,最后就是不断的向前重复递推。
相对直观的感受后(视频可能会更好,只是有心无力233)。。。
为什么可以这样呢 开始丢公式qwq
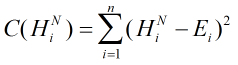 我们的估价函数长这样,则对任意一个
我们的估价函数长这样,则对任意一个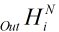 (最高层神经元的Out区域)求偏导
(最高层神经元的Out区域)求偏导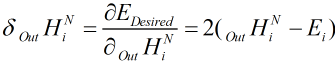
(包括后文,若出现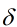 ,意思是
,意思是![]() )
)
然后我们想知道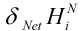 。。。
。。。
还记得激活函数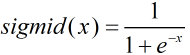 求导么,当x=
求导么,当x=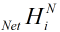 ,
,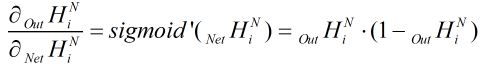
然后我们就可以求出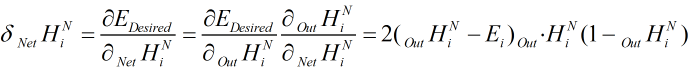
接着是求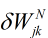 啦。我们看看涉及
啦。我们看看涉及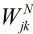 的公式,
的公式,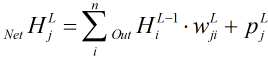 ,把
,把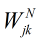 (
(![]() )看做自变量,求偏导得:
)看做自变量,求偏导得:
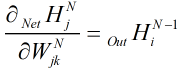
而,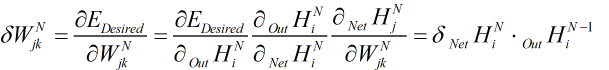
将N换成L,即对每一层它都成立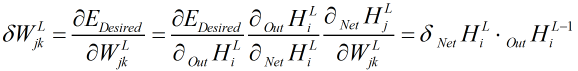
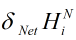 已求,
已求,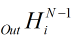 已知,那这不就很容易求出来了?
已知,那这不就很容易求出来了?
为了让前一层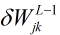 也容易求出来,我们有义务为前一层求出
也容易求出来,我们有义务为前一层求出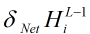 。再次利用公式
。再次利用公式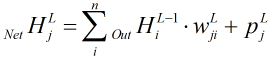 ,这次把
,这次把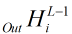 看做自变量,求偏导得
看做自变量,求偏导得
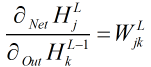
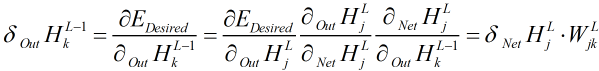 。注意,这里有个变量j,于是,我们还要遍历每一个j,结果累加
。注意,这里有个变量j,于是,我们还要遍历每一个j,结果累加
所以: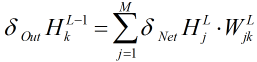
最后: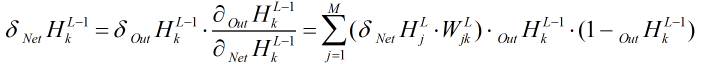
差不多就是这样啦,这里再稍微补充一个没有讲到关于偏置p的更新
还是这个公式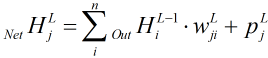 。这次我们让
。这次我们让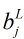 当自变量,那么一导,发现
当自变量,那么一导,发现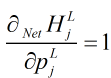
所以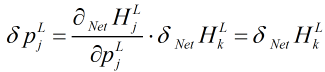
放上我的神经网络源码https://github.com/cckk4467/Nerve_Net
【参考资料】Charlotte77:https://www.cnblogs.com/charlotte77/p/5629865.html
3Blue1Brown:https://www.bilibili.com/video/av15532370、https://www.bilibili.com/video/av16144388、https://www.bilibili.com/video/av16577449


 浙公网安备 33010602011771号
浙公网安备 33010602011771号