AT_abc 复盘合集（2024）

AT_abc127 复盘

A

AC code:

#include <bits/stdc++.h>
#define int long long
#define memset(a, b) memset(a, b, sizeof(a))
#define pii pair<int, int>
#define fir first
#define sec second
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int a, b;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> a >> b;
	if (a >= 13) cout << b;
	else if (a >= 6) cout << b / 2;
	else cout << 0;
	return 0;
}

B

AC code:

#include <bits/stdc++.h>
#define int long long
#define memset(a, b) memset(a, b, sizeof(a))
#define pii pair<int, int>
#define fir first
#define sec second
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int r, d, x;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> r >> d >> x;
	for (int i = 1; i <= 10; i++) x = r * x - d, cout << x << endl;
	return 0;
}

C

很明显的线段树板子

AC code:

#include <bits/stdc++.h>
#define int long long
#define memset(a, b) memset(a, b, sizeof(a))
#define pii pair<int, int>
#define fir first
#define sec second
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int n, m;
struct node{
	int val, add;
}tr[N << 2];

void push_up(int p){
	tr[p].val = tr[p << 1].val + tr[p << 1 | 1].val;
}

void add(int p, int l, int r, int k){
	tr[p].val += (r - l + 1) * k;
	tr[p].add += k;
}

void push_down(int p, int l, int r){
	if (tr[p].add == 0) return ;
	int mid = l + r >> 1;
	add(p << 1, l, mid, tr[p].add);
	add(p << 1 | 1, mid + 1, r, tr[p].add);
	tr[p].add = 0;
}

void update(int p, int l, int r, int x, int y, int k){
	if (r < x || l > y) return ;
	if (x <= l && r <= y) return add(p, l, r, k), void();
	push_down(p, l, r);
	int mid = l + r >> 1;
	if (x <= mid) update(p << 1, l, mid, x, y, k);
	if (mid < y) update(p << 1 | 1, mid + 1, r, x, y, k);
	push_up(p);
}

int query(int p, int l, int r, int x, int y){
	if (r < x || l > y) return 0;
	if (x <= l && r <= y) return tr[p].val;
	push_down(p, l, r);
	int mid = l + r >> 1, res = 0;
	if (x <= mid) res += query(p << 1, l, mid, x, y);
	if (mid < y) res += query(p << 1 | 1, mid + 1, r, x, y);
	return res;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n >> m;
	for (int i = 1, l, r; i <= m; i++){
		cin >> l >> r;
		update(1, 1, n, l, r, 1);
	}
	int ans = 0;
	for (int i = 1; i <= n; i++){
		if (query(1, 1, n, i, i) == m) ans++;
	}
	cout << ans;
	return 0;
}

D

非常优雅的贪心。

考虑给 \(A\) 排序，\(B \ C\) 按 \(C\) 从大到小排，然后优先填大的进去，在手玩了几次发现没有反例，大概率是对的。

填数肯定是填比 \(C\) 小的，和 \(B\) 取个 \(\min\)。

AC code:

#include <bits/stdc++.h>
#define int long long
#define memset(a, b) memset(a, b, sizeof(a))
#define pii pair<int, int>
#define fir first
#define sec second
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int n, m, ans;
int a[N], s[N];
pii b[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= m; i++) cin >> b[i].sec >> b[i].fir;
	sort(a + 1, a + n + 1);
	sort(b + 1, b + m + 1, greater<pii>());
	for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
	int now = 1;
	for (int i = 1; i <= m; i++){
		int pos = lower_bound(a + 1, a + n + 1, b[i].fir) - a - 1;
		if (pos < now) continue;
		int len = min(b[i].sec, pos - now + 1);
		ans += len * b[i].fir - (s[now + len - 1] - s[now - 1]);
		now += len;
	} 
	cout << ans + s[n];
	return 0;
}

E

曼哈顿距离套路：分开算、暴力拆开。

此题暴力拆开非常难做，考虑分开算。

先取一对点出来看 \(x\) 坐标的贡献，不难发现它能贡献 \(C^{k-2}_{n\cdot m -2}\) 次，最终答案贡献 \(|x_i-x_j| \cdot C^{k-2}_{n\cdot m -2}\)，复杂度炸了。

我们看到会有很多 \(|x_i-x_j|\) 会重复，所以考虑枚举这个数 \(d\)。因为是点对（无序）所以直接假设 \(x_i < x_j\)，也就是 \(x_j=x_i+d\)，所以 \(x_i\) 的取值范围就是 \(1\le x_i\le n-d\) 在 \(y\) 方面没有限制，也就是有 \((n-d)\cdot m\) 种 \(x_i\)；而 \(x_j\) 限定了一种 \(y_j\) 同样没有限制，所以 \(d\) 能贡献 \((n-d) \cdot m^2\) 次，对答案造成 \((n-d) \cdot m^2 \cdot d \cdot C_{n \cdot m - 2}^{k-2}\) 的贡献。\(y\) 同理。

最终得到答案的式子：

\[\sum_{d=0}^{n-1}(n-d) \cdot m^2 \cdot d \cdot C_{n \cdot m - 2}^{k-2}+\sum_{d=0}^{m-1}(m-d) \cdot n^2 \cdot d \cdot C_{n \cdot m - 2}^{k-2} \]

当然，组合数那项可以提出来。

AC code:

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define fir first
#define sec second
#define endl '\n'
#define memset(a, b) memset(a, b, sizeof(a))
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int n, m, k, ans;
int fac[N], inv[N];

int ksm(int a, int b){
    int res = 1;
    while (b){
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int C(int a, int b){
    return fac[a] * inv[b] % mod * inv[a - b] % mod;
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n >> m >> k;
    fac[0] = inv[0] = 1;
    for (int i = 1; i <= N - 5; i++) fac[i] = fac[i - 1] * i % mod;
    inv[N - 5] = ksm(fac[N - 5], mod - 2);
    for (int i = N - 6; i >= 1; i--) inv[i] = (i + 1) * inv[i + 1] % mod;
    for (int i = 0; i <= n - 1; i++) ans = (ans + (n - i) * m % mod * m % mod * i % mod) % mod;
    for (int i = 0; i <= m - 1; i++) ans = (ans + (m - i) * n % mod * n % mod * i % mod) % mod;
    ans = ans * C(n * m - 2, k - 2) % mod;
    cout << ans;
    return 0;
}

F

初中数学，非常简单。

稍微学过初一上册的都知道绝对值的几何意义，转化完之后这题就是某练习册里面题目的 pro max，当 \(x\) 取到最中间就有最小值。

考虑维护最中间，我用了 vector 和 insert，复杂度 \(O(\text能过)\) 非常快速。找到了最小值对应的 \(x\) 接下来就是找 \(f(x)\)。在多玩几组数据之后轻松发现加上一个点的贡献就是最中间点到他的距离，这题就结束了。

注：细节巨多，特别是判断奇偶的部分，多造几组数据跑跑。

AC code:

#include <bits/stdc++.h>
#define int long long
#define memset(a, b) memset(a, b, sizeof(a))
#define pii pair<int, int>
#define fir first
#define sec second
using namespace std;

const int N = 2e5 + 5;
const int mod = 1e9 + 7;

int q;
vector<int> v;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr); cout.tie(nullptr);
	cin >> q;
	int val = 0;
	for (int i = 1, op, a, b; i <= q; i++){
		cin >> op;
		if (op == 1){
			cin >> a >> b;
			if (v.size() & 1) val += abs(v[v.size() / 2] - a);
			v.insert(upper_bound(v.begin(), v.end(), a), a);
			if (v.size() & 1) val += abs(v[v.size() / 2] - a);
			val += b;
		}
		else{
			if (v.size() % 2 == 0) cout << v[v.size() / 2 - 1] << " " << val << endl;
			else cout << v[v.size() / 2] << " " << val << endl;
		}
	}
	return 0;
}

AT_abc131 复盘

A

for + if

AC code:

#include <bits/stdc++.h>
using namespace std;

string s;

int main(){
    cin >> s;
    for (int i = 1; i < s.size(); i++){
        if (s[i] == s[i - 1]) return cout << "Bad", 0;
    }
    cout << "Good";
    return 0;
}

B

阅读理解，之间枚举哪一个不选

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, l, ans = 1e18, tmp, cnt;
int a[200005];

signed main(){
    cin >> n >> l; 
    for (int i = 1; i <= n; i++) a[i] = l + i - 1;
    for (int i = 1; i <= n; i++) tmp += a[i];
    for (int i = 1; i <= n; i++){
        int sum = 0;
        for (int j = 1; j <= n; j++){
            if (i == j) continue;
            sum += a[j];
        }
        if (abs(tmp - sum) < ans) ans = abs(tmp - sum), cnt = sum;
    }
    cout << cnt;
    return 0;
}

C

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int a, b, c, d;

signed main(){
    cin >> a >> b >> c >> d;
    cout << (b - a + 1) - (((b / c + b / d - b / (c * d / __gcd(c, d)))) - ((a - 1) / c + (a - 1) / d - (a - 1) / (c * d / __gcd(c, d))));
    return 0;
}

D

直接按 \(b\) 排序，然后模拟一遍，正确性显然

AC code:

#include <bits/stdc++.h>
#define Luke return
#define Forever 0
#define int long long
using namespace std;

int n;
struct node{
	int x, y;
	bool operator < (const node& rhs) const {
		if (y == rhs.y) return x < rhs.x;
		return y < rhs.y;
	}
}a[200005];

signed main(int argc, char **argv){
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i].x >> a[i].y;
	sort(a + 1, a + n + 1);
	int tim = 0, lmt = 0;
	for (int i = 1; i <= n; i++){
		tim += a[i].x, lmt = a[i].y;
		if (tim > lmt) return cout << "No", 0;
	}
	cout << "Yes";
	Luke Forever;
}

E

很容易想到菊花图，这种情况下叶子节点两两之间都满足要求，总共有 \((n-1)\times(n-2)\) 对，也是最多的情况。

我们考虑加边，算一下加边的贡献。模拟一遍，不难发现加一条边在两个叶子节点中间的贡献就是 \(-1\)，也就是把这两个叶子节点间的贡献去掉。只要加 \((n-1)\times(n-2)-k\) 条边就能满足条件。

实现方面，先构建一个菊花图，然后加边。对于加边的判重只需要先预处理出可以加的边（\(n^2\) 一遍塞到队列里），如果欧气足够直接 random 后判重也行。

AC code:

#include <bits/stdc++.h>
#define Luke return
#define Forever 0
#define int long long
using namespace std;

int n, k, cnt;
vector<int> g[105];
queue<pair<int, int>> q;

signed main(int argc, char **argv){
    cin >> n >> k;
    if (k > (n - 1) * (n - 2) / 2) return cout << -1, 0;//判断是否超过最大值
    for (int i = 2; i <= n; i++){
        for (int j = i + 1; j <= n; j++) q.push({i, j});//预处理
    }
    for (int i = 2; i <= n; i++) g[1].push_back(i), cnt++;//构建菊花图
    int now = (n - 1) * (n - 2) / 2;
    while (now > k){//不断在叶子节点间加边
        int x = q.front().first, y = q.front().second; q.pop();
        g[x].push_back(y);
        cnt++, now--;
    }
    cout << cnt << endl;
    for (int i = 1; i <= n; i++){
        for (int j = 0; j < g[i].size(); j++) cout << i << " " << g[i][j] << endl;
    }
    Luke Forever;
}

F

直接计算每个点的贡献肯定不好算，转换一下手玩一下，发现一个点相当于把行和列连接起来了，而最终贡献就是这个行点的个数乘以这个列的个数？

好像并不是，再玩一下，可能是通过一个“连通块”中所有行的个数乘以所有列的个数；不难想到可以用并查集，每次加点就把行和列合并了，最终统计一下每个连通块的贡献相加就好。

但答案好像不对？再看一遍样例，发现所有给出的点会被算到答案中，那么减去它们就好了。

AC code：

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, ans;
int x[100005], y[100005], fa[200005], r[200005], c[200005];

int find(int x){
	return (x == fa[x] ? x : fa[x] = find(fa[x]));
}

signed main(int argc, char **argv){
	cin >> n;
	for (int i = 1; i <= 2e5; i++) fa[i] = i;
	for (int i = 1; i <= n; i++){
		cin >> x[i] >> y[i];
		fa[find(x[i])] = find(y[i] + 1e5);
	}
	for (int i = 1; i <= 1e5; i++) r[find(i)]++;//统计连通块中行的个数
	for (int i = 1e5 + 1; i <= 2e5; i++) c[find(i)]++;//列的个数
	for (int i = 1; i <= 2e5; i++) ans += r[i] * c[i];//答案就是行的个数乘以列的个数
	cout << ans - n;//答案要减去原来的点
	return 0;
}

AT_abc147 复盘

A

B

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

string s;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> s;
	int cnt = 0;
	for (int i = 0; i < s.size() / 2; i++){
		if (s[i] != s[s.size() - i - 1]) cnt++;
	}
	cout << cnt;
	return 0;
}

C

有点若只，只需要状压一下然后只考虑 \(1\) 的位置连出去的边有没有矛盾的。

AC code:

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define fir first
#define sec second
#define memset(a, b) memset(a, b, sizeof(a))
using namespace std;

const int N = 15 + 5;

int n, ans;
int a[N], vis[N];
vector<pii> v[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++){
		cin >> a[i];
		for (int j = 1, x, y; j <= a[i]; j++){
			cin >> x >> y;
			v[i].push_back({x, y});
		}
	}
	for (int i = 0; i < (1 << n); i++){
		memset(vis, 0);
		for (int j = 1; j <= n; j++) vis[j] = ((i >> (j - 1)) & 1);
		int flag = 0, cnt = 0;
		for (int j = 1; j <= n; j++){
			if (vis[j] == 1){
				cnt++;
				for (int k = 0; k < a[j]; k++){
					int x = v[j][k].fir, y = v[j][k].sec;
					if (vis[x] != y) flag = 1;
				}
			}
		}
		if (!flag) ans = max(ans, cnt);
	}
	cout << ans;
	return 0;
}

D

非常简单，拆位，考虑每一位的贡献。从后往前遍历，分别记录 \(1\) 和 \(0\) 的个数，与当前相反的就能造成贡献。

取模是什么啊？——队爷

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 3e5 + 5;
const int mod = 1e9 + 7;

int n, ans;
int a[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int j = 0; j <= 60; j++){
		int cnt0 = 0, cnt1 = 0;
		for (int i = n; i >= 1; i--){
			if ((a[i] >> j) & 1ll) ans = (ans + (1ll << j) % mod * cnt0 % mod) % mod, cnt1++;
			else ans = (ans + (1ll << j) % mod * cnt1 % mod) % mod, cnt0++;
		}
	}
	cout << ans;
	return 0;
}

E

一眼过去没思路，直接跳了。。。

其实非常简单，看到两个值不好操作，把两个压成一个也就是变成差值的绝对值；标记操作就变成了到这个格子减去或加上这里的值。

这样就可以简单 \(dp\) 了，设 \(dp_{i,j,k}\) 表示为在第 \(i\) 行 \(j\) 列能不能取到 \(k\)，转移就从 两个方向+加上或减去 转移。

有个细节，因为有负数，所以要加上一个数。

空间要开够！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！

AC code:

// LUOGU_RID: 174983639
#include <bits/stdc++.h>
using namespace std;

const int N = 85;

int h, w;
int a[N][N], b[N][N], c[N][N];
bool dp[N][N][4 * N * N + 5];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> h >> w;
	for (int i = 1; i <= h; i++){
		for (int j = 1; j <= w; j++) cin >> a[i][j];
	}
	for (int i = 1; i <= h; i++){
		for (int j = 1; j <= w; j++) cin >> b[i][j];
	}
	for (int i = 1; i <= h; i++){
		for (int j = 1; j <= w; j++) c[i][j] = abs(a[i][j] - b[i][j]);
	}
	dp[1][1][c[1][1] + 2 * N * N] = 1;
	dp[1][1][c[1][1]] = 1;
	for (int i = 1; i <= h; i++){
		for (int j = 1; j <= w; j++){
		  if(i == 1 && j == 1) continue;
			for (int k = 0; k <= 4 * N * N; k++){
				if (k - c[i][j] >= 0){
					dp[i][j][k] |= dp[i - 1][j][k - c[i][j]];
					dp[i][j][k] |= dp[i][j - 1][k - c[i][j]];
				}
				if (k + c[i][j] <= 4 * N * N){
					dp[i][j][k] |= dp[i - 1][j][k + c[i][j]];
					dp[i][j][k] |= dp[i][j - 1][k + c[i][j]];
				}
			}
		}
	}
	int ans = 1e9;
	for (int k = 0; k <= 4 * N * N; k++){
		if (dp[h][w][k] == 1) ans = min(ans, abs(2 * N * N - k));
	}
	cout << ans;
	return 0;
}

F

考虑转换一下式子：

\[w(S)=\sum_{i\in S}A_i-\sum_{i\not\in S}A_i \\ \]

因为有：

\[\sum_{i\in S}A_i + \sum_{i\not\in S}A_i=\sum_{i=1}^{N} A_i \]

不难得出：

\[w(S)=2\times \sum_{i\in S}A_i-\sum_{i=1}^{N} A_i \]

第一步转换完成了，后面 \(\sum_{i=1}^NA_i\) 是定值，所以总可能性就变成了前面一部分的种数。

再考虑每个数的表示方式：

\[A_i=X+(i-1)\cdot D \]

所以等差数列中 \(p\) 项的和可以表示为，其中 \(k\) 是所选数下标减 \(1\) 的和：

\[s=p\cdot X + k \cdot D \]

稍微手玩一下可以发现一个性质，在 \(p\) 不变的情况下，\(k\) 的取值范围是一个连续的区间。具体的，\(k\in[\frac{(i-1)\cdot i}{2},\frac{(2\cdot n-i-1)\cdot i}{2}]\)。

很明显这样算会有重复，考虑什么情况会有重复发生，不难想到，如果满足如下式子就有可能会有重复：

\[p_i \cdot X+k_i\cdot D =p_j\cdot X+k_j\cdot D\\ p_i\cdot X \equiv p_j \cdot X (\bmod D) \]

形象的，每一个和都是由 \(X\) 的倍数加上 \(D\) 的倍数构成的，而对于 \(p\) 相同 \(k\) 不同的和也是一个等差数列，所以这个等差数列的“首项”和另外一个的模 \(D\) 同余的话那就有可能重复。如果已经满足上述条件了，那就可以到下一步判断两个等差数列是否有交集了，可以当作线段之间有没有重合部分去做（因为公差一样又同余所以可以比较边界判断有没有重合）。

为了方便，我们可以采取类似离线的方式，把每一条线段记录下来，按左端点排序（左端点指的是 \(p\) 固定下 \(k\) 取最小的 \(s\)，右端点同理），新产生的贡献肯定是在之前线段的最右端点往右的部分才有贡献，所以只用记录端点最靠右的一段连续区间，每次比较一下记录贡献和维护这个区间。

对于贡献的记录就是类似等差数列的方法，用求项数的方法求就好，注意有时候要处理边界。

一切看似都如此顺利，但是当 \(p<0\) 时好像就挂了，没关系，对于样例二输出一下运行时的参数，发现有些线段的左端点和右端点反了（事实上是全部），那么在记录线段的时候特判一下反转掉就行。但是还是挂了，我们发现算贡献等差数列求项数除了一个负的公差，很简单，加个绝对值就行。简简单单就过了。

反转其实是为了保证上面可以简单维护区间。

AC code:

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define fir first
#define sec second
#define endl '\n'
#define memset(a, b) memset(a, b, sizeof(a))
using namespace std;

const int N = 2e5 + 5, M = 10 + 5;
const int mod = 998244353;

int n, x, d, ans;
map<int, vector<pii>> mp;

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n >> x >> d;
    if (d == 0 && x == 0) return cout << 1, 0;
    if (d == 0) return cout << n + 1, 0;                                        
    for (int i = 0; i <= n; i++){
        int tmp = i * x % d;
        int st = (i - 1) * i / 2, ed = (n - i + n - 1) * i / 2;
        if (d < 0) swap(st, ed);//小小操作一下，让左端点比右端点小
        mp[tmp].push_back({st * d + i * x, ed * d + i * x});//记录每一条线段
    }
    for (auto it : mp){
        sort(it.sec.begin(), it.sec.end());//按左端点排序
        int l = it.sec[0].fir, r = it.sec[0].sec;
        ans += (r - l) / abs(d) + 1;//初始先放进来一条线段
        for (int j = 1; j < it.sec.size(); j++){
            int tl = it.sec[j].fir, tr = it.sec[j].sec;//不断取出来一条线段取维护这个“最右线段”
            if (tl <= r) ans += max(tr - r, 0ll) / abs(d), r = max(r, tr);//有重合，算上最右端点往右的贡献
            else ans += (tr - tl) / abs(d) + 1, l = tl, r = tr;//没重合，直接加上这一段的贡献
            //                      因为上面保证了左端点比右端点小，所以公差也必须是正的
        }
    }
    cout << ans;
    return 0;
}

AT_abc179 复盘

好久没写复盘了。。。。

A

非常有意思的一道题，使我英语白学

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 2e5 + 5;
const int mod = 998244353;

string s;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> s;
	if (s[s.size() - 1] == 's') cout << s << "es";
	else cout << s << "s";
	return 0;
}

B

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 2e5 + 5;
const int mod = 998244353;

int n;
int a[N], b[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
	for (int i = 3; i <= n; i++){
		if (a[i - 2] == b[i - 2] && a[i - 1] == b[i - 1] && a[i] == b[i]) return cout << "Yes", 0;
	}
	cout << "No";
	return 0;
}

C

还行，一眼枚举 \(A\) 特判一下整除 \(C=0\) 的情况

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1e6 + 5;
const int mod = 998244353;

int n, ans;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++){
		ans += n / i;
		if (n % i == 0) ans--;
	}
	cout << ans;
	return 0;
}

D

此题难度严重大于 EF。

祭文提供了一种神秘的做法。普通思路我想可以直接参考题解。

考虑每一个 \(dp_i\) 的转移区间，发现 \(dp_{i+1}\) 的转移区间相当于 \(dp_i\) 向右平移了一格，就可以直接滑动窗口那样删去平移掉的，加上新进来的，就结束了。

注意：我们维护的是转移区间里的和，不代表 \(dp_{i+1}\) 修改前的转移区间和可以表示成 \(dp_i\)。

普通做法是发现转移区间是 \(k\) 个连续的区间直接前缀和优化掉，比较直观且简单。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 2e5 + 5;
const int mod = 998244353;

int n, k;
int l[N], r[N], dp[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n >> k;
	for (int i = 1; i <= k; i++){
		cin >> l[i] >> r[i];
	} 
	dp[1] = 1;
	int tmp = 0;
	for (int i = 2; i <= n; i++){
		for (int j = 1; j <= k; j++){
			if (i - l[j] >= 1) tmp = (tmp + dp[i - l[j]]) % mod;
			if (i - r[j] - 1 >= 1) tmp = (tmp - dp[i - r[j] - 1]) % mod;
		}
		dp[i] = (tmp % mod + mod) % mod;
	}
	cout << dp[n];
	return 0;
}

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define fir first
#define sec second
#define endl '\n'
#define memset(a, b) memset(a, b, sizeof(a))
using namespace std;

const int N = 2e5 + 5, M = 10 + 5;
const int mod = 998244353;

int n, m, ans;
int l[N], r[N], dp[N], s[N];

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) cin >> l[i] >> r[i];
    dp[1] = s[1] = 1;
    for (int i = 2; i <= n; i++){
        for (int j = 1; j <= m; j++){
            dp[i] += s[max(0ll, i - l[j])] - s[max(0ll, i - r[j] - 1)];
            dp[i] = (dp[i] + mod) % mod;
        }
        s[i] = (s[i - 1] + dp[i]) % mod;
    }
    cout << dp[n];
    return 0;
}

E

发现模数不是很大，而项数很大，不难想到可以直接找循环节（这个方法还是很有用的）。拿个 \(vis\) 数组记录 \(a_i\) 第一次出现的位置，如果重复出现说明循环节找到了，可以直接把数列分为三部分：前面不循环的、循环的、多余的。每一个部分都可以在 \(O(\text 能过)\) 的复杂度下解决，稍微推点式子统计一下即可。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 2e5 + 5;

int n, x, mod, ans;
int a[N], vis[N], s[N];

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n >> x >> mod;
	a[1] = x, s[1] = x;
	vis[a[1]] = 1;
	for (int i = 2; i <= n; i++){
		a[i] = a[i - 1] * a[i - 1] % mod;
		s[i] = s[i - 1] + a[i];
		if (vis[a[i]]){
			int len = i - vis[a[i]], val = s[i - 1] - s[vis[a[i]] - 1];
			int tmp = (n - vis[a[i]] + 1) / len * val;
			tmp += s[vis[a[i]] + (n - i + 1) % len - 1] - s[vis[a[i]] - 1];
			return cout << s[vis[a[i]] - 1] + tmp, 0;
		} 
		vis[a[i]] = i;
		if (a[i] == 1) return cout << s[i] + (n - i), 0;
		if (a[i] == 0) return cout << s[i], 0;
	}
	cout << s[n];
	return 0;
}

F

口胡出来了。。。。

考虑模拟，我们发现每一次操作列所更改的是这一列上行号最小的白子到最上方的格子；每一次操作列带来的贡献是所更改的对应行上操作的值，值代表着这一行上出现的列号最小的白子。到这里不难看出要使用神秘的数据结构，考虑维护信息。操作行就是更改对应列的行号最小的白子，也就是区间修改最小值；查询对应行列号最小的白子，就是单点查询最小值。对于答案的贡献也非常明了，直接拿最小的对应位置减去 \(2\) 就是删去黑子的贡献（这里保证了操作不重复所以能偷懒）。

注意：树状数组把修改下标反一下就能实现更改前缀。

两个树状数组可能会让你调到怀疑人生。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 2e5 + 5;
const int mod = 998244353;

int n, q;

struct node{
	int c[N];
	
	void update(int x, int k){
		x = n - x + 1;
		for (; x <= n; x += x & (-x)) c[x] = min(c[x], k);
	}
	
	int query(int x){
		int res = 0x3f3f3f3f3f3f3f3f;
		x = n - x + 1;
		for (; x; x -= x & (-x)) res = min(res, c[x]);
		return res;
	}
}tr1, tr2;//struct 的正确用法

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> n >> q;
	int ans = (n - 2) * (n - 2);
	memset(tr1.c, 0x3f, sizeof(tr1.c));
	memset(tr2.c, 0x3f, sizeof(tr2.c));
	tr1.update(n, n); tr2.update(n, n);
	for (int i = 1, op, x; i <= q; i++){
		cin >> op >> x;
		if (op == 1){
			int tmp = tr1.query(x);
			ans -= (tmp - 2);
			tr2.update(tmp, x);
		}
		else{
			int tmp = tr2.query(x);
			ans -= (tmp - 2);
			tr1.update(tmp, x);
		}
	}
	cout << ans;
	return 0;
}

AT_abc191 复盘

A

if

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int a, b, c, d;

signed main(){
	cin >> a >> b >> c >> d;
	if ((a * b <= d && d <= a * c) || (a * c <= d && d <= a * b)) cout << "No";
	else cout << "Yes";
	return 0;
}

B

特判

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, x, a;

signed main(){
	cin >> n >> x;
	for (int i = 1; i <= n; i++){
		cin >> a;
		if (a == x) continue;
		cout << a << " ";
	}
	return 0;
}

C

横着扫一遍，竖着扫一遍，如果当前点是一条边就加一，注意判断左边和右边的区别。

对于判断是否统计过答案，只要判断上一个点的情况是否和当前点的情况一样就刑。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, m, ans;
string s[15];

signed main(){
	cin >> n >> m;
	for (int i = 0; i < n; i++) cin >> s[i];
	for (int i = 1; i < n - 1; i++){
		int cnt = 0;
		for (int j = 1; j < m; j++){
			if (s[i][j] == '#' && s[i][j - 1] == '.' && !(s[i - 1][j] == '#' && s[i - 1][j - 1] == '.')) cnt++;
			if (s[i][j] == '.' && s[i][j - 1] == '#' && !(s[i - 1][j] == '.' && s[i - 1][j - 1] == '#')) cnt++;
		}
		ans += cnt;
	}
	for (int j = 1; j < m - 1; j++){
		int cnt = 0;
		for (int i = 1; i < n; i++){
			if (s[i][j] == '#' && s[i - 1][j] == '.' && !(s[i][j - 1] == '#' && s[i - 1][j - 1] == '.')) cnt++;
			if (s[i][j] == '.' && s[i - 1][j] == '#' && !(s[i][j - 1] == '.' && s[i - 1][j - 1] == '#')) cnt++;
		}
		ans += cnt;
	}
	cout << ans;
	return 0;
}

D

直接上圆的方程 \(x^2+y^2=r^2\)，这里设远点为 \(x_0,y_0\)，那么方程变为 \((x-x_0)^2+(y-y_0)^2=r^2\)。

我们可以考虑只遍历所有满足条件的 \(x\) 然后求出满足条件 \(y\) 的个数。稍微变形一下公式 \(y=\sqrt{r^2-(x-x_0)^2}+y_0\)，这里求的是较上面的那个在圆上的 \(y\) 值，那么在下面的就是 \(y'=2y_0-y\)（圆的对称性）。统计答案类似前缀和，等于 \(\lfloor y \rfloor-\lfloor y' \rfloor\)，这里要特判一下 \(y'\) 是否为整数，如果是还要加 \(1\)。

注意：这题卡精度，可以给 \(r\) 加上一个极小值解决（开根号可能会把小数点后几位抹除）。

AC code:

#include <bits/stdc++.h>
#define int long long
#define double long double
using namespace std;

int ans;
double x, y, r;

signed main(){
	cin >> x >> y >> r;
	r += 1e-14;//卡精度
	for (int i = ceil(x - r); i <= floor(x + r); i++){
		double tmp = sqrt(r * r - (i * 1.0 - x) * (i * 1.0 - x)) + y;//y
		double tmp1 = y + y - tmp;//y'
		if (floor(tmp1) == tmp1) ans++;//特判y'是否为整数
		ans += floor(tmp) - floor(tmp1);//统计答案
	}
	cout << ans;
	return 0;
}

E

Dijkstra 板子。

按照 dij 的思路，我们能在 \(mlogn\) 的复杂度内处理一个点到所有其他点的距离，但自己的求不到。

为什么求不到？因为 \(dis_x\) 已经被标记为 \(0\) 了，不可能有更短路径，但只需要先把 \(x\) 的子节点入队，更新 \(dis\)，但保留 \(dis_x=\inf\)，这样就能做到求出从自己出发到自己的环的最小距离。

注意：这题有重边和自环，加边的时候去边权最小的边，自环要在 dij 之后特判一下。

AC code:

#include <bits/stdc++.h>
#define pii pair<int, int>
#define int long long
using namespace std;

int n, m;
int dis[2005], t[2005];
vector<pii> g[2005];
map<pair<int, int>, int> mp;

void dij(int x){
	priority_queue<pii, vector<pii>, greater<pii>> q;
	memset(dis, 0x3f, sizeof(dis));
	for (int i = 0; i < g[x].size(); i++) dis[g[x][i].first] = g[x][i].second, q.push({dis[g[x][i].first], g[x][i].first});
	while (!q.empty()){
		int u = q.top().second; q.pop();
		for (int i = 0; i < g[u].size(); i++){
			int v = g[u][i].first, w = g[u][i].second;
			if (dis[v] > dis[u] + w){
				dis[v] = dis[u] + w;
				q.push({dis[v], v});
			}
		}
	}
}

signed main(){
	cin >> n >> m;
	memset(t, -1, sizeof(t));
	for (int i = 1, u, v, w; i <= m; i++){
		cin >> u >> v >> w;
		if (u == v) t[u] = w;
		if (mp[{u, v}]) mp[{u, v}] = min(mp[{u, v}], w);
		else mp[{u, v}] = w;
	}
	for (auto it : mp) g[it.first.first].push_back({it.first.second, it.second});
	for (int i = 1; i <= n; i++){
		dij(i);
		if (t[i] != -1 && t[i] < dis[i]) cout << t[i] << endl;
		else{
			if (dis[i] == 0x3f3f3f3f3f3f3f3f) cout << "-1\n";
			else cout << dis[i] << endl;
		}
	}
	return 0;
}

F

首先考虑弱化版：只有 \(\gcd\) 或者只有 \(\min\)。显然是所有数的 \(\gcd\) 或者所有数的 \(\min\)。

而 \(\min\) 有一个性质：做一次操作，相当于删掉比它大的数。那我们就可以对任意一个 \(\gcd\) 状态进行一遍这个操作，只要这个值是最小的，我们就能取到这个值。那这个答案可以转化成：取任意次 \(\gcd\)，再取 \(\min\)，满足要求的种数有多少。但有一个显然的约束，当 \(\gcd\) 后的数为 \(x\)，但 \(x > \min \{a_i\}\)，最后取 \(\min\) 之后肯定不会是 \(\gcd\) 这个值。

现在我们只需要记录有多少种 \(\gcd\) 的值小于等于 \(\min\{a_i\}\)，然后累加答案就行了 ……吗？还要加一个特判，这些取的数的 \(\gcd\) 是否真的是这个值，只需要维护一个 map 取存当前质因数所对应的倍数的 \(\gcd\)。而我们可以直接遍历一遍所有数，对于每一个数所含的因子与 \(mp_j\) 去做一遍 \(\gcd\) 判断是否满足条件。

正确性：如果当前因数为 \(x\)，那么所并进来的数一定是 \(x\) 的倍数，而 \(\gcd\) 的值肯定是大于等于 \(x\) 的。考虑不满足条件的时候——这堆数的 \(\gcd\) 不是 \(x\)，也就是有更大的数，肯定在一遍 \(\gcd\) 后能找出来。换句话说，\(mp_j\) 的值肯定是 \(\ge j\) 的，取一个数后 \(mp_j\) 不可能会减小，所以能够判断。

AC code：

#include <bits/stdc++.h>
using namespace std;

int n, ans;
int a[2005];
map<int, int> mp;

int main(){
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	sort(a + 1, a + n + 1);
	for (int i = 1; i <= n; i++){
		for (int j = 1; j <= sqrt(a[i]); j++){
			if (a[i] % j == 0){
				if (j <= a[1]) mp[j] = __gcd(mp[j], a[i]);
				if (a[i] / j <= a[1]) mp[a[i] / j] = __gcd(mp[a[i] / j], a[i]);
			}
		}
	}
	for (auto it : mp) ans += (it.first == it.second);
	cout << ans;
	return 0;
}

AT_abc208 复盘

A

AC code:

#include <bits/stdc++.h>
using namespace std;

int a, b;

int main(){
	cin >> a >> b;
	if (a > b || a * 6 < b) cout << "No";
	else cout << "Yes";
	return 0;
}

B

随便拿个 map 搞搞

AC code:

#include <bits/stdc++.h>
using namespace std;

string a;
map<string, int> mp;

int main(){
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	if (mp.size() != 4) cout << "No";
	else cout << "Yes";
	return 0;
}

C

sort

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, k, sum;
int ans[200005];
pair<int, int> a[200005];

signed main(){
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i].first, a[i].second = i;
	sum += k / n, k %= n;
	sort(a + 1, a + n + 1);
	for (int i = 1; i <= k; i++) ans[a[i].second]++;
	for (int i = 1; i <= n; i++) cout << sum + ans[i] << endl;
	return 0;
}

D

Floyd，跟普通的 Floyd 一样，只不过多记录一维。

设 \(dp_{i,j,k}\) 表示从 \(i\) 到 \(j\) 最大值不超过 \(k\) 的最短路长度，转移很显然，设中间点为 \(p\)，那么 \(dp_{i,j,p} = \min(dp_{i,j,p-1},dp_{i,p,p-1}+dp_{p,j,p-1})\)。

对于枚举每一个中间点，都要统计一边答案，如果 \(dp_{i,j,p}\le \inf\) 那么统计一次答案。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, m, ans;
int dp[405][405][405];

signed main(){
	cin >> n >> m;
	memset(dp, 0x3f, sizeof(dp));
	for (int i = 1, u, v, w; i <= m; i++){
		cin >> u >> v >> w;
		dp[u][v][0] = w;
	}
	for (int i = 1; i <= n; i++){
		for (int j = 0; j <= n; j++) dp[i][i][j] = 0;
	}
	for (int k = 1; k <= n; k++){
		for (int i = 1; i <= n; i++){
			for (int j = 1; j <= n; j++){
				dp[i][j][k] = min(dp[i][j][k - 1], dp[i][k][k - 1] + dp[k][j][k - 1]);
			}
		}
		for (int i = 1; i <= n; i++){
			for (int j = 1; j <= n; j++){
				if (dp[i][j][k] < 1e16) ans += dp[i][j][k];
			}
		}
	}
	cout << ans;
	return 0;
}

E

首先肯定想到数位 dp，但要处理的信息太多，不方便设计 dp，所以考虑记忆化搜索。

从最基本的开始，设 \(dfs(x,mul)\) 表示填到第 \(x\) 位乘积不大于 \(mul\) 的方案数。转移很简单，考虑这一位选什么，然后去 \(dfs\) 下一位。这里转移的时候其实不朽要考虑乘积是否小于等于 \(k\)，只需要最后判断一下整个数的乘积是否小于。

那限制条件呢？先来看 \(\le n\) 的条件。\(dfs\) 的时候多加一个参数，判断这一位是否有 \(\le n\) 的限制，如果有，那么填的数最大只能到 \(a_x\)；这个条件很显然是加在转移的时候，如果这一位有限制，并且已经取到限制了，那么下一位也有限制。具体的，如果 \(limit=1\) 并且 \(i=maxx\)，那么就要传递标记。

没了吗？不，还有前导 \(0\)。一个数真正对答案的贡献其实是除去前导 \(0\) 剩下的数的乘积，那么还需要维护一个 \(lead\) 判断这上一位是不是前导 \(0\)；对于 \(lead\) 的维护，很显然如果 \(lead\) 本身为 \(1\)，并且所填的数 \(i=0\)，那么就传递下去。转移的时候 \(mul\) 的值也不能算前导 \(0\) 的贡献，有了 \(lead\) 之后直接特判几下：

• 上一位属于前导 \(0\)，这一位也属于，\(mul\) 不变。
• 上一位属于前导 \(0\)，这一位不属于，\(mul\) 赋值成 \(i\)。
• 本来就不是前导 \(0\)，直接更新 \(mul\) 成 \(mul \times i\)。

接下来就是记忆化部分，设 \(dp\) 每一维对应着 \(dfs\)，记录着这种情况的方案数。在转移前，判断一下是否遍历过，如果有，直接 return。而 \(mul\) 有可能很大，但是可能的乘积不多，所以把这一位放进 map 维护。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, k, len;
int a[20];
map<int, int> dp[20][2][2];

int dfs(int x, bool limit, bool lead, int mul){
	if (!x) return mul <= k;//如果填完了，并且乘积满足条件，答案加1
	if (dp[x][limit][lead].count(mul)) return dp[x][limit][lead][mul];//是否出现过，不能用 == 0，有可能这个函数值本身就是0
	int res = 0, maxx = limit ? a[x] : 9;//判断是否有限制
	for (int i = 0; i <= maxx; i++){
		int tmp = 0;
		if (lead && i == 0) tmp = mul;//前导0部分
		else if (lead && i != 0) tmp = i;
		else tmp = mul * i;
		res += dfs(x - 1, limit && (i == maxx), lead && (i == 0), tmp);//各种条件的转移
	}
	return dp[x][limit][lead][mul] = res;//记忆化
}

signed main(){
	cin >> n >> k;
	while (n) a[++len] = n % 10, n /= 10;
	cout << dfs(len, 1, 1, 0) - 1;//把0减去
	return 0;
}

F

前置知识：拉格朗日插值 或 OI-wiki；多项式请参考七年级上册数学书。

观察式子，最终所有式子肯定都是到第二种情况，也就是 \(i^k\) 其中 \(1\le i\le n\)，问题就变成了每一个 \(i^k\) 对答案的贡献是多少，然后累加一下。

假设 \(a_{i,j}\) 为 \(n=i,m=j\) 时的总方案数，稍微打一下表，发现 \(a_{i,j}=a_{i-1,j}+a_{i,j-1}\)，这很类似于“只能往下或左走，请问有多少种方案”的问题，不难得出在方案数有 \(C_{n-i+m-1}^{m-1}\) 其中开始位置为 \((i,0)\)，终点为 \((n,m)\)，也就是 \(i^k\) 对答案的贡献。故最后答案为：

\[\sum_{i=0}^{n}i^k\times C_{n-i+m-1}^{m-1} \]

上面的办法肯定是会爆的，考虑拉格朗日插值，我们需要求 \(f(n)\) 也就是只用找到多项式次数 \(l\) 再加上 \(0\) 次，也就是 \(l+1\) 个观测点的值套一遍公式就能求出来。那次数 \(l\) 是多少呢？考虑把上面的多项式拆开来看（把组合数拆开），变成：

\[\sum_{i=0}^{n}i^k \times \frac{(n-i+m-1)!}{(m-1)!(n-i)!} \]

这里我们要求的是关于 \(i\) 的次数。\(i^k\) 显然是 \(k\) 次的，后面 \((n-i+m-1)!\) 是 \(n-i+m-1\) 次的（\(n!\) 由 \(n\) 个有关于 \(n\) 的式子相乘，也就是 \(n\) 次），\((n-i)!\) 是 \(n-i\) 次的，\((m-1)!\) 是常数（式子里没有 \(i\)）。当然，前面的求和符号也得算上 \(1\) 次，所以最终这个式子是 \(k+m\) 次的。

根据拉格朗日插值，需要带入 \(k+m+1\) 个点带入多项式，现在上面的公式中的 \(n\) 就变成了次数 \(l=k+m\)。自行阅读一下 OI-wiki，发现我们只需要使用横坐标是连续整数的拉格朗日插值进行操作，也就是这个公式：

\[f(x)=\sum_{i=1}^{n+1}(-1)^{n-i+1}y_i \cdot \frac{\prod_{j=1}^{n+1}(x-j)}{(i-1)!(n-i+1)!(x-i)} \]

把 \(x\) 替换成 \(n\)，\(1 \to n+1\) 替换成 \(1\to l+1\)。接下来就是 \(y_i\) 的问题了，拉格朗日插值中的 \(y_i\) 不仅是单个 \(i_k\) 的贡献，\(i^k\) 的 \(m\) 阶前缀和，所以要预处理一下 \(y_i\)，最终就是这个问题的答案了。我们还需要预处理一下 \(l-i\) 的前后缀积、阶乘的逆元才能快速求解。

AC code：

#include <bits/stdc++.h>
#define int __int128
using namespace std;

const int mod = 1e9 + 7;
const int N = 2.5e6 + 5;
long long n, m, k, ans;
int a[N], inv[N], fac[N], pre[N], suf[N];

int ksm(int a, int b){
	int res = 1;
	while (b){
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

signed main(){
	cin >> n >> m >> k;
	if (n == 0) return cout <<"0", 0;
	int l = m + k + 1;
	for (int i = 1; i <= l; i++) a[i] = ksm(i, k);
	for (int j = 1; j <= m; j++){
		for (int i = 1; i <= l; i++) a[i] = (a[i] + a[i - 1]) % mod;//预处理 y_i
	}
	inv[0] = fac[0] = 1;
	for (int i = 1; i <= l; i++) fac[i] = fac[i - 1] * i % mod;
	inv[l] = ksm(fac[l], mod - 2);
	for (int i = l - 1; i >= 1; i--) inv[i] = (i + 1) * inv[i + 1] % mod;//预处理阶乘的逆元
	pre[0] = suf[l + 1] = 1;
	for (int i = 1; i <= l; i++) pre[i] = pre[i - 1] * (n - i) % mod;//预处理前后缀积
	for (int i = l; i >= 1; i--) suf[i] = suf[i + 1] * (n - i) % mod;
	for (int i = 1; i <= l; i++){
		ans = (ans + (a[i] * pre[i - 1] % mod * suf[i + 1] % mod * inv[i - 1] % mod * inv[l - i] % mod * (((l - i) & 1) ? -1 : 1) + mod) % mod) % mod;//拉格朗日插值
	}
	cout << ans;
	return 0;
}

G-CF2B

先来看怎样才能凑出一个 \(0\)，也就是 \(10^n\)。把 \(10\) 分解质因数，发现 \(10=2 \times 5\)，也就是这个数 \(2\) 和 \(5\) 次数的最小值为乘上这个数造成的 \(0\) 的数量。

考虑 dp，设 \(dp_{i,j}\) 为走到 \((i,j)\) 造成 \(0\) 的最小值，这一种写出来的代码很臭长，换一种想法 \(dp_{i,j,0/1}\) 表示第 \((i,j)\) 时 \(2/5\) 次数的最小值。解释一下正确性：因为最后答案时 \(2\) 的次数和 \(5\) 的次数的最小值，我们贪心地让一个数的次数越小越好，肯定就能取到最小值。

转移就是朴素的转移，\(dp_{i,j,0/1}=\min(dp_{i,j-1,0/1},dp_{i-1,j,0/1})+a_{i,j}\)，这里 \(0\) 和 \(1\) 的情况要分开操作。ans 也就是 \(\min(dp_{n,n,0},dp_{n,n,1})\)。

对于路径的查询，可以使用递归，ans 中取哪一个质因子小，就去递归这个质因子所经过的道路。从 \((n,n)\) 往 \((1,1)\) 走，记录当前走到下一步的方向和坐标，分类讨论一下：

• \(x=1\) 且 \(y=1\) 到达终点，直接输出然后开始回溯。
• \(x=1\)，只能往左边走，更换方向继续递归。
• \(y=1\)，同 \(x=1\)，只能往上走。
• 朴素情况，看哪一边的 dp 值满足 \((x,y)\) 是由 \((x_1,y_1)\) 转移过来的。

最后回溯时输出路径要特判一下 \((x,y)\) 不在 \((n,n)\)。

注意：需要特判一下图中是否有 \(0\)，如果有并且最终答案大于 \(1\)，那么最小值就等于 \(1\)，直接输出 \((1,1)\) 到 \((x_0,y_0)\) 和 \((x_0,y_0)\) 到 \((n,n)\) 的路径。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, ans, tmp;
int a[1005][1005][2], dp[1005][1005][2];

void print(int x, int y, int d){//递归找路径
	if (x == 1 && y == 1) return cout << (d == 0 ? 'D' : 'R'), void();
	if (x == 1) print(x, y - 1, 1);
	else if (y == 1) print(x - 1, y, 0);
	else if (dp[x][y][tmp] == dp[x - 1][y][tmp] + a[x][y][tmp]) print(x - 1, y, 0);
	else print(x, y - 1, 1);
	if (x != n || y != n) cout << (d == 0 ? 'D' : 'R');
}

int main(){
	cin >> n;
	for (int i = 1; i <= n; i++){
		for (int j = 1, k; j <= n; j++){
			cin >> k;
			if (k == 0) a[i][j][0] = a[i][j][1] = 1, tmp = i;
			else{
				while (k % 2 == 0) a[i][j][0]++, k /= 2;//记录 2 的次数
				while (k % 5 == 0) a[i][j][1]++, k /= 5;
			}
		}
	}
	memset(dp, 0x3f, sizeof(dp));
	dp[0][1][1] = dp[0][1][0] = dp[1][0][0] = dp[1][0][1] = 0;
	for (int k = 0; k < 2; k++){//2 5分开转移
		for (int i = 1; i <= n; i++){
			for (int j = 1; j <= n; j++) dp[i][j][k] = min(dp[i - 1][j][k], dp[i][j - 1][k]) + a[i][j][k];//转移
		}
	}
	ans = min(dp[n][n][0], dp[n][n][1]);
	if (tmp && ans > 1){//特判
		cout << "1\n";
		for (int i = 1; i < tmp; i++) cout << "D";
		for (int i = 1; i < n; i++) cout << "R";
		for (int i = tmp; i < n; i++) cout << "D";
		return 0;
	}
	cout << ans << endl;
	tmp = (dp[n][n][0] < dp[n][n][1] ? 0 : 1);
	print(n, n, 0);
	return 0;
}

AT_abc211 复盘

A

保留后 7 位

AC code:

#include <bits/stdc++.h>
using namespace std;

double a, b;

int main(){
	cin >> a >> b;
	printf("%.7lf", (a - b) / 3 + b);
	return 0;
}

B

随便拿个 map 搞搞

AC code:

#include <bits/stdc++.h>
using namespace std;

string a;
map<string, int> mp;

int main(){
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	cin >> a;
	mp[a] = 1;
	if (mp.size() != 4) cout << "No";
	else cout << "Yes";
	return 0;
}

C

朴素的 dp，考虑 \(dp_{i,j}\) 表示第 \(i\) 位取 \(j\) 个字符前缀合法的总数，转移方程就是 \(dp_{i,j}=dp_{i, j}+dp_{i-1,j-1}\)。在转移之前，所有的 \(dp_{i,j}\) 都得继承 \(dp_{i-1,j}\) 的值，相当于一个前缀和。

进一步，发现可以把第一位压缩掉，变成一个很简单的式子 \(dp_{j}=dp_j + dp_{j-1}\) 这里 \(j\) 表示当前字符。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 1e9 + 7;
string s;
map<char, int> mp;
int dp[10];

signed main(){
	cin >> s;
	s = ' ' + s;
	mp['c'] = 1, mp['h'] = 2, mp['o'] = 3, mp['k'] = 4, mp['u'] = 5, mp['d'] = 6, mp['a'] = 7, mp['i'] = 8;
	dp[0] = 1;
	for (int i = 1; i < s.size(); i++){
		dp[mp[s[i]]] = (dp[mp[s[i]]] + dp[mp[s[i]] - 1]) % mod;
	}
	cout << dp[8];
	return 0;
}

D

最短路计数双倍经验。

记录一下到每个点的最短路 \(dis\)，和最短路的数量 \(dp\)。按照 dijkstra 的思路（其实可以用 bfs）找到下一个节点的距离有两种情况：

• 下一个点 \(v\) 的最短距离比当前节点 \(u\) 的最短距离加 \(1\) 大，那么 \(dp_{v}=dp_u\) 直接继承，再更新一下最短距离，加入队列。
• 下一个点 \(v\) 的最短距离与当前节点 \(u\) 的最短距离加 \(1\) 相等，直接在 \(dp_v\) 上面加上到 \(u\) 最短路条数 \(dp_u\)。

最终答案就是 \(dp_n\)，注意在加的时候要模 \(10^9+7\)。

AC code:

#include <bits/stdc++.h>
#define pii pair<int, int>
using namespace std;

const int mod = 100003;
int n, m;
int dp[1000005], dis[1000005];
vector<int> g[1000005];

void bfs(int x){
    priority_queue<pii, vector<pii>, greater<pii>> q;
    memset(dis, 0x3f, sizeof(dis));
    q.push({dis[x] = 0, x});
    dp[x] = 1;
    while (!q.empty()){
        int u = q.top().second; q.pop();
        for (int i = 0; i < g[u].size(); i++){
            int v = g[u][i];
            if (dis[u] + 1 < dis[v]){
                dp[v] = dp[u];
                dis[v] = dis[u] + 1;
                q.push({dis[v], v});
            }
            else if (dis[u] + 1 == dis[v]) dp[v] = (dp[v] + dp[u]) % mod;
        }
    }
}

int main(){
    cin >> n >> m;
    for (int i = 1, u, v; i <= m; i++){
        cin >>u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    bfs(1);
    for (int i = 1; i <= n; i++) cout << dp[i] << "\n";
    return 0;
}

E

很明显是 dfs，枚举这个位置填充了没有，但是不是一般的 dfs，它没有起点和终点，那么考虑一次性填整个图。

稍微魔改一下 dfs，直接传入当前矩阵状态，判断是否合法，再去看每一个点能否填上红色，如果能就填上去试一遍，不能就不管它。

之后就是细节问题：

• 对于传参，可以使用 vector，比字符串数组方便优雅。

• 对于判断能否填上红色，判断这个点周围是否有红色，如果有才能填。特别的，如果当前图上没有红色，那么可以随便填。

• 在填完红色之后还要用不填红色继续判断，这里要将白色节点染成黑色，因为我们这时整个图去递归，如果染成白色的话在下一层还会回来染这个点，然后就死循环了。

• 每次 dfs 的时候找到第一个合法的点染色操作完之后就可以 return 了，因为剩下的点的情况都已经被当前点两种分类讨论处理掉了。

AC code:

#include <bits/stdc++.h>
using namespace std;

const int dx[4] = {0, 1, 0, -1};
const int dy[4] = {1, 0, -1, 0};
int n, k, ans;
vector<string> s(10);

void dfs(vector<string> s){//直接传一整个图
	int cnt = 0;
	for (int i = 0; i < n; i++){
		for (int j = 0; j < n; j++) cnt += (s[i][j] == 'o');
	}
	if (cnt == k) return ans++, void();//判断是否符合条件
	for (int i = 0; i < n; i++){
		for (int j = 0; j < n; j++){
			if (s[i][j] != '.') continue;
			if (cnt){//判断是否能染成红色
				bool flag = 0;
				for (int l = 0; l < 4; l++){
					int nx = i + dx[l], ny = j + dy[l];
					if (nx >= 0 && nx < n && ny >= 0 && ny < n && s[nx][ny] == 'o') flag = 1;
				}
				if (!flag) continue;
			} 
			s[i][j] = 'o';//染成红色
			dfs(s);
			s[i][j] = '#';//染成黑色，避免死循环
			dfs(s);
			return ;
		}
	}
}

int main(){
	cin >> n >> k;
	for (int i = 0; i < n; i++) cin >> s[i];
	dfs(s);
	cout << ans;
	return 0;
}

F

扫描线？

先将问题简化一下，判断这个点在多少个矩形之内？这样只需要给每一条竖着的边打上一个标记，用树状数组维护一下就好。

这种不规则的也差不多，难就难在如何给每个点打上标记 和 如何维护纵坐标。这里用到一个很巧妙的标记技巧，用 \(1\) 和 \(-1\) 轮流标记这些点，再加上题目给的按一横一竖的方式输入这些边，这样就能做到分辨后面的点属于图形内……吗？不对，如果图形是下面这种，然后第一次标记的点是 \((2,1)\)，模拟一下发现 \(x=1\) 到 \(x=2\) 之间的点是不在图形内的，而 \(x=2\) 右边的点是在图形内的，显然是不对的。考虑第一次标记最左边的边，这样似乎就避免了这个问题。

为什么能避免？那还得说如何标记一条边。善良的题面又给我们了点是按顺序输入的，那么我们可以规定一条竖着的边是由横坐标、下面的点的纵坐标、上面的点的纵坐标和往后是不是在图形内，最后这个标记我们统一使用这条边下面那个点的标记，因为是轮流标记加上有顺序而且它还得是一个封闭图形，所以必定是一条边标记为 \(1\)，与之相邻的边标记为 \(-1\)。

然后 sort 一下，把所有边从左到右排一遍，处理查询的时候也是从左到右排一遍，这样方便我们使用双指针。这里按照上面矩形的思路，构造一个树状数组，存的是什么呢？肯定是纵坐标上的值。很好理解，存横坐标没有意义（直接前缀和）而纵坐标上每条边到哪里我们又不知道，所以存纵坐标。细节上，双指针很好实现，对于每一条边我们都要挪动查询的点的横坐标，挪到最后一个在这条边左边的点，记录答案。

对于查询答案，直接看当前节点纵坐标的值加起来。那更新呢？我们有个朴素的想法，开两维，第一维对应一个横坐标。这样肯定是不行的，再看回前面竖着的边的性质——一个为正一个为负，那就可以直接在纵坐标上加上这条边的标记（相当于前缀和），而这个标记肯定会在下一条边的时候清理掉不在矩形内的部分，而没清理掉的会继续前缀和往后走。

代码细节，在处理坐标的时候可以集体加一，把 \((0,0)\) 挪到 \((1,1)\) 上；询问要离线处理，记得打上 \(id\)。

AC code：

#include <bits/stdc++.h>
#define pii pair<int, int>
using namespace std;

int n, m, q;
int xx[100005], yy[100005], w[100005], ans[100005], c[100005];
struct side{
    int x, ya, yb, val;
};
struct que{
    int x, y, id;
};
vector<side> v;
vector<que> v1;

bool cmp(side x, side y){
    if (x.x == y.x) return x.ya < y.ya;
    return x.x < y.x;
}

bool cmp1(que x, que y){
    if (x.x == y.x) return x.y < y.y;
    else return x.x < y.x;
}

int lowbit(int x){
    return x & -x;
}

void update(int x, int k){
    while (x <= 1e5) c[x] += k, x += lowbit(x);
}

int query(int x){
    int res = 0;
    while (x) res += c[x], x -= lowbit(x);
    return res;
}

int main(){
    cin >> n;
    for (int i = 1; i <= n; i++){
        cin >> m;
        int minx = 0;
        for (int j = 0; j < m; j++){
            cin >> xx[j] >> yy[j];
            xx[j]++, yy[j]++;//好操作，往后往上挪一个
            if (make_pair(xx[j], yy[j]) < make_pair(xx[minx], yy[minx])) minx = j;//最左边就保证了这条边往右一定在图形内
        }
        int val = 1;
        for (int j = 0; j < m; j++){
            int tmp = (j + minx) % m;//要保证取轮流标，不然相邻两条边的性质就没了
            w[tmp] = val, val = -val;//轮流标记是正还是负
        }
        for (int j = 0; j < m; j += 2){
            if (yy[j] < yy[j + 1]) v.push_back((side){xx[j], yy[j], yy[j + 1], w[j]});
            else v.push_back((side){xx[j], yy[j + 1], yy[j], w[j + 1]});//push下面那个点的标记
        }
    }
    sort(v.begin(), v.end(), cmp);
    v.push_back((side){(int)1e5 + 1, 1, 1, 0});
    cin >> q;
    for (int i = 1; i <= q; i++){
        cin >> xx[i] >> yy[i];
        xx[i]++, yy[i]++;
        v1.push_back((que){xx[i], yy[i], i});//离线操作，记录下id
    }
    sort(v1.begin(), v1.end(), cmp1);
    int pos = 0;
    for (int i = 0; i < v.size(); i++){
        int x = v[i].x, ya = v[i].ya, yb = v[i].yb, val = v[i].val;
        for (; v1[pos].x < x && pos < v1.size(); pos++) ans[v1[pos].id] = query(v1[pos].y);//直接查询
        update(ya, val), update(yb, -val);//直接在纵坐标上更新，相邻两个点标记相反
    }
    for (int i = 1; i <= q; i++) cout << ans[i] << endl;
    return 0;
}

G

首先我们要明确一个结论：

一个有向图如果是强连通的，那么边数必定小于等于点数

很好理解，如果把所有点串成一个环，那肯定是强连通的。

考虑题目要求。首先强连通图肯定满足；更少一点，比如说如果这些点连上边后能变成一棵树，并且满足条件，当然这也是最小的（得保证这些点联通）。

现在问题就转化成了原图能不能变成一棵树。成为一棵树的必要条件就是不能有环，有环就相当于我是我自己的父亲，肯定不满足（带回原题中，如果有环，那么肯定需要比一棵树需要的边数多至少一个，肯定没有强连通图优）。剩下的一定满足吗？由拓扑排序（类似这题）可以得到唯一的拓扑序，也就是满足答案的建边顺序。

这里对拓扑排序不做过多赘述，之后是细节：

• 这里分很多个连通块，要对每个连通块进行判断。
• 对于维护连通块大小（也就是点数），不能用 dfs（可能有一些点遍历不到）可以用并查集来维护每一个连通块。
• 对于求最后的贡献，可以直接统计有多少个连通块满足可以构成一棵树，减去它们就好了。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, m;
int vis[100005], fa[100005], ind[100005], d[100005];
vector<int> g[100005];
map<int, int> mp;

int find(int x){//用并查集维护连通块
	return (x == fa[x] ? x : fa[x] = find(fa[x]));
}

void merge(int x, int y){
	fa[find(y)] = find(x);
}

void tuopu(){//拓扑
	queue<int> q;
	for(int i = 1; i <= n; i++){
		if(ind[i] == 0) q.push(i), vis[i] = 1;
	}
	while(!q.empty()){
		int u = q.front(); q.pop();
		for(int i = 0; i < g[u].size(); i++){
            int v = g[u][i];
			ind[v]--;
			if(ind[v] == 0){
				q.push(v);
				vis[v] = vis[u] + 1;
			}
		}
	}
}

int main(){
	cin >> n >> m;
	for (int i = 1; i <= n; i++) fa[i] = i;
	for (int i = 1, u, v; i <= m; i++){
		cin >> u >> v;
		g[u].push_back(v);
        ind[v]++;
		merge(u, v);
	}
    tuopu();
    for(int i = 1; i <= n; i++) {
		if(vis[i] == 0) d[find(i)] = true;//不在拓扑序里面，肯定有环
	}
	for(int i = 1; i <= n; i++){
        if(!d[find(i)]) mp[find(i)] = 1;//如果这个连通块中没有环，记录减1的次数
    }
	cout << n - mp.size();//减去能构成树的
	return 0;
}

AT_abc212 复盘

A

if

AC code:

#include <bits/stdc++.h>
using namespace std;

int a, b;

int main(){
	cin >> a >> b;
	if (a == 0) cout << "Silver";
	else if (b == 0) cout << "Gold";
	else cout << "Alloy";
	return 0;
}

B

C

可以先把 \(b\) 排序，然后对于每一个 \(a_i\) 在 \(b\) 中二分一下，找到第一个比它小和大的数，然后判断一下

注意：特判一下边界

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, m, ans = 1e18;
int a[200005], b[200005];

signed main(){
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= m; i++) cin >> b[i];
	sort(b + 1, b + m + 1);
	for (int i = 1; i <= n; i++){
		int pos = lower_bound(b + 1, b + m + 1, a[i]) - b;
		if (pos == 1) ans = min(ans, abs(a[i] - b[pos]));
		else ans = min(ans, min(abs(a[i] - b[pos]), abs(a[i] - b[pos - 1])));
	}
	cout << ans;
	return 0;
}

D

对于操作 2，直接打上一个 lazytag，最后输出的时候加上即可。

对于操作 3，直接输出优先队列队头 + lazytag 的值。

对于操作 1，在优先队列中加入 \(x\) 减去 lazytag，不然后面会重复加一遍。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, opt, x, add;
priority_queue<int, vector<int>, greater<int>> q;

signed main() {
	cin >> n;
	while (n--) {
		cin >> opt;
		if (opt == 1) {
			cin >> x;
			q.push(x - add);
		}
        else if (opt == 2) {
			cin >> x;
			add += x;
		}
        else if (opt == 3) {
			cout << q.top() + add << endl;
			q.pop();
		}
	}
	return 0;
}

E

考虑 dp，设 \(dp_{i,j}\) 表示第 \(i\) 轮走到 \(j\) 的方案数，basecase 为 \(dp_{0,1}=1\)，ans 为 \(dp_{k,1}\)。

转移方程不显然，考虑没有删边的情况，\(dp_{i,j}=\sum_{j=1}^ndp_{i-1,j}-dp_{i-1,j}\)，那么加上删边减去的贡献，也就是 \(\sum_{v\in g_u} dp_{i-1,v}\)，最后得到一条屎一样的式子：

\[dp_{i,j}=\sum_{j=1}^ndp_{i-1,j}-dp_{i-1,j}-\sum_{v\in g_u} dp_{i-1,v} \]

AC code:

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, m, k;
int dp[5005][5005];
vector<int> g[5005];

signed main(){
	cin >> n >> m >> k;
	for (int i = 1, u, v; i <= m; i++){
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dp[0][1] = 1;//basecase
	for (int i = 1; i <= k; i++){
		int sum = 0;
		for (int j = 1; j <= n; j++) sum += dp[i - 1][j];//第一项
		for (int j = 1; j <= n; j++){
			dp[i][j] = sum - dp[i - 1][j];//第二项
			for (int k = 0; k < g[j].size(); k++){//第三项
				int v = g[j][k];
				dp[i][j] -= dp[i - 1][v];
			}
			dp[i][j] %= mod;
		}
	}
	cout << dp[k][1];//ans
	return 0;
}

AT_abc217 复盘

A

非常水

AC code:

#include <bits/stdc++.h>
using namespace std;

string s1, s2;

int main(){
	cin >> s1 >> s2;
	if (s1 < s2) cout << "Yes";
	else cout << "No";
	return 0;
}

B

还是非常水，随便拿 map 搞搞

AC code:

#include <bits/stdc++.h>
using namespace std;

string s1, s2, s3;
map<string, int> mp;

int main(){
	cin >> s1 >> s2 >> s3;
	mp[s1] = 1, mp[s2] = 1, mp[s3] = 1;
	string a = "ABC", b = "ARC", c = "AGC", d = "AHC";
	if (mp[a] == 0) cout << a;
	else if (mp[b] == 0) cout << b;
	else if (mp[c] == 0) cout << c;
	else if (mp[d] == 0) cout << d;
	return 0;
}

C

依旧很水，直接映射一下，甚至不用离散化

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
int a[200005], b[200005];

int main(){
	cin >> n;
	for (int i = 1; i <= n; i++){
		cin >> a[i];
		b[a[i]] = i;
	}
	for (int i = 1; i <= n; i++) cout << b[i] << " ";
	return 0;
}

D

有点难度，但不多。很容易想到二分一下找上界和下界，所以要维护一个数组使它插入的时候自动排好序，用 set

注意：用 set 的时候一定要用自带的二分 st.lower_bound 不然会 TLE

警钟敲烂！！！！

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, q;
set<int> st;

signed main(){
    cin >> n >> q;
    st.insert(0), st.insert(n);
    for (int i = 1, opt, x; i <= q; i++){
        cin >> opt >> x;
        if (opt == 1) st.insert(x); 
        else{
            auto it = st.lower_bound(x);
            cout << *it - *(--it) << endl;
        }
    }
    return 0;
}

E

比 D 水，直接拿一个优先队列和普通队列处理一下就好了

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
queue<int> q;
priority_queue<int, vector<int>, greater<int>> q1;

int main(){
	cin >> n;
	for (int i = 1, opt, x; i <= n; i++){
		cin >> opt;
		if (opt == 1){
			cin >> x;
			q.push(x);
		}
		else if (opt == 2){
			if (q1.empty()) cout << q.front() << endl, q.pop();
			else cout << q1.top() << endl, q1.pop();
		}
		else{
			while (!q.empty()) q1.push(q.front()), q.pop();
		}
	}
	return 0;
}

F

”遇到组合计数的题要么是数学，要么是 dp。“

一开始见到这题感觉是数学，但是这是区间 dp。定义 \(dp_{i,j}\) 表示把 \([i,j]\) 完全消掉的方案数。

不难想到转移，如果 \(l\) 和 \(r\) 是好朋友，那么 \(dp_{l,r}=dp_{l + 1, r - 1}\)。考虑一般情况，枚举断点 \(k\)，如果 \(k\) 和 \(r\) 也是朋友关系，就可以做到先把 \([l,k-1]\) 的消掉，再消 \([k + 1,r-1]\) 最后再把 \(k,r\) 消掉，也就是 \(dp_{l,r}=dp_{l, k-1} \times dp_{k + 1,r - 1}\)，但是这种没考虑删的顺序，所以还要乘上一个 \(C_{\frac{r - l + 1}{2}}^{\frac{r-k+1}{2}}\)。注意不是阶乘，因为这两个区间内的先后顺序是确定的，只是在两个区间混起来消除的时候考虑这一次消左边还是消右边。

注意在 \(dp\) 初始化时要 \(dp_{u,v}=dp_{v,u}=1\)，不然在后面枚举断点的时候可能会出现 \(k=r-1\) 的情况，然后计算的时候就 \(k+1>r-1\) 了，但是还是算方案数的，所以反向也要记录一下。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, m;
int dp[405][405], vis[405][405], c[405][405];

signed main(){
    for (int i = 0; i <= 400; i++){
        for (int j = 0;  j <= i; j++){
            if (i == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }
    cin >> n >> m;
    for (int i = 1, u, v; i <= m; i++){
        cin >> u >> v;
        if ((v - u + 1) % 2) continue;
        vis[u][v] = 1;
        if (u + 1 == v) dp[u][v] = dp[v][u] = 1;
    }
    for (int len = 2; len <= 2 * n; len += 2){
        for (int l = 1; l + len - 1 <= 2 * n; l++){
            int r = l + len - 1;
            if (vis[l][r]) dp[l][r] = dp[l + 1][r - 1];
            for (int k = l + 2; k < r; k += 2){
                if (vis[k][r]) dp[l][r] = (dp[l][r] + dp[l][k - 1] * dp[k + 1][r - 1] % mod * c[len / 2][(r - k + 1) / 2] % mod) % mod;
            }
        }
    }
    cout << dp[1][2 * n];
    return 0;
}

G

比 F 简单一些。前置知识：斯特林数。

先来考虑简单情况，把 \(n\) 个数分成 \(m\) 组有多少种情况？

可以定义 \(dp_{i,j}\) 表示第 \(i\) 个数之前分了 \(j\) 组有多少种情况。

转移分两种讨论：

• \(i\) 单独开一组新的：\(dp_{i,j}=dp_{i-1,j-1}\)。

• 把 \(i\) 放到前面的几组中：\(dp_{i,j}=dp_{i-1,j} \times j\)。乘上 \(j\) 表示可以放到前 \(j\) 组，每组 \(dp_{i-1,j}\) 种情况。

回到原题，因为有了模数的限制，问题肯定出在放到前 \(j\) 组的地方，那么要乘上多少呢？就是除了放了模数相同的数的组里。而我们已经知道前 \(i-1\) 个数中与 \(i\) 同余的数肯定不在一个格子内，而有 \(\lfloor \frac{i-1}{m}\rfloor\) 个与 \(i\) 同余的数，所以有 \(j-\lfloor \frac{i-1}{m}\rfloor\) 组是合法的，可得最后式子为：

\[dp_{i,j}=dp_{i-1,j-1}+dp_{i-1,j} \times (j-\lfloor \frac{i-1}{m}\rfloor) \]

还有一点，在转移的时候记得将合法组数和 \(0\) 取一个 \(\max\)，肯定不能取负的组数嘛。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, m;
int dp[5005][5005];

signed main(){
    cin >> n >> m;
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= i; j++){
            dp[i][j] = (dp[i][j] + dp[i - 1][j - 1]) % mod;
            dp[i][j] = (dp[i][j] + dp[i - 1][j] * max((j - (i - 1) / m), 0ll)) % mod;
        }
    }
    for (int i = 1; i <= n; i++) cout << dp[n][i] << endl;
    return 0;
}

AT_abc219 复盘

A

直接上 if 大法

AC code:

#include <bits/stdc++.h>
using namespace std;

int x;

int main(){
	cin >> x;
	if (x < 40) cout << 40 - x;
	else if (x >= 40 && x < 70) cout << 70 - x;
	else if (x >= 70 && x < 90) cout << 90 - x;
	else cout << "expert";
	return 0;
}

B

暴力字符串拼接

AC code:

#include <bits/stdc++.h>
using namespace std;

string s[5], t, ans;

int main(){
	cin >> s[1] >> s[2] >> s[3] >> t;
	for (int i = 0; i < t.size(); i++) ans += s[t[i] - '0'];
	cout << ans;
	return 0;
}

C

好像直接写一个 \(cmp\) 也可以

拿一个 map 映射新字符对应着哪一个旧字符。询问的时候转换一下新旧字符，再拿个 map 映射一下，最后输出

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
string s, t;
map<char, char> mp;
map<string, string> pre;
vector<string> v;

int main(){
	cin >> s;
	for (int i = 0; i < s.size(); i++) mp[s[i]] = i + 'a';
	cin >> n;
	for (int i = 1; i <= n; i++){
		cin >> t;
		string tmp = t;
		for (int i = 0; i < t.size(); i++) tmp[i] = mp[t[i]];
		v.push_back(tmp);
		pre[tmp] = t;
	}
	sort(v.begin(), v.end());
	for (int i = 0; i < n; i++) cout << pre[v[i]] << endl;
	return 0;
}

D

很明显是一个 dp 题。

按照朴素的想法，\(dp_{i,j,k}\) 表示前 \(i\) 个盒饭 \(j\) 个 a 种， \(k\) 个 b 种，很明显这样会 RE。

转换一下 \(dp_{i,j,k}\) 表示前 \(i\) 个盒饭大于等于 \(j\) 个 a 种，大于等于 \(k\) 个 b 种，这样子只用开到 \(300 \times 300 \times 300\) 就够了。

转移分两种：

• 取 \(i - 1\) 个盒饭就已经满足要求，\(dp_{i,j,k}=dp_{i-1,j,k}\)
• 取第 \(i\) 个盒饭，\(dp_{i,j,k}=\min(dp_{i,j,k}, dp_{i-1,j-a[i],k-b[i]}+1)\)

basecase 很好想，肯定就是 \(dp_{0,0,0}=0\)。ans 就是 \(dp_{n,x,y}\)

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, x, y;
int a[305], b[305], dp[305][305][305];

int main(){
	cin >> n >> x >> y;
	for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
	memset(dp, 0x3f, sizeof(dp));
	dp[0][0][0] = 0;//basecase
	for (int i = 1; i <= n; i++){
		for (int j = 0; j <= x; j++){
			for (int k = 0; k <= y; k++){
				if (dp[i - 1][j][k] != 0x3f3f3f3f) dp[i][j][k] = dp[i - 1][j][k];//直接满足条件
				dp[i][j][k] = min(dp[i][j][k], dp[i - 1][max(j - a[i], 0)][max(k - b[i], 0)] + 1);//转移，记得特判一下边界
			}
		}
	}
	cout << (dp[n][x][y] == 0x3f3f3f3f ? -1 : dp[n][x][y]);
	return 0;
}

E

数据范围很容易想到状压，但又很容易误导成状压 dp。

只需要枚举那个点在护城河内，在去判断不合法的情况。第 4、5 种情况已经被排除了，只需要判断前三种情况。

第一种很好判断，第二种也只需要去判一下连通块是否只有一个，而第三种就有点难度了。我们发现，如果状压出来的护城河由两条的话肯定是围成了一个类似于大圆套小圆的结构，护城河包裹的是圆环，而中间那部分在状压中是没有被包裹的，这就只需要判断是否有一块没有选中的点是走不到边缘的，如果有，那一定是被圆环包裹住了，也就是不合法的情况。

最后统计答案。

第二种：

第三种：

AC code:

#include  <bits/stdc++.h>
using namespace std;

const int dx[4] = {0, 1, 0, -1};
const int dy[4] = {1, 0, -1, 0};
int n = 4, ans;
int a[5][5], b[5][5], vis[5][5];

int dfs1(int x, int y){//找被护城河围起来了但不是城内的区域
    if (x <= 0 || x > n || y <= 0 || y > n) return 1;
    if (b[x][y]) return 0;
    vis[x][y] = 1;
    int flag = 0;
    for (int i = 0; i < 4; i++){
        int nx = x + dx[i], ny = y + dy[i];
        if (vis[nx][ny]) continue;
        flag |= dfs1(nx, ny);//这一个点所连接的点中只要有一个能走出去就行
    }
    return flag;
}

void dfs(int x, int y){//找连通块
    vis[x][y] = 1;
    for (int i = 0; i < 4; i++){
        int nx = x + dx[i], ny = y + dy[i];
        if (nx > 0 && nx <= n && ny > 0 && ny <= n && vis[nx][ny] == 0 && b[nx][ny] == 1) dfs(nx, ny);
    }
}

int main(){
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= n; j++) cin >> a[i][j];
    }
    for (int k = 1; k < (1 << (n * n)); k++){
        for (int i = 0; i < n * n; i++) b[i / n + 1][i % n + 1] = 1 & (k >> i);//状态中每一位对应着矩阵中哪一个地方
        memset(vis, 0, sizeof(vis));
        int flag = 1, cnt = 0;
        for (int i = 1; i <= n && flag; i++){
            for (int j = 1; j <= n && flag; j++){
                if (a[i][j] == 1 && b[i][j] == 0) flag = 0;//第一种情况
                else if (b[i][j] == 0 && !vis[i][j]) flag = dfs1(i, j);//第三种情况，有环
                else if (b[i][j] == 1){
                    if (cnt && !vis[i][j]) flag = 0;//第二种情况，有好多个连通块
                    else dfs(i, j), cnt++;
                }
            }
        }
        if (flag) ans++;
    }
    cout << ans;
    return 0;
}

F

先模拟一遍样例，我们发现在第二次操作的时候画出来的路径就是第一次操作的路径往一个方向偏移了一个值，也就是每一次的起点都偏移了相同的 \((x,y)\) 值。

具体的，设第一轮运动（\(x_0=0,y_0=0\)）的点集为 \(P=\{(x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)\}\)，显然增量 \(\Delta x=x_n-x_0=x_n\) 同理 \(\Delta y=y_n\)。

接着我们可以再手搓一点样例出来，发现路径中的每一个点也是相较于上一次操作偏移了 \((\Delta x,\Delta y)\)。

这里就可以特判骗一点分了：如果 \(\Delta x = 0\) 且 \(\Delta y = 0\)，直接输出一轮有多少个点。

虽然这个结论看起来很没用，实际上这对之后计算很有帮助。很容易发现我们得减去重复的值，再加上增加的值。接下来就开始抽象了。

对于重复点的计算，因为我们有上面“每一次的增量都是固定的”这一说法，那重复的点也是固定的，带入一次函数，每组重复的点组成的直线的斜率一定是 \(\frac{\Delta y}{\Delta x}\)（这里增量固定，所以一组重复的点一定是在一条直线上的）。

但是我们发现重复次数依旧不好计算，那我们只能算贡献了，分成两种点：

• 到一个时间以后都没有贡献。同一条直线上前一个点走过的路被当前点走过了，贡献就是这两个点之间要走的次数。具体的，\((x_i,y_i)=(x_j+d\Delta x,y_j+d\Delta y)\) 时，他们的贡献就是 \(d=\frac{x_i-x_j}{\ \Delta x}\)（每一次 \(x\) 运动 \(\Delta x\) 个单位距离）。
  

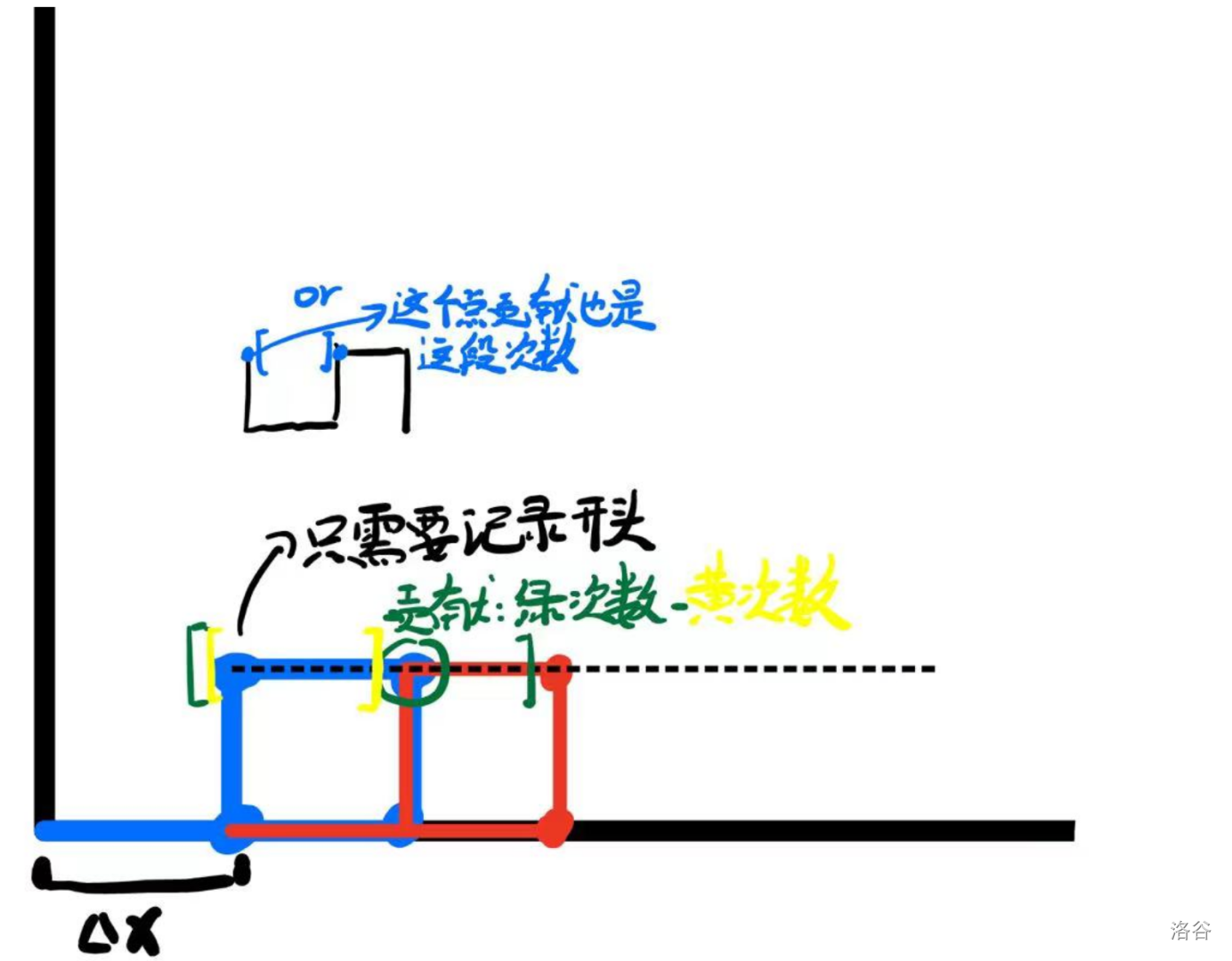
• 一直有贡献。每条直线最后一个点（最远的那个点）移动的时候肯定是没有点拦着的，直接让 \(ans\) 加上运动次数 \(k\) 就好了。
  

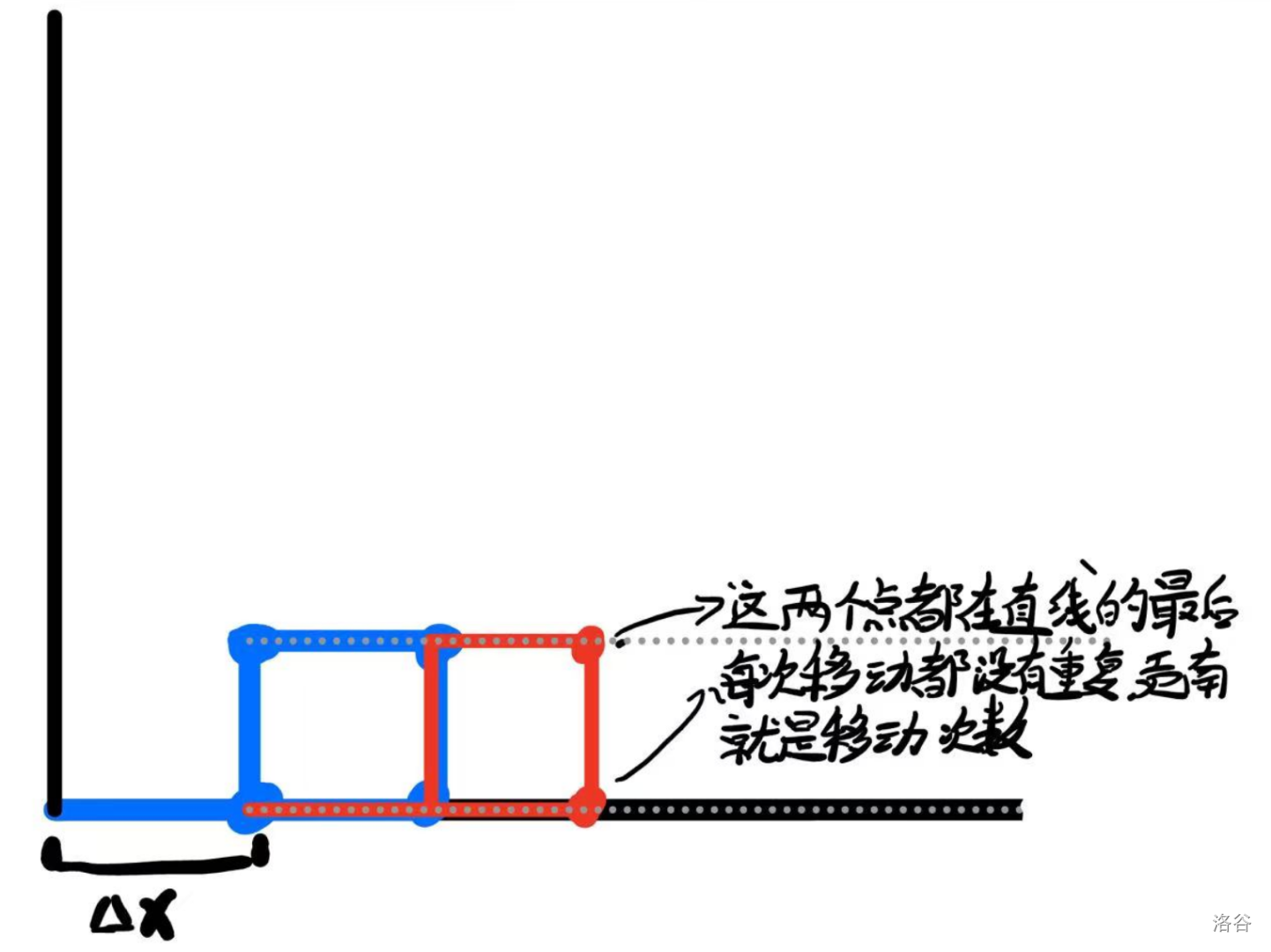
事实上，只要统计第一次移动出现过的点的贡献（第一种），其他的点要么是以后都有贡献的点，要么是已经不可能再有贡献的点了。

这道题做完了……吗？现在只剩最后一个问题，怎么记录同一条直线？稍微学过高中直线方程的都知道，只要知道斜率、一个点，就能确定一条直线，这个点就可以选在这条直线出现的第一个点，也就是 \((x \bmod \Delta x,y\bmod \Delta y)\)，直接用 map 去存这个点到所在直线上的点运动的次数，然后给这些次数排个序再去统计答案。

为了便于计算我们需要更改下不满足条件的 \((\Delta x,\Delta y)\):

• 当 \(\Delta x=0\) 时，交换 \(\Delta x\) 和 \(\Delta y\)（在模的时候便于操作），记得交换每一个点的 \((x,y)\)。
• 当 \(\Delta x< 0\) 时，直接取反 \(\Delta x\)，同时取反每一个点的 \(x\)。

上面我们交换了 \(\Delta x=0\) 的时候的这两个值，那么 \(y \bmod \Delta y\) 时我们只能根据斜截式方程去转化一下，变成 \(y-\Delta y \cdot \frac{x - x \bmod \Delta x}{\Delta x}\)，之后正常操作。

AC code:

#include  <bits/stdc++.h>
#define int long long
using namespace std;

int k, x, y, ans;
string s;
vector<pair<int, int>> v;

signed main(){
    cin >> s >> k;
    v.push_back({x, y});//不要忘记原点
    for (int i = 0; i < s.size(); i++){//统计第一次的路径
        if (s[i] == 'U') y--;
        if (s[i] == 'D') y++;
        if (s[i] == 'L') x--;
        if (s[i] == 'R') x++;
        v.push_back({x, y});
    }
    if (x == 0 && y == 0){//特判原地不动
        map<pair<int, int>, int> mp;
        for (int i = 0; i < v.size(); i++) mp[v[i]] = 1;
        return cout << mp.size(), 0;
    }
    if (x == 0){//特判x = 0
        swap(x, y);
        for (int i = 0; i < v.size(); i++) swap(v[i].first, v[i].second);//记得掉换
    }
    if (x < 0){//特判 x < 0
        x = -x;
        for (int i = 0; i < v.size(); i++) v[i].first = -v[i].first;
    }
    map<pair<int, int>, vector<int>> mp;
    for (int i = 0; i < v.size(); i++){
        int nx = (v[i].first % x + x) % x;//记得这样取模，避免出现负数炸掉
        int ny = (v[i].second - y * (v[i].first - nx) / x);//斜截式方程
        mp[{nx, ny}].push_back((v[i].first - nx) / x);//记录从直线第一个点经过多少次操作能来到当前节点，也就是贡献
    }
    for (auto it : mp){
        sort(it.second.begin(), it.second.end());//次数排序
        for (int i = 0; i < it.second.size() - 1; i++) ans += min(k, it.second[i + 1] - it.second[i]);//统计两个点之间走的次数
        ans += k;//一直都有贡献的点
    }
    cout << ans;
    return 0;
}

G

根号分治，简单来说就是小于某一个值和大于某个值分开来做。

这题如果用暴力就是 \(n^2\) 级别的，会炸。在想优化的过程中，我们发现如果把所有要修改的点都打上标记的话，还是在 \(n^2\) 级别的，但是变成了修改 \(O(1)\)，查询 \(O(n)\) 的东西，这种跟分块有点类似——就是根号分治。我们的目的就是平摊复杂度，修改 \(\sqrt n\)，查询 \(\sqrt{n}\)。

如何分块？只要把点分成两类，重点和轻点——重点代表所连边数大于 \(\sqrt{m}\)，轻点则相反。

轻点就可以直接在操作的时候暴力修改，而重点就可以打一个类似于线段树的 lazytag，包含一个当前颜色 color 和修改时间 time。注意，这里的 tag 是指这个重点放出的颜色的 color 和 time，而不是这个点最终颜色。

还需要预处理一下，再建一个图，只由轻点和所连接的重点构成。

具体操作时，先把要修改的那个点还原出来，也就是把与它邻接的重点的 tag 扒出来，找到修改时间最晚并且晚于当前节点修改时间的重点，覆盖掉当前节点。

并更新当前节点覆盖别的节点的 time。然后分治重点和轻点，轻点直接更新，重点打上一个 tag，等到下次要用到这个重点的时候再按上一个步骤中的操作还原到需要的节点上。

对于复杂度的证明，重点不超过 \(\sqrt{m}\) 个，于是还原节点最多 \(O(\sqrt{m})\)；打上 tag 的复杂度为 \(O(1)\)；轻点所连的边不超过 \(\sqrt{m}\)，更新一次复杂度也不超过 \(\sqrt{m}\)。

预处理阶段，只连接轻点的重点，不超过 \(n \sqrt{n}\)；最后输出操作也不超过 \(n \sqrt{m}\)。总复杂度在 \(n\sqrt{n}\) 级别，可以过。

AC code:

#include  <bits/stdc++.h>
using namespace std;

int n, m, q, len;
int col[200005], tim[200005];//最终答案和标记时间
int col1[200005], tim1[200005];//重点放出的color和放出时间
vector<int> g[200005], e[200005];//完整的图和每一个轻点连向重点的图

int find(int x){//找到更新时间最晚的重点
    int mxt = tim[x], tmp = col[x];//先记录当前节点更新时间，便于后面判断是否晚于当前节点
    for (int i = 0; i < e[x].size(); i++){
        int v = e[x][i];
        if (mxt < tim1[v]) mxt = tim1[v], tmp = col1[v];
    }
    return tmp;
}

int main(){
    cin >> n >> m >> q;
    len = sqrt(m);
    for (int i = 1; i <= n; i++) col[i] = i;
    for (int i = 1, u, v; i <= m; i++){
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for (int i = 1; i <= n; i++){
        if (g[i].size() < len) continue;
        for (int j = 0; j < g[i].size(); j++) e[g[i][j]].push_back(i);//只记录轻点连向重点的边，达到 根号 m 的复杂度
    }
    for (int _ = 1, x; _ <= q; _++){
        cin >> x;
        col[x] = find(x), tim[x] = _;
        if (g[x].size() >= len) col1[x] = col[x], tim1[x] = _;//重点打上lazytag
        else{
            for (int i = 0; i < g[x].size(); i++) col[g[x][i]] = col[x], tim[g[x][i]] = _;//轻点直接更新
        }
    }
    for (int i = 1; i <= n; i++) cout << find(i) << " ";//跟上面还原 col[x] 一个道理
    return 0;
}

AT_abc221 复盘

A

water，但我挂了。pow 回转科学计数法！！！

警钟敲烂！！！

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int a, b, ans = 1;

signed main(){
	cin >> a >> b;
	for (int i = 1; i <= a - b; i++) ans *= 32;
	cout << ans;
	return 0;
}

B

直接判断交换两个字符之后能不能相等，会有 hack 数据

AC code:

#include <bits/stdc++.h>
using namespace std;

string s, t;

int main(){
	cin >> s >> t;
	if (s == t) return cout << "Yes", 0; 
	for (int i = 0; i < s.size() - 1; i++){
		swap(s[i], s[i + 1]);
		if (s == t) return cout << "Yes", 0;
		swap(s[i], s[i + 1]);
	}
	cout << "No";
	return 0;
}

C

只需要状压一下第一个数选那几个数，然后贪心从大到小 sort 一遍，最后记录最大值

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, len, ans;
int a[15];
vector<int> v1, v2;

int main(){
    cin >> n;
    while (n) a[++len] = n % 10, n /= 10;
    for (int i = 1; i < (1 << len); i++){
        v1.clear(), v2.clear();
        for (int j = 1; j <= len; j++){
            if (i & (1 << (j - 1))) v1.push_back(a[j]);
            else v2.push_back(a[j]);
        }
        sort(v1.begin(), v1.end(), greater<int>());
        sort(v2.begin(), v2.end(), greater<int>());
        int a = 0, b = 0;
        for (int j = 0; j < v1.size(); j++) a = a * 10 + v1[j];
        for (int j = 0; j < v2.size(); j++) b = b * 10 + v2[j];
        ans = max(ans, a * b);
    }
    cout << ans;
    return 0;
}

D

差点没想出来，其实就是差分。

这题跟其他差分题目有一点不一样——他是要记录差分值所对应的下标之和。首先按照正常差分拿个 map 记录哪一位要修改（这里不会 MLE，最多打 \(n\) 个标记）。然后遍历一遍 \(mp\)，因为只有每一个 \(it\) 遍历到的数有操作的，所以只需要记录一个 \(now\) 表示当前值，\(pre\) 表示前一个操作的下标，贡献就是当前下标减去前一个的下标。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, now, pre;
int ans[200005];
map<int, int> mp;

int main(){
	cin >> n;
	for (int i = 1, a, b; i <= n; i++){
		cin >> a >> b; b = a + b - 1;
		mp[a]++, mp[b + 1]--;
	}
	for (auto it : mp){
		ans[now] += it.first - pre, now += it.second, pre = it.first;
	}
	for (int i = 1; i <= n; i++) cout << ans[i] << " ";
	return 0;
}

E

有点像 dp，但不多。

肯定第 \(i\) 个数的贡献就是 \(\sum_{j=1}^{i-1}2^{i-j-1}\) 其中 \(a_j \le a_i\)。根据同底数幂的除法，实际上后面那个幂就是 \(2^{i-1}/2^{j}\)，总和也就是 \(\sum_{j=1}^{i-1} 2^{i-1} \times 2^{-j}\)。提取公因数一下，我们发现其实就是要求 \(\sum_{j=1}^{i-1} 2^{-j}\)，这样就转化成了处理一下符合条件的 \(2^{j-1}\) 的和。

考虑离散化+树状数组，用离散化给这些数字标个顺序，然后按公式求和。因为有离散化，我们把 \(b_i\) 表示 \(a_i\) 离散化之后的位置，所以查询的时候直接查询 \(b_i\) 而不是查询 \(a_i\)，这就保证了查询时第 \(b_i\) 个数前面的数都是比它小的，满足条件；而更新的时候有树状数组的性质肯定保证只会更新比 \(b_i\) 大的数，也就是剩下部分的权值和。

可以 moyou 一下。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, ans;
int a[300005], b[300005], c[1000005];

int ksm(int a, int b){
    int res = 1;
    while (b){
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int lowbit(int x){
    return x & (-x);
}

int query(int x){
    int res = 0;
    while (x){
        res = (res + c[x]) % mod;
        x -= lowbit(x);
    }
    return res;
}

int update(int x, int k){
    int res = 0;
    while (x <= n){
        c[x] += k;
        x += lowbit(x);
    }
    return res;
}

signed main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
    sort(b + 1, b + n + 1);
    int m = unique(b + 1, b + n + 1) - b - 1;
    for (int i = 1; i <= n; i++) a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;//离散化
    for (int i = 1; i <= n; i++){
        ans = (ans + ksm(2, i - 1) * query(a[i]) % mod) % mod;//求之前的总和+提取公因式
        update(a[i], ksm(ksm(2, mod - 2), i));//往后更新a[i]之后的和
    }
    cout << ans;
    return 0;
}

F

前置知识：树的直径。

按照题意，可以先找到这条直径和中心，这里的直径长度指的是经过点数量（包括开头结尾）记为 \(d\)，而这个中心可能是在一条边上或者点上，所以要按直径分奇偶讨论。对于中心节点唯一并且奇偶性位置的证明可以分类讨论一下，或者 moyou。

• 偶数，中心在边上：只用计算这条边连着的两个节点符合要求的数量然后乘相乘，这里符合要求指的是到中心（左边或右边的节点）距离为 \(\frac{d}{2}-1\) 的点。

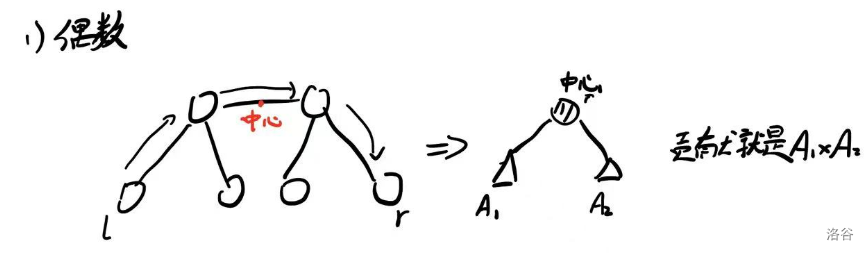
• 奇数，中心在点上：符合要求的点到中心的距离为 \(\lfloor\frac{d}{2}\rfloor\)，那么只需要找每棵子树上到根节点为 \(\lfloor \frac{d}{2}\rfloor\) 的数量，然后组合一下。具体的，设一棵子树符合要求的节点数量为 \(cnt\)，那么贡献就是乘上 \(cnt+1\)，也就是取 \(0\) 个到取 \(cnt\) 个。统计答案把它们乘起来后还要特判一下，减去全部子树都取 \(0\) 个，和只有一个节点的情况。也就是减去 \(\sum cnt+1\)。

  

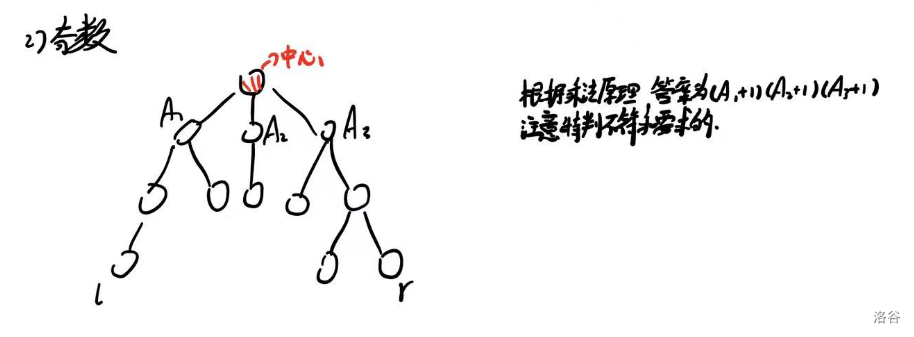
不开 long long 见祖宗。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, maxd, l, r, tmp, cnt, ans = 1;
int fa[200005];
vector<int> g[200005];

void dfs(int x, int f, int st){//找直径
    fa[x] = f;
    if (st > maxd) maxd = st, tmp = x;
    for (int i = 0; i < g[x].size(); i++){
        int v = g[x][i];
        if (v == f) continue;
        dfs(v, x, st + 1);
    }
}

void dfs1(int x, int f, int st){//计算 cnt
    if (st == tmp) cnt++;
    for (int i = 0; i < g[x].size(); i++){
        int v = g[x][i];
        if (v == f) continue;
        dfs1(v, x, st + 1);
    }
}

int main(){
    cin >> n;
    for (int i = 1, u, v; i < n; i++){
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1, 0, 1);//跑两边 dfs 找树的直径
    l = tmp, tmp = maxd = 0;
    dfs(l, 0, 1);//跑完这次 dfs maxd 就已经是直径长度了
    r = tmp;
    if (maxd % 2){//分奇偶讨论
        int x = r;
        for (int i = 1; i <= maxd / 2; i++) x = fa[x];//还原中心
        tmp = maxd / 2;//这里可以模拟一下理解
        for (int i = 0; i < g[x].size(); i++, cnt = 0){
            dfs1(g[x][i], x, 1);//求这一个子树下有多少个节点满足要求
            ans = ans * (cnt + 1) % mod;//乘法原理
        }
        dfs1(x, 0, 0);//处理 cnt 的和
        ans -= cnt + 1;//特判掉不可能的情况
    }
    else{
        int x = r;
        for (int i = 1; i <= maxd / 2 - 1; i++) x = fa[x];//还原中心（左边或右边的节点）
        tmp = maxd / 2 - 1, cnt = 0;
        dfs1(x, fa[x], 0);//这里 fa[x] 就是这条边上的另一个点
        ans = ans * cnt % mod, cnt = 0;//计算贡献
        dfs1(fa[x], x, 0);
        ans = ans * cnt % mod;
    }
    cout << ans;
    return 0;
}

G

有个套路？那就是把坐标系顺时针旋转 \(45 \degree\)，那就要更新一下旋转后的终点坐标和操作。

操作看起来比较容易，画一张坐标系可以发现，新坐标系上的单位长度是旧坐标系上的 \(\sqrt 2\) 倍，而且对应操作也变成了在横坐标和纵坐标上一起移动的形式。我们为了方便操作（解释）就把这个单位长度除以 \(\sqrt 2\)。终点坐标的变换见下图：

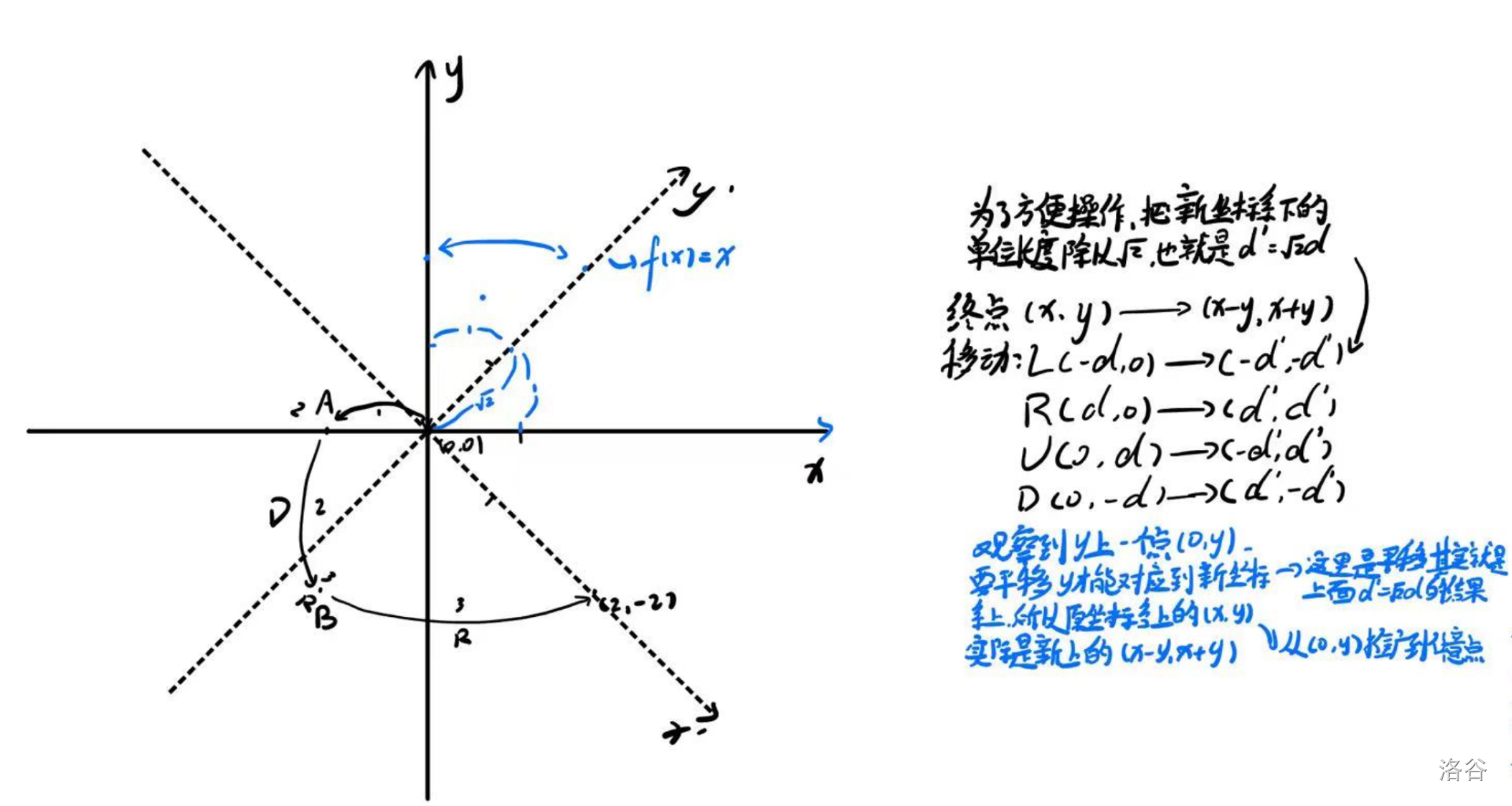
这里需要注意到一点，每次操作横坐标和纵坐标的值更改时相同的，也就是说我们只需要处理一遍 dp 就能处理出来他们俩的可行性。

到了这一步我们的问题就转换成了能否通过 \(\sum_{i=1}^{n}d_i \times a\) 这些移动使得最终坐标为 \((x-y,x+y)\)， 其中 \(a \in \{ -1,1\}\)。有点像背包 dp，但是 \(x\) 不是选和不选的关系，那我们得进一步转换一下：我们先看横坐标（以下都只考虑横坐标，纵坐标类似），将左右两边同时加上 \(\sum d\)，这样左边就成为了 \(\sum_{i=1}^{n}d_i \times (a+1)\)，这里 \(a+1 \in\{0, 2\}\)，右边变成了 \(x-y +\sum d\)。这就有点类似了，但是可以进一步转换一下，左右两边同时除以 \(2\)，这样 \(a+1\) 的值就变成了 \(0\) 或 \(1\)，就转化成可行性 dp 了。

对于 dp，先将 \(x\) 转化成要 dp 的答案，即 \(\frac{x-y+\sum d}{2}\)，设 \(dp_{i,j}\) 表示取前 \(i\) 个状态，能否取到 \(j\) 这个坐标，basecase 为 \(dp_{0,0}=1\)，ans 为 \(dp_{n,x}\)。转移就是 \(dp_{i,j}=dp_{i-1,j}|dp_{i-1,j-d_i}\)。但是这里开数组时间有点炸，需要用 bitset 进行优化，转移方程大致相同，只不过省去了枚举 \(j\) 的循环，直接整体按位或。

判断完不可达之后就是回溯路径的时候了。我们看一下什么时候要取 \(d_i\)，只有当这一位到不了最终答案地时候才肯定要取它，也就是 \(dp_{i,x}=0\) 时就要取。那怎么判断方向呢，我们回到上面提到的在新坐标系中的操作方式（以下横纵坐标都只新坐标系中的），U 和 R 都是有纵坐标的变化的，L 都是 D 有横坐标变化的，那我们就要构造一种记录方式，考虑三进制——每一个数都有唯一的三进制值，仿照这个，设横坐标取的时候权值加 \(1\)，纵坐标加 \(2\)，模拟一下发现每一个方向都有一个唯一的值，这样就可以确定了。

至此完结撒花！！！

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, a, b, x, y, sum;
int d[2005], pos[2005];
bitset<3600005> dp[2005];//数据范围是3.6e6……

int main(){
    cin >> n >> a >> b;
    x = a - b, y = a + b;//更新旋转后终点位置
    for (int i = 1; i <= n; i++) cin >> d[i], sum += d[i];
    if (abs(x) > sum || abs(y) > sum) return cout << "No", 0;//特判
    if ((x + sum) & 1 || (y + sum) & 1) return cout << "No", 0;
    x = (x + sum) / 2, y = (y + sum) / 2;//直接转化成我们dp要去做的东西
    dp[1][0] = 1;//basecase 这里为了之后找路径方便计算（美观）把basecase第一维加了1，后面同理
    for (int i = 1; i <= n; i++) dp[i + 1] = dp[i] | (dp[i] << d[i]);//转移
    if (dp[n + 1][x] == 0 || dp[n + 1][y] == 0) return cout << "No", 0;//特判不可能到达
    for (int i = n; i >= 1; i--){
        int tmp = 0;
        if (!dp[i][x]) x -= d[i], tmp++;//统计方法
        if (!dp[i][y]) y -= d[i], tmp += 2;
        pos[i] = tmp;
    }
    cout << "Yes\n";
    for (int i = 1; i <= n; i++){
        if (pos[i] == 0) cout << "L";//按统计方法输出
        if (pos[i] == 1) cout << "D";
        if (pos[i] == 2) cout << "U";
        if (pos[i] == 3) cout << "R";
    }
    return 0;
}

AT_abc223 复盘

A

water

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;

int main(){
	cin >> n;
	if (n % 100 == 0 && n != 0) cout << "Yes";
	else cout << "No";
	return 0;
}

B

moyou 一遍，记录最大最小

AC code:

#include <bits/stdc++.h>
using namespace std;

string s, mins, maxs;

int main(){
	cin >> s;
	for (int i = 0; i <= s.size(); i++) mins += 'z';
	for (int i = 0; i < s.size(); i++){
		string tmp = s.substr(1) + s[0];
		mins = min(mins, tmp), maxs = max(maxs, tmp);
		s = tmp;
	}
	cout << mins << "\n" << maxs;
	return 0;
}

C

数学，只需要记录一下从前往后和从后往前的到达时间，枚举在哪一段相遇了，最后行程问题一除，再加上前面的路程就好了

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
double a[100005], b[100005], l[100005], r[100005], s[100005];

int main(){
	cin >> n;
	for (int i = 1; i <= n; i++){
		cin >> a[i] >> b[i];
		r[i] = r[i - 1] + a[i] / b[i];
		s[i] = s[i - 1] + a[i];
	}
	for (int i = n - 1; i >= 0; i--) l[i] = l[i + 1] + a[i + 1] / b[i + 1];
	for (int i = 1; i <= n; i++){
		if (l[i] < r[i]){
			double tmp = abs(r[i - 1] - l[i]);
			if (r[i - 1] < l[i]) a[i] = (tmp * b[i] + (a[i] - tmp * b[i]) / 2);
			else a[i] -= tmp * b[i], a[i] /= 2;
//			cout << tmp << endl;
			return printf("%.9lf", s[i - 1] + a[i]), 0;
		}
	}
	return 0;
}

D

不难想到可以建一条单向边来确定遍历的顺序，用拓扑排序来确定这个顺序（没有入度的点一定是满足条件的点）。

题目又要求了要字典序最小，所以可以再拓扑排序的队列改成优先队列，剩下的不变。

AC code:

// LUOGU_RID: 152805703
#include <bits/stdc++.h>
using namespace std;
#define index aaaaaaa
int n, m;
int index[200005], vis[200005];
vector<int> g[200005], ans;
map<pair<int, int>, int> mp;

void bfs(){
	priority_queue<int, vector<int>, greater<int>> q;
	for (int i = 1; i <= n; i++){
		if (index[i] == 0) q.push(i), vis[i] = 1;
	}
	while (!q.empty()){
		int u = q.top(); q.pop();
		ans.push_back(u);
		for (int i = 0; i < g[u].size(); i++){
			int v = g[u][i];
			index[v]--;
			if (index[v] == 0) vis[v] = 1, q.push(v);
		}
	}
}

int main(){
	cin >> n >> m;
	for (int i = 1, u, v; i <= m; i++){
		cin >> u >> v;
		if (mp[{u, v}]) continue;
		mp[{u, v}] = 1;
		g[u].push_back(v);
		index[v]++;
	}
	bfs();
	for (int i = 1; i <= n; i++){
		if (vis[i] == 0) return cout << "-1", 0;
	}
	for (int i = 0; i < ans.size(); i++) cout << ans[i] << " ";
	return 0;
}

E

画几张图，不难发现肯定有一个小矩形的边是和大矩形重合的，并且只有一下两种情况：

• 第一种情况，三个矩形同一个方向。一条边就已经确定了，只用判断剩下的三条边长度之和是不是小于矩形的边。注意：这里三个横的和三个竖的是不一样的，可以直接交换 \(x,y\) 偷懒，共有两种情况
• 第二种情况，两个矩形同一个方向。先摆好不同方向的那个，不难发现下面两个同方向的矩形公共边的长度是确定的，那就判断一下另外两条边之和是不是小于矩形的对应边。这里三个小矩形都可以做方向不同的那个，也就是要分类讨论三次，加上交换 \(x,y\) 的情况，总共六种情况。

按以上思路模拟一遍，最后剩的肯定就是不合法的情况，直接输出 No。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int x, y, a, b, c;

signed main(){
	cin >> x >> y >> a >> b >> c;
	
	int aa = (a + x - 1) / x, bb = (b + x - 1) / x, cc = (c + x - 1) / x;
	if (aa + bb + cc <= y) return cout << "Yes", 0;
	swap(x, y);
	
	aa = (a + x - 1) / x, bb = (b + x - 1) / x, cc = (c + x - 1) / x;
	if (aa + bb + cc <= y) return cout << "Yes", 0;
	swap(x, y);
	
	aa = (a + x - 1) / x;
	if (y - aa > 0){
		bb = (b + y - aa - 1) / (y - aa), cc = (c + y - aa - 1) / (y - aa);
		if (bb + cc <= x) return cout << "Yes", 0;
	}
	bb = (b + x - 1) / x;
	if (y - bb > 0){
		aa = (a + y - bb - 1) / (y - bb), cc = (c + y - bb - 1) / (y - bb);
		if (aa + cc <= x) return cout << "Yes", 0;
	}
	cc = (c + x - 1) / x;
	if (y - cc > 0){
		bb = (b + y - cc - 1) / (y - cc), aa = (a + y - cc - 1) / (y - cc);
		if (aa + bb <= x) return cout << "Yes", 0;	
	}
	swap(x, y);
	
	aa = (a + x - 1) / x;
	if (y - aa > 0){
		bb = (b + y - aa - 1) / (y - aa), cc = (c + y - aa - 1) / (y - aa);
		if (bb + cc <= x) return cout << "Yes", 0;
	}
	bb = (b + x - 1) / x;
	if (y - bb > 0){
		aa = (a + y - bb - 1) / (y - bb), cc = (c + y - bb - 1) / (y - bb);
		if (aa + cc <= x) return cout << "Yes", 0;
	}
	cc = (c + x - 1) / x;
	if (y - cc > 0){
		bb = (b + y - cc - 1) / (y - cc), aa = (a + y - cc - 1) / (y - cc);
		if (aa + bb <= x) return cout << "Yes", 0;	
	}
	
	cout << "No";
	return 0;
}

F

根据某 CF dalao 的想法，可以把左括号的权值设为 \(1\)，右括号为 \(-1\)，那么一个括号串合法就等价于这个串的权值和为 \(0\) 并且任意一个前缀和都大于等于 \(0\)。

具体的，设字符串的左端点为 \(l\)，右端点为 \(r\)，那么有 \(s_r -s_{l-1}=0\) 并且 \(s_k-s_{l-1}\ge 0\)，这里 \(k\in[l,r]\)。稍微地转换一下第二个条件，变成 \(s_k \ge s_{l-1}\)，也就是所有 \(k\in[l,r]\) 都要满足这个条件，也就是 \(\min_{l}^{r}s_k\ge s_{l-1}\)，这就转化成了维护区间最小值。

到这里考虑不带修的情况，直接用前缀和 + ST 表解决，如果带修考虑构建一棵线段树，维护区间和和区间最小值。

先来考虑维护区间和，设交换 \(l\) 和 \(r\)，字符串为 \(str\)，分三种情况讨论：

• \(str_l=str_r\)，不用操作，跳过。
• \(str_l\) 为 (，\(str_r\) 为 )，交换过来就是 \(l\) 之后的前缀和都减少了 \(2\)，\(r\) 之后的前缀和增加了 \(2\)，也就是 \([l,r]\) 的前缀和减少了原来左括号的贡献。
• \(str_l\) 为 )，\(str_r\) 为 (，和第二点类似，只不过是加上了原来右括号的贡献。

现在考虑区间最小值。这个区间最小值不像一般的 lazytag，这个可以用它的子节点进行维护，也就是每次操作之后再去更新这个 tag，直接当作 \(val\) 维护就好。

这里有个偷懒的地方，单点查询的前缀和其实就等效于那一个节点的最小值，不需要再去额外维护。

#include <bits/stdc++.h>
using namespace std;

int n, q;
int s[400005];
string str;
struct tree{
    int l, r, val, add;
}tr[800005];

void pushup(int x){
    tr[x].val = min(tr[x * 2].val, tr[x * 2 + 1].val);
}

void build(int x, int l, int r){
    tr[x].l = l, tr[x].r = r;
    if (l == r) tr[x].val = s[l];
    else{
        int mid = (l + r) >> 1;
        build(x * 2, l, mid);
        build(x * 2 + 1, mid + 1, r);
        pushup(x);
    }
}

void pushdown(int x){
    if (tr[x].add == 0) return ;
    tr[x * 2].add += tr[x].add;
    tr[x * 2 + 1].add += tr[x].add;
    tr[x * 2].val += tr[x].add;
    tr[x * 2 + 1].val += tr[x].add;
    tr[x].add = 0;
}

void update(int x, int l, int r, int k){
    if (tr[x].l >= l && tr[x].r <= r) tr[x].val += k, tr[x].add += k;
    else{
        pushdown(x);
        int mid = (tr[x].l + tr[x].r) >> 1;
        if (l <= mid) update(x * 2, l, r, k);
        if (r > mid) update(x * 2 + 1, l, r, k);
        pushup(x);
    }
}

int query(int x, int l, int r){
    if (tr[x].l >= l && tr[x].r <= r) return tr[x].val;
    pushdown(x);
    int mid = (tr[x].l + tr[x].r) >> 1, res = 2e9;
    if (l <= mid) res = min(res, query(x * 2, l, r));
    if (r > mid) res = min(res, query(x * 2 + 1, l, r));
    return res;
}

int main(){
    cin >> n >> q >> str;
    str = ' ' + str;
    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + (str[i] == '(' ? 1 : -1);
    build(1, 1, n);
    for (int _ = 1, opt, l, r; _ <= q; _++){
        cin >> opt >> l >> r;
        if (opt == 1){
            if (str[l] != str[r]){
                if (str[l] == '(' && str[r] == ')') update(1, l, n, -2), update(1, r, n, 2);
                else update(1, l, n, 2), update(1, r, n, -2);
                swap(str[l], str[r]);
            }
        }
        else{
            int tmp1 = (l == 1 ? 0 : query(1, l - 1, l - 1));
            int tmp2 = query(1, r, r); 
            if (tmp1 != tmp2) cout << "No\n";
            else if (query(1, l, r) >= tmp1) cout << "Yes\n";
            else cout << "No\n";
        }
    }
	return 0;
}

G

树的二分图最大匹配 = 总结点数 - 最大独立集。

显然需要先去计算原树上的最大独立集是多少。考虑 dp，设 \(f_{u,0/1}\) 表示取或不取 \(u\) 时 \(u\) 的子树上最大独立集的大小，转移有两种：

• \(f_{u,0}=\sum \max(f_{v,0},f_{v,1})\)，其中 \(v\) 是 \(u\) 的子节点。
• \(f_{u,1}=\sum f_{v,0} + 1\)，其中 \(v\) 是 \(u\) 的子节点。

这里 \(f\) 是从叶子节点往上转移的，\(f_V\) 都已经求得。求出来这些之后，原树的最大独立集就是 \(\max (f_{1,0},f_{1, 1})\)，匹配数为 \(n-\max(f_{1,0},f_{1,1})\)。记得初始化每一个点 \(f_{u,1} = 1\)。

之后的问题就变成了如何计算删去一个节点的贡献，可以继续用换根 dp。有了上面的 \(f\)，这一步就很方便了，删去这个节点出来的答案就是这个节点上面的加上子树上的。我们就需要另一个数组 \(g\) 来记录 \(u\) 上面的最大独立集个数，按照 \(f\) 的方法，\(g_{u,0/1}\) 表示取或不取 \(fa_u\) 时，\(u\) 子树之外的最大独立集大小，还是分两种转移：

• \(g_{u,0}=\max(g_{fa,0},g_{fa,1})+f_{fa,0}-\max(f_{u,0},f_{u,1})\)。
• \(g_{u,1}=g_{fa,0}+f_{fa,1}-f_{u,0}\)。

这里 \(g\) 是从根节点往下转移的，所以 \(g_{fa}\) 的值是知道的。这时不选 \(u\) 的最大独立集是 \(f_{u,0}+\max(g_{u,0},g_{u,1})\)，匹配数为 \(n-1-(f_{u,0}+\max (g_{u,0},g_{u,1}))\)，与原树的匹配数比较一下，统计答案。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, ans;
int f[200005][2], g[200005][2];
vector<int> e[200005];

void dfs1(int x, int fa){
    f[x][1] = 1;//初始化
    for (int i = 0; i < e[x].size(); i++){
        int v = e[x][i];
        if (v == fa) continue;
        dfs1(v, x);//先往下递归，再向上转移
        f[x][0] += max(f[v][0], f[v][1]);//转移
        f[x][1] += f[v][0];
    }
}

void dfs2(int x, int fa){
    for (int i = 0; i < e[x].size(); i++){
        int v = e[x][i];
        if (v == fa) continue;
        g[v][0] = max(g[x][0], g[x][1]) + f[x][0] - max(f[v][0], f[v][1]);//先向下转移，再往下递归
        g[v][1] = g[x][0] + f[x][1] - f[v][0];//转移
        dfs2(v, x);
    }
}

int main(){
    cin >> n;
    for (int i = 1, u, v; i < n; i++){
        cin >> u >> v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    dfs1(1, 0);
    dfs2(1, 0);
    for (int i = 1; i <= n; i++){
        if (n - 1 - (f[i][0] + max(g[i][0], g[i][1])) == n - max(f[1][1], f[1][0])) ans++;//判断两个匹配是否相等
    }
    cout << ans;
    return 0;
}

AT_abc229 复盘

A

if 判断不可能情况

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

string s[2];

signed main(){
	cin >> s[0] >> s[1];
	if ((s[0][0] == '#' && s[1][1] == '#' && s[0][1] == '.' && s[1][0] == '.') || (s[1][0] == '#' && s[0][1] == '#' && s[0][0] == '.' && s[1][1] == '.')) cout << "No";
	else cout << "Yes";
	return 0;
}

B

moyou

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int a, b;

signed main(){
	cin >> a >> b;
	while (a && b){
		if (a % 10 + b % 10 >= 10) return cout << "Hard", 0;
		a /= 10, b /= 10;
	}
	cout << "Easy";
	return 0;
}

C

贪心

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, w, ans;
struct node{
	int a, b;
}t[300005];

bool cmp(node x, node y){
	return x.a > y.a;
}

signed main(){
	cin >> n >> w;
	for (int i = 1; i <= n; i++) cin >> t[i].a >> t[i].b;
	sort(t + 1, t + n + 1, cmp);
	for (int i = 1; i <= n; i++){
		if (t[i].b > w){
			ans += t[i].a * w;
			break;
		}
		ans += t[i].a * t[i].b;
		w -= t[i].b;
	}
	cout << ans;
	return 0;
}

D

只需要把 . 看作 \(1\)，X 看作 \(0\)，然后维护一个前缀和，双指针一下就好了

AC code:

#include <bits/stdc++.h>
using namespace std;

int k, ans;
int a[200005];
string s;

int main(){
	cin >> s >> k;
	for (int i = 0; i < s.size(); i++) a[i + 1] = a[i] + (s[i] == '.');
	for (int l = 1, r; r <= s.size(); r++){
		while (a[r] - a[l - 1] > k && l <= r) l++;
		ans = max(ans, r - l + 1);
	}
	cout << ans;
	return 0;
}

E

一眼倒着来操作，加上每一个点和这个点的对应边，加上点并查集的板子，记录个 \(ans\) 最后倒序输出。

细节比较多，\(ans\) 的统计是在操作之前；操作的时候分类讨论一下：

• 加入的点没有出现过，\(cnt+1\)。
• 加入的点出现过，并且不在同一个连通块中，\(cnt-1\) 并且合并连通块。

还需要特判一下加入的点是否是小于 \(u\) 的，如果是直接跳过（不影响答案，后面还会再统计回来）。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, m, cnt;
int fa[200005], vis[200005], ans[200005];
vector<int> g[200005];

int find(int x){//banzi
	return x == fa[x] ? x : fa[x] = find(fa[x]);
}

signed main(){
	cin >> n >> m;
	for (int i = 1; i <= n; i++) fa[i] = i;
	for (int i = 1, u, v; i <= m; i++){
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for (int u = n; u >= 1; u--){
		ans[u] = cnt;//记录答案
		cnt++;
		vis[u] = 1;
		for (int i = 0; i < g[u].size(); i++){
			int v = g[u][i];
			if (v < u) continue;//下次一定
			if (vis[v] == 0) cnt++, vis[v] = 1;//特判
			if (find(u) != find(v)){
				cnt--;
				fa[find(u)] = find(v);
			}
		}
	}
	for (int i = 1; i <= n; i++) cout << ans[i] << endl;
	return 0;
}

F

一眼若只 dp。

根据二分图的判定方法，有染色法：按照 dfs 相间染色，如果最后能够合法地染完，即没有一个点既是 \(1\) 又是 \(0\) 处于量子叠加态，那么就是一个二分图。

不妨假设 \(0\) 号节点染的 \(0\)，设 \(dp_{i,j}\) 表示 \(i\) 号节点染成 \(j\) 颜色所删除的边权值最小值，其中 \(j\in\{0,1\}\)。转移分四类讨论，和上一个点颜色的异同 + 和 \(0\) 号点颜色的异同。

但是这样 WA 了，不难发现 \(n\) 号点和 \(1\) 号点的边是默认断开了（没有考虑 \(n\) 的后一个点是 \(1\)）。直接对 dp 加上一维 \(k\) 表示第一个点取什么颜色，basecase 变成 \(dp_{1,1,0}=dp_{1,0,1}=\inf\)，\(dp_{1,0,0}=a_1\)。而转移就真的要分 \(8\) 类了，但是最后一维其实不用考虑怎么转移，只是在最后处理答案的时候多来一步，也就是原来的 \(4\) 类。最后的答案就是 \(n\) 和 \(1\) 要不要删边（这里前面转移到 \(n\) 的时候已经处理过要不要和 \(0\) 删边）。

AC code：

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n;
int a[200005], b[200005], dp[200005][2][2];

signed main(){
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];
	dp[1][1][0] = dp[1][0][1] = 1e18, dp[1][0][0] = a[1];
	for (int i = 2; i <= n; i++){
		dp[i][0][0] = min(dp[i - 1][0][0] + b[i - 1], dp[i - 1][1][0]) + a[i];
		dp[i][0][1] = min(dp[i - 1][0][1] + b[i - 1], dp[i - 1][1][1]) + a[i];
		dp[i][1][0] = min(dp[i - 1][1][0] + b[i - 1], dp[i - 1][0][0]);
		dp[i][1][1] = min(dp[i - 1][1][1] + b[i - 1], dp[i - 1][0][1]);
	}
	cout << min(min(dp[n][0][1], dp[n][1][0]), min(dp[n][0][0], dp[n][1][1]) + b[n]);
	return 0;
}

G

考虑一个很神奇的转化，假设原数组中 Y 的位置为 \(a_i\)，那么可以把 \(b_i\) 设成 \(a_i-i\)。这样在 \(b_i\) 上 \(+1\) 或 \(-1\) 就相当于在原数组中交换了两个数，而最终答案也变成了用 \(k\) 次操作使得最终相等的数最多的数量。

有一个朴素的想法：枚举最终答案，判断答案是否可行，这里的 \(check\) 直接判断是否存在一个区间 \([l,r]\) 使得 \(\sum_{i=l}^{r}|a_x-b_i|\le k\)，这里 \(x\) 是 \([l,r]\) 中的一个数。而这个问题非常典型，最小值肯定是 \(x\) 取 \(\frac{l+r}{2}\) 时，维护一下前缀和就能在 \(O(1)\) 判断 + \(O(n)\) 枚举区间解决。

而这个问题是满足单调性的，可以直接二分，去二分它的最终答案，再 \(check\) 一下判断答案是否可行。总共复杂度 \(O(n\log n)\)。

二分的时候要从 \(0\) 开始，记得改一下取 \(mid\) 的地方，不然会 TLE。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int k, n, cnt;
int a[200005], s[200005];
string str;

bool check(int x){
	for (int i = 1; i <= n - x + 1; i++){//check是否有一个左端点满足条件
		int l = i, r = i + x - 1, mid = l + r >> 1;
		int sum = a[mid] * (mid - l + 1) - (s[mid] - s[l - 1]) + (s[r] - s[mid]) - a[mid] * (r - mid);
		if (sum <= k) return 1;
	}
	return 0;
}

signed main(){
	cin >> str >> k;
	for (int i = 0; i < str.size(); i++){
		if (str[i] == 'Y') a[++n] = i + 1 - n;
	}
	for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];//前缀和
	int l = 0, r = n;
	while (l < r){//二分答案
		int mid = (l + r + 1) >> 1;
		if (check(mid)) l = mid;
		else r = mid - 1;
	}
	cout << l;
	return 0;
}

EX-CF154C

考虑集合哈希，就是判断两个集合是否相同。

这题显然是集合哈希，对每个点附上一个哈希值，然后在连边的时候加上对应顶点的哈希值，最后只要判断有多少个数哈希值相同然后 \(C_{n}^2\) 一下就好。

这里要特判一下两两连边的情况，可以稍微画个图理解一下——两两连边后这两个点的哈希值其实是记录的其他点的权值，但是自己没有记录到，所以要加一下自己的哈希值然后判断是否相同。

这里模数可以选用 \(1145141119\)。

#include <bits/stdc++.h>
#define int unsigned long long
using namespace std;

const int P = 11451411119;
int n, m, cnt, ans;
int a[2000005], b[2000005], hs[2000005], pw[2000005];

signed main(){
	cin >> n >> m;
	pw[0] = 1;
	for (int i = 1; i <= n; i++) pw[i] = pw[i - 1] * P;//自然溢出哈希值
	for (int i = 1; i <= m; i++){
		cin >> a[i] >> b[i];
		hs[a[i]] += pw[b[i]];
		hs[b[i]] += pw[a[i]];
	}
	for (int i = 1; i <= m; i++){
		if (hs[a[i]] + pw[a[i]] == hs[b[i]] + pw[b[i]]) ans++;
	}
	sort(hs + 1, hs + n + 1);
	for (int i = 1; i <= n; i++){
		if (hs[i] == hs[i - 1]) cnt++;
		else ans += cnt * (cnt - 1) / 2, cnt = 1;
	}
	cout << ans + cnt * (cnt - 1) / 2;
	return 0;
}

AT_abc238 复盘

A

挺简单的，简单画个图或者枚举一下

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;

int main(){
	cin >> n;
	if (n >= 2 && n <= 4) cout << "No";
	else cout << "Yes";
	return 0;
}

B

把每个切点丢到数组里或优先队列，然后一个一个出队看最大的块

注意要把 0 和 360 也放进去

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, a, lst, ans;
priority_queue<int> q;

int main(){
	cin >> n;
	q.push(0);
	for (int i = 1; i <= n; i++){
		cin >> a;
		lst = (lst + a) % 360;
		q.push(lst);
	}
	q.push(360);
	while (q.size() > 1){
		int x = q.top(); q.pop();
		int y = q.top();
		ans = max(ans, x - y);
	}
	cout << ans;
	return 0;
}

C

简简单单一个公式，稍微在草稿纸上推一下每一位的公式

but 在写完之后公式错了。。。加上有一个地方没有模调了 1h。。。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, ans;

signed main(){
	cin >> n;
	int lst = 0;
	for (; pow(10, lst + 1) <= n; lst++){
		ans = (ans + (1 + (int)pow(10, lst + 1) - (int)pow(10, lst)) % mod * (((int)pow(10, lst + 1) - (int)pow(10, lst)) % mod) / 2) % mod;
	}
	ans = (ans + (1 + n - (int)pow(10, lst) + 1) % mod * ((n - (int)pow(10, lst) + 1) % mod) / 2) % mod;
	cout << ans;
	return 0;
}

D

D 有点抽象，但不多

首先考虑结论，容易得到如果 \(a \ge s\) 时肯定不行

之后举几个例子发现 \(s\) 减去了 \(x,y\) 中的两个 \(a\) 之后剩下的数合法情况与 \(a\) 是为 \(0\) 的，而且这个剩下的数大于 \(0\)。

很简单，如果剩下的数那几位还是 \(1\)，就说明 \(x\) 和 \(y\) 中有一位是 \(1\) (不可能是进位上来的，前面都是最多一位为 \(1\))，那么加上 \(a\) 再与会发现这一位与出来是 \(0\)。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int t, a, b;

signed main(){
    cin >> t;
    while (t--){
        cin >> a >> b;
        int s = b - 2 * a;
        if (s < 0 || (s & a) != 0) cout << "No\n";
        else cout << "Yes\n";
    }
    return 0;
}

E

很难想到可以用并查集。

在输入每一个数据的时候建一条 \((u-1,v)\) 的边，并放入并查集。最后判断 \(0\) 和 \(n\) 是否联通。

非常神奇，模拟一下发现这就等同于要求有好几个区间连续拼成一整个区间。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, q;
int fa[200005];

int find(int x){
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

void merge(int x, int y){
    fa[find(y)] = find(x);
}

signed main(){
    cin >> n >> q;
    for (int i = 1; i <= n; i++) fa[i] = i;
    for (int i = 1, u, v; i <= q; i++){
        cin >> u >> v;
        merge(u - 1, v);
    }
    cout << ((find(0) == find(n)) ? "Yes" : "No");
    return 0;
}

F

贪心+dp

先按 \(a\) 排一边序，定义 \(dp_{i,j,k}\) 表示前 \(i\) 位取了 \(j\) 位未选最小值为 \(k\)。

考虑转移，我们发现枚举到 \(i\) 时通过 \(i-1\) 转移不好转，考虑从 \(i\) 转到 \(i + 1\)。

分两种情况讨论：

• 取这个数，因为 \(a_i\) 肯定大于前面的，只能是 \(b_i < k\) 才能转，\(dp_{i + 1,j + 1,k}+=dp_{i,j,k}\)。
• 不取这个数，那么就要转移到 \(min(k,b_i)\) 上，\(dp_{i+1,j,\min{b_i},k}+=dp_{i,j,k}\)。

最后答案就是 \(\sum_{i=1}^{n+1}{dp_{n,m,i}}\)，这里 \(n\) 可能等于 \(k\)，所以要枚举到 \(n+1\)。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, m, ans;
int dp[305][305][305];
struct node{
    int p, q;
}a[305];

bool cmp(node x, node y){
    return x.p < y.p;
}

signed main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i].p;
    for (int i = 1; i <= n; i++) cin >> a[i].q;
    sort(a + 1, a + n + 1, cmp);
    dp[0][0][n + 1] = 1;
    for (int i = 0; i < n; i++){
        for (int j = 0; j <= m; j++){
            for (int k = 1; k <= n + 1; k++){
                if (a[i + 1].q < k && j != m) dp[i + 1][j + 1][k] = (dp[i + 1][j + 1][k] + dp[i][j][k]) % mod;
                dp[i + 1][j][min(k, a[i + 1].q)] = (dp[i + 1][j][min(k, a[i + 1].q)] + dp[i][j][k]) % mod;
            }
        }
    }
    for (int i = 1; i <= n + 1; i++) ans = (ans + dp[n][m][i]) % mod;
    cout << ans;
    return 0;
}

AT_abc240 复盘

A

if

AC code:

#include <bits/stdc++.h>
using namespace std;

int a, b;

int main(){
    cin >> a >> b;
    if (a + 1 == b || b + 1 == a) cout << "Yes";
    else if ((a == 1 && b == 10) || (a == 10 && b == 1)) cout << "Yes";
    else cout << "No";
    return 0;
}

B

map

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
int a[200005];
map<int, int> mp;

int main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], mp[a[i]] = 1;
    cout << mp.size();
    return 0;
}

C

简单 dp，设置状态 \(dp_{i,j}\) 表示取前 \(i\) 个能不能取到 \(j\)，转移就是 \(dp_{i,j} = \max(dp_{i,j},dp_{i-1,j-a_i/j-b_i})\)，这里 \(\max\) 就相当于判断是否可以到达。或者使用 bitset

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, x;
int a[105], b[105], dp[105][10005];

signed main(){
    cin >> n >> x;
    for (int i = 1; i <= n; i++) cin >> a[i] >> b[i];
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++){
        for (int j = 0; j <= x; j++){
            if (j - a[i] >= 0) dp[i][j] |= dp[i - 1][j - a[i]];
            if (j - b[i] >= 0) dp[i][j] |= dp[i - 1][j - b[i]];
        }
    }
    if (dp[n][x] == 1) cout << "Yes";
    else cout << "No";
    return 0;
}

D

考虑栈，按照题目要求操作，把每一个相同数字的集合存下来，记录一坨数的数字和数量，然后用一个 \(l\) 和 \(r\) 维护左边的连通块号和右边的，再记录一个最后块号。

加入的时候判断 \(a_i\) 是否与上一个连通块的数字相同，如果不相同就新开一个，更新一下 \(l,r,ed\)。删除操作只需要判断最后一个连通块中的数量是否等于 \(a_i\)，如果是就删除这些元素然后更新 \(ed\)。答案就是 \(st.size\)。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, cnt, ed;
int a[200005], l[200005], r[200005];
pair<int, int> len[200005];
stack<int> st;

signed main(){
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++){
        if (a[i] == len[ed].first) len[ed].second++;
        else{
            len[++cnt] = {a[i], 1};
            r[ed] = cnt, l[cnt] = ed, ed = cnt;
        }
        st.push(a[i]);
        if (len[ed].second == a[i]){
            while (len[ed].second) st.pop(), len[ed].second--;
            ed = l[ed];
        }
        cout << st.size() << endl;
    }
    return 0;
}

E

类似线段树，可以把叶子节点设成 \(l=r\)，注意每一个叶子节点的 \([l,r]\) 要不一样。之后直接转移，当前节点的 \(l\) 就是子节点的 \(l\) 的最小值，\(r\) 就是子节点的最大值，慢慢网上转移。

注意：在判断叶子节点的时候要特判一下不是根节点。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, cnt;
int l[200005], r[200005];
vector<int> g[200005];

void dfs(int x, int fa){
    if (x != 1 && g[x].size() == 1) l[x] = r[x] = ++cnt;
    for (int i = 0; i < g[x].size(); i++){
        int v = g[x][i];
        if (v == fa) continue;
        dfs(v, x);
        l[x] = min(l[x], l[v]), r[x] = max(r[x], r[v]);
    }
}

int main(){
    cin >> n;
    memset(l, 0x3f, sizeof(l));
    for (int i = 1, u, v; i < n; i++){
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1, 1145141);
    for (int i = 1; i <= n; i++) cout << l[i] << " " << r[i] << endl;
    return 0;
}

F

比较简单的一题，可以先把样例模拟一遍，设 \(s1_i\) 表示第 \(i\) 串数字末尾在 \(B\) 中的值，不难看出 \(s1_i\) 是由 \(x_iy_i\) 构成的；设 \(s_i\) 表示第 \(i\) 串数字末尾在 \(A\) 中的值，也就是 \(B\) 中这前 \(i\) 串数字的前缀和。不难看出 \(x_i\) 对 \(s_i\) 的贡献实际是 \(\sum_{j=1}^{y_i}j \times x_i\)，再加上 \(s1_{i-1}\) 在计算 \(B\) 中这一串数字的前缀和时的贡献 \(s1_{i-1}y_i\)，和原本就有的贡献 \(s_{i-1}\)，最终得到递推式 \(s_i=s_{i-1}+\sum_{j=1}^{y_i}j \times x_i+s1_{i-1}y_i\)。

这就结束了吗？我们发现一串数字的最后一个数不一定是最大的，有可能在中间取到最大值，这就需要特判一下，如果 \(x_i<0\) 就要考虑是否会出现这种情况。对于 \(A\) 是 \(B\) 的前缀和，所以 \(B\) 中值为正的部分都对 \(A\) 有贡献，那么可能的最大值就要加上这一串的贡献。而这一串数肯定也是满足等差数列的，我们就可以直接求出项数，然后计算一下这一串的和，再取个 \(\max\)。

细节：我们再计算项数的时候要和 \(y_i\) 取个 \(\min\)，不能取的项数比这一串数字的长度还多；并且还要和 \(1\) 取个 \(\max\)，避免出现 \(\frac{s1_{i-1}}{-x_i}<0\) 的情况（也是不合法的）。

AC code：

#include <bits/stdc++.h>
#define int long long
using namespace std;

int t, n, m;
int x[200005], y[200005], s[200005], s1[200005];

signed main(){
    cin >> t;
    while (t--){
        cin >> n >> m;
        for (int i = 1; i <= n; i++) cin >> x[i] >> y[i], s1[i] = s1[i - 1] + x[i] * y[i];
        int ans = -1e18;//记得设成-inf
        for (int i = 1; i <= n; i++){
            if (x[i] < 0){//特判中间的情况
                int tmp = max(1ll, min(s1[i - 1] / abs(x[i]), y[i]));
                ans = max(ans, s[i - 1] + (s1[i - 1] + x[i] + s1[i - 1] + tmp * x[i]) * tmp / 2);
            }
            s[i] = s[i - 1] + s1[i - 1] * y[i] + x[i] * y[i] * (y[i] + 1) / 2;//递推式子
            ans = max(ans, s[i]);
        }
        cout << ans << endl;
    }
    return 0;
}

G

类似这题，有个套路，把平面旋转 \(45\degree\)。

这题是三维的，显然不好做，那么可以先枚举第一维，就转化成二维平面中是否能从 \((0,0)\) 走到 \((y,z)\)。

按照这题的思路，直接旋转一下，就变化成了 \((0,0)\) 走到 \((y-z,y+z)\)，每一步也变成了 \((1,-1)\) 或 \((1,1)\) 或 \((-1,-1)\) 或 \((-1,1)\)，可以进行单独操作了，证明过程参考这题的题解。

之后的步骤还可以优化一下，先考虑一个问题，如果走了 \(a\) 步 \(+1\)，\(b\) 步 \(-1\)，总共走了 \(k\) 步，目的地是 \(x\)，可以得到一个方程组：

\[\begin{cases} a-b=x\\ a+b=k \end{cases} \]

简单学过小学数学的就知道，\(a=\frac{x+k}{2},b=\frac{x-k}{2}\)，而最终方案就是 \(C_k^a=C_k^b\)。拓展到这题上面，最终目的地是 \((y-z,y+z)\)，都是走 \(k\) 步，那么最终方案就是到 \(y-z\) 的方案数乘上到 \(y+z\) 的方案数，也就是：

\[C_k^{\frac{k+y-z}{2}} \times C_{k}^\frac{k+y+z}{2} \]

不过这里还需要特判一下能否到达，以及分子部分能不能被 \(2\) 整除。

对于第一维的判断，也是枚举走多少个正的，也可以得到走多少个负的；设走了 \(a\) 步 \(+1\)，\(b\) 步 \(-1\)，那么最终方案数就是 \(C_n^a\times C_{n-a}^b\)，当然 \(a+b\le n\)。

最终答案就是三维的方案数乘起来。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
const int N = 1e7;
int n, x, y, z, ans;
int fac[N + 5], inv[N + 5];

int ksm(int a, int b){
	int res = 1;
	while (b){
		if (b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

int C(int x, int y){
	return fac[x] * inv[x - y] % mod * inv[y] % mod;
}

int solve(int k, int kx, int ky){
	int a = abs(kx - ky), b = abs(kx + ky);
	if (k + a & 1 || k + b & 1 || k < a || k < b) return 0;
	return C(k, k + a >> 1) * C(k, k + b >> 1) % mod;//方程组求解加上组合数
}

signed main(){
	cin >> n >> x >> y >> z;
	x = abs(x), y = abs(y), z = abs(z);
	fac[0] = 1;
	for (int i = 1; i <= N; i++) fac[i] = fac[i - 1] * i % mod;//预处理阶乘
	inv[N] = ksm(fac[N], mod - 2);
	for (int i = N - 1; i >= 0; i--) inv[i] = inv[i + 1] * (i + 1ll) % mod;//预处理逆元
	for (int i = 0, j = x; i + j <= n; i++, j++){//i走负的，j走正的
		ans = (ans + C(n, i) * C(n - i, j) % mod * solve(n - i - j, y, z) % mod) % mod;//乘法原理统计答案
	}
	cout << ans;
	return 0;
}

EX-CF1510D

很容易想到 \(dp\)。

设 \(dp_{i,j}\) 表示前 \(i\) 个数取一些数乘积末尾为 \(j\) 的最大值。转移非常简单，\(dp_{i,(j\times a_i)\bmod 10}=\max(dp_{i,(j\times a_i)\bmod10},dp_{i-1,j} \times a_i)\)。但是这个数会非常大，高精度都救不了，所以要转化一下。

众所周知 \(\lg ab=\lg a+\lg b\)，并且 \(\lg\) 在正数范围内还是单调递增的，也就是说，我们可以把 \(dp_{i,j}\) 的值取个 \(\log\)，然后乘 \(a_i\) 的操作就变成了加 \(\lg a_i\)，最终答案也是正确的。转移就变成了 \(\max(dp_{i-1,j}+\lg a_i)\)。

但是这题还要记录每一步取了什么数，也就是说在转移的时候还要记录是从哪一位、哪一个数转移过来的最大值。考虑维护一个 \(lst_{i,j}\) 表示对应的 \(dp_{i,j}\) 是从哪里转移过来。最后递归一下，如果记录的 \(lst_{i,j}\) 对 \(dp_{i,j}\) 有贡献的话，说明可以从这一位转移过来，就记录一下答案。注意：要特判一下 \(1\) 的情况，如果 \(lst_{i,j}=\{0,0\}\) 就直接 return。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, k, cnt;
int a[100005], ans[100005];
double dp[200005][10];
pair<int, int> lst[100005][10];

void dfs(int x, int y){
	int nx = lst[x][y].first, ny = lst[x][y].second;
	if (dp[x][y] != dp[nx][ny] || a[x] % 10 == 1) ans[++cnt] = a[x];//有贡献就记录
	if (nx == 0 && ny == 0) return ;
	dfs(nx, ny);
}

signed main(){
	cin >> n >> k;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++){
		dp[i][a[i] % 10] = log2(a[i]);
		for (int j = 0; j <= 9; j++){
			if (dp[i - 1][j] && dp[i - 1][j] + log2(a[i]) > dp[i][(j * a[i]) % 10]){//转移+记录路径
				dp[i][(j * a[i]) % 10] = dp[i - 1][j] + log2(a[i]);
				lst[i][(j * a[i]) % 10] = {i - 1, j};
			}
			if (dp[i - 1][j] > dp[i][j]){//注意还要继承一下上一位
				dp[i][j] = dp[i - 1][j];
				lst[i][j] = {i - 1, j};
			}
		}
	}
	if (!dp[n][k]) return cout << "-1", 0;
	dfs(n, k);//采用递归的方式记录答案
	cout << cnt << endl;
	for (int i = 1; i <= cnt; i++) cout << ans[i] << " ";
	return 0;
}

AT_abc243 复盘

A

water

AC code:

#include <bits/stdc++.h>
using namespace std;

int v, a, b, c;

int main(){
	cin >> v >> a >> b >> c;
	v -= v / (a + b + c) * (a + b + c);
	if (v < a) cout << "F";
	else if (v < a + b) cout << "M";
	else if (v < a + b + c) cout << "T";
	return 0;
}

B

直接 moyou

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, cnt1, cnt2;
int a[1005], b[1005];

int main(){
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];
	for (int i = 1; i <= n; i++){
		for (int j = 1; j <= n; j++){
			if (a[i] == b[j]){
				if (i == j) cnt1++;
				else cnt2++;
			}
		}
	}
	cout << cnt1 << "\n" << cnt2;
	return 0;
}

C

赛时脑抽了，只要记录同一行下最右边向左的点和最左边向右的点，判断一下是否有重合部分就好了

AC code:

#include <bits/stdc++.h>
using namespace std;

int n;
int x[200005], y[200005];
string s;
map<int, vector<pair<int, int>>> mp;

int main(){
	cin >> n;
	for (int i = 0; i < n; i++){
		cin >> x[i] >> y[i];
		mp[y[i]].push_back({x[i], i});
	}
	cin >> s;
	for (auto it : mp){
		int posa = 0, posb = 0x3f3f3f3f;
		for (int i = 0; i < it.second.size(); i++){
			if (s[it.second[i].second] == 'L') posa = max(posa, it.second[i].first);
			if (s[it.second[i].second] == 'R') posb = min(posb, it.second[i].first);
		}
		if (posa > posb) return cout << "Yes", 0;
	}	
	cout << "No";
	return 0;
}

D

有思维，但不多。

读题很容易发现 L 和 R 操作是可以和 U 操作抵消掉的（必须是 U 在 L 和 R 的后面），那就可以先按括号匹配的方式处理一遍，接着模拟输出。具体的，遇到 L 或 R 就入；如果是 U 且栈空，那么将 U 加入栈内，否则将栈顶弹出（抵消）。在抵消的时候要判断栈内要抵消的那个元素是不是 U，如果是就不操作。

注意：最终操作序列是上面记录的栈中从栈底到栈顶的序列。

但是为什么这样做不会越界？模拟一遍，我们发现最终操作序列中肯定是一堆 U 后面跟着 L 和 R，先上再下肯定不会炸（题目保证最终答案不会炸）。

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n, x;
string s;
stack<char> st, stk;

signed main(){
	cin >> n >> x >> s;
	for (int i = 0; i < s.size(); i++){
		if (s[i] == 'U'){
			if (!st.empty() && (st.top() == 'L' || st.top() == 'R')) st.pop();
			else st.push(s[i]);
		}
		else st.push(s[i]);
	}
	while (!st.empty()) stk.push(st.top()), st.pop();
	while (!stk.empty()){
		char c = stk.top(); stk.pop();
		if (c == 'U') x /= 2;
		if (c == 'L') x *= 2;
		if (c == 'R') x = x * 2 + 1;
	}
	cout << x;
	return 0;
}

E

我们有了一个朴素的思路：用 dijkstra 跑一遍“全源最短路”记录哪条边没有在任意一条最短路上然后统计答案即可。

但是上面这个方法很难实现，那就去想 Floyd。Floyd 很容易求出来全源最短路，但是哪条边是最短路上的边不知道，现在问题就转换成了：已知任意两个点之间的最短路，求哪条边是在最短路上的。

考虑 Floyd 的性质，经过松弛的边肯定不是最短路，那只要在处理完 \(dis\) 之后枚举所有边，看这条边是否被松驰过，如果是直接累加答案。具体的，松弛操作的判断可以直接去枚举除了这条边两个端点的点 \(k\) 看这两个端点到 \(k\) 的距离是否是他们俩的最短距离就好了。

这里我们不用考虑删完边后它是不是联通的，因为如果有一条边是最短路上的边，它一定没有被松弛，统计答案时也不会记录它，而这条边肯定是它左侧部分点到右侧部分点最短路上的，也就是这条边左边和右边的点至少有这条边连着，肯定是联通的。

最终复杂度 \(O(n^3+nm)\) 可以过。

AC code:

#include <bits/stdc++.h>
using namespace std;

int n, m, ans;
int dis[305][305];//最短路数组
struct edge{
    int u, v, w;
}e[100005];

int main(){
    cin >> n >> m;
    memset(dis, 0x3f, sizeof(dis));
    for (int i = 1, u, v, w; i <= m; i++){
        cin >> u >> v >> w;
        e[i].u = u, e[i].v = v, e[i].w = w;
        dis[u][v] = dis[v][u] = w;
    }
    for (int i = 1; i <= n; i++) dis[i][i] = 0;
    for (int k = 1; k <= n; k++){
        for (int i = 1; i <= n; i++){
            for (int j = 1; j <= n; j++) dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);//Floyd
        }
    }
    for (int i = 1; i <= m; i++){
        int flag = 0;
        for (int j = 1; j <= n; j++){
            if (j != e[i].u && j != e[i].v && dis[e[i].u][e[i].v] == dis[e[i].u][j] + dis[j][e[i].v]) flag = 1;//被松驰过，记录答案
        }
        ans += flag;
    }
    cout << ans;
    return 0;
}

F

前置知识《伯努利试验》：设一个事件 \(A\) 发生的概率 \(P(A)\)，则取 \(p\) 次这个事件，恰好有 \(k\) 次发生的概率是 \(C_{p}^{k} \times {P(A)}^k \times {(1-P(A))}^{p-k}\)。在这里就表现为 dp 和组合计数。

依旧是 dp，设置状态 \(dp_{i,j,k}\) 表示前 \(i\) 种角色，抽了 \(j\) 次，有 \(k\) 种不同角色的概率。

类似《伯努利试验》，设在前 \(j\) 次抽卡中抽到了 \(p\) 个角色 \(i\)，所以它的贡献就是 \(C_{j}^{p} \times {(\frac{w_i}{\sum w})}^p \times dp_{i-1,j-p,k-1}\)，这里乘上的 \(dp_{i-1,j-p,k-1}\) 已经代表剩下的数全抽 \(i\) 以前的角色的概率，不用再乘上 \({(1-P(A))}^{p-k}\)。\(dp_{i,j,k}\) 的答案就是这些贡献求和。这里转移前记得先将 \(dp_{i,j,k}\) 赋值成 \(dp_{i-1,j,k}\)。

basecase 就是 \(dp_{0,0,0}=1\)，ans 就是 \(dp_{n,k,m}\)。

这里需要模，肯定是要使用逆元的。

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 998244353;
int n, m, t, sum;
int w[55], fac[55], dp[55][55][55];

int ksm(int a, int b){//快速幂求逆元
    int res = 1;
    while (b){
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

int C(int a, int b){//组合数
    return fac[a] * ksm(fac[b] * fac[a - b] % mod, mod - 2) % mod;
}

signed main(){
    cin >> n >> m >> t;
    fac[0] = 1;
    for (int i = 1; i <= t; i++) fac[i] = fac[i - 1] * i % mod;
    for (int i = 1; i <= n; i++) cin >> w[i], sum += w[i];
    dp[0][0][0] = 1;//basecase
    for (int i = 1; i <= n; i++){
        dp[i][0][0] = dp[i - 1][0][0];
        for (int j = 1; j <= t; j++){
            for (int k = 1; k <= i; k++){
                dp[i][j][k] = dp[i - 1][j][k];//初始化
                for (int p = 1; p <= j; p++) dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - p][k - 1] * C(j, p) % mod * ksm(w[i], p) % mod * ksm(ksm(sum, p), mod - 2) % mod) % mod;//公式，用逆元
            }
        }
    }
    cout << dp[n][t][m];//ans
    return 0;
}

G

VP 时想到了大部分思路，肯定是 dp。

朴素的想法：\(dp_i\) 表示末尾为 \(i\) 时的答案，转移就是 \(dp_i=\sum_{j=1}^{\sqrt{i}}dp_j\)。

这样子肯定会炸，不难看出只要推到 \(\sqrt{x}\)，就能在一个很小的复杂度内求出 \(x\) 的答案。但是还是有问题。

按照上面的思路，其实可以再分一次，也就是 \(dp_j=\sum_{k=1}^{\sqrt{j}}dp_k\)，现在不会炸了，但是答案的计算就成了问题。

肯定要 \(O(1)\) 计算答案，那就得去找规律。我们发现只有 \(\sqrt{j} \ge k\) 时，才能计算到 \(k\)，所以 \(k\) 的贡献就是 \(k^2\) 到 \(j\) 的最大值 \(\sqrt{i}\)。

最后答案很显然了，就是 \(\sum_{i=1}^{\sqrt{\sqrt{x}}} (\sqrt{x}-i^2+1)\times dp_i\)，需要预处理一下 \(\sqrt{\sqrt{x}}\) 一下的 \(dp\) 值。

这里开根号的时候一定要转 long double，不然精度会爆！！！

AC code:

#include <bits/stdc++.h>
#define int long long
using namespace std;

int t, x;
int dp[100005];

signed main(){
    cin >> t;
    dp[1] = 1;
    for (int i = 2; i <= 1e5; i++){
        for (int j = 1; j <= sqrt((long double)i); j++) dp[i] += dp[j];//预处理一下小的
    }
    for (int _ = 1; _ <= t; _++){
        cin >> x;
        int tmp = sqrt((long double)x), ans = 0;
        for (int i = 1; i <= sqrt((long double)tmp); i++) ans += (tmp - i * i + 1) * dp[i];//根据公式计算答案
        cout << ans << endl;
    }
    return 0;
}