重学线性基

关于我暑假学的，但是完全没学。

我不会线代，所以有关那个的部分直接跳了。

定义

关于这是个啥，我只找到一个还算确切的定义

对于一个序列 $a_{1 \dots n}$，如果一个序列 $d_{1\dots k}$ 满足如下性质，那就称 $d$ 为 $a$ 的一组线性基

1. 能通过 $a$ 异或出的数字也都能通过 $d$ 的一堆子集异或出来。
2. $d$ 的任意一些元素不能异或出 $0$
3. 满足前两条的条件下元素数量最少

这难道不是性质？

反正线性基是一种可爱的解决子集异或的问题的数据结构（？）

构造

上代码

void ins(ll x)
{
	for(int i=59;i>=0;i--)
	{
		if(!(x&(1ll<<i))) continue;
		if(!d[i]) {d[i]=x;break;}
		x^=d[i];
	}
}

我试图解释但是语言笨拙解释不清。

考虑将一个数字插入线性基。从高位向低位枚举，如果当前位是 $0$ 的话直接跳过，如果是 $1$ 的话看当前位有没有插入数字。如果有，直接将数字异或上存储的数字，否则，直接把当前数字留在这里，然后退出。

至于为什么能满足上面的性质：

1. $a\oplus b=c$ 可以得到 $a\oplus c=b$，所以 $x\oplus d_i=d_j$（由构造方式得出），也可以得到 $d_i \oplus d_j=x$，那么原序列中的任意一个数都可以由线性基的一些数异或出来，那么由原序列的一些数异或出的结果也可以由线性基里的一些数得到。
2. 如果 $d_i\oplus d_j\oplus d_k=0$ ，假设 $d_k$ 是最后一个被插入的，那么 $d_k$ 在沿途一定会经过 $d_i,d_j$，这时候 $d_k$ 会被削成 $0$。
3. 明天证wwww

这玩意咋用

其实能干的事情还是挺多的。

序列中子集能异或的最大值

从高位向低位枚举，假如异或上当前的数字会让答案变大，就异或就可以了

理由是这是一种贪心。

从高位开始，到这一位，这里会确定当前位的二进制数字，而之后的数都不会影响这一位了，所以如果改变当前位会让结果变大，那一定要选上。

序列中子集能异或出的最小值

如果插入的过程出现了某个元素插不进去，就直接是 $0$。

因为这样一定是出现了能异或出 $0$ 的情况，就是某些数异或完了是另外一个元素。

否则直接取出线性基里的最小值就行了，因为别的数都有比最小值的最高位还要高的 $1$。选那些就一定不优。

一个数跟子集中的某些数能异或出的最大/最小值

和取最大值的思路一样，就从高位向低位枚举，答案变优了就直接选就行了。理由和上面一样。

例题

板子之类的跳了。

圣剑护符

线性基中有 $30$ 个空位，那么最坏情况就是每位都依次插入了数，那第 $31$ 个数无论如何都插不进去，我们刚才给的结论是如果有数字插不进去就说明这个数能被表示出来。 所以如果距离大于 $30$ 直接算出来就行，否则一个一个插入就行。 整个树剖套线段树就行。

[WC2011]最大XOR和路径

感觉是个结论的应用。

就是 $1$ 到 $n$ 的路径是直接走到再套上一堆环。

有一张简明的图：

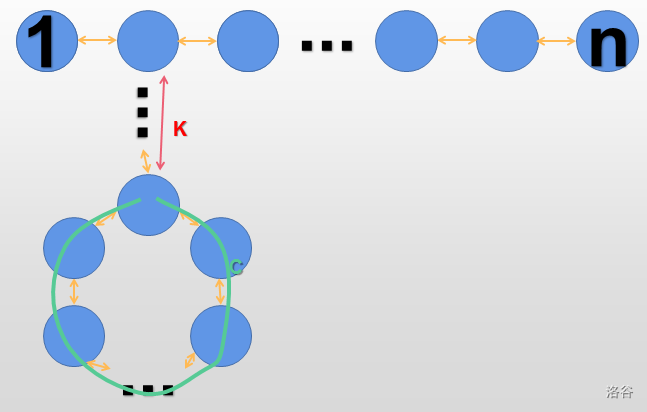
你会发现 $1$ 到 $n$ 经过环的异或和就是链上异或和直接异或环上所有边的异或和。

那么只需要把简单环都扔进线性基，然后找到那条链就行。

但是如果有多条链呢？

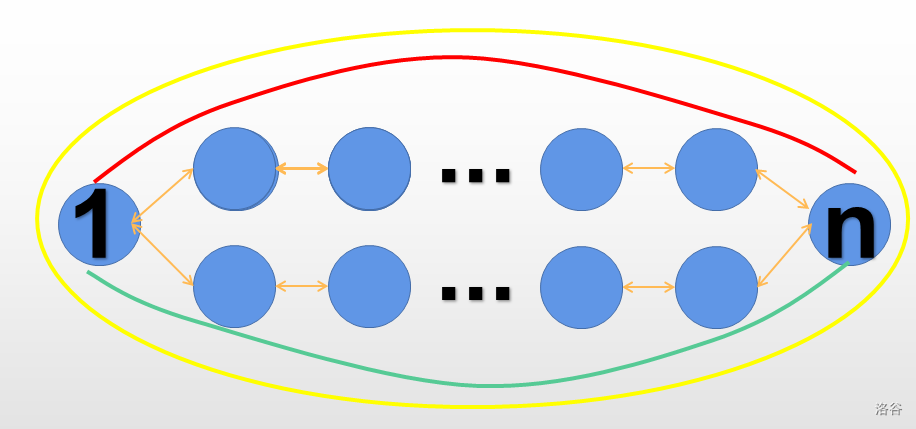
红色的链异或上黄色的环等于绿色的链，所以对答案没有影响。

如果有环套环也没关系，即使没有办法把所有的环找到，两个环异或一下会得到相互套着的另一个环

ABC249G

起因。

把 $a$ 和 $b$ 放在一起高斯消元是神奇的。

这样也相当于放在线性基里。

然后只剩下 $60$ 个本质不同的卡片。

然后从高到低先尽可能选卡片让 $a$ 的部分接近 $K$。

选完之后对 $a$ 不产生影响的卡片随便选，使得跟之前的答案最大。

然后从低位到高位依次放弃卡片，如果这张卡片之前选了，就直接看这张卡片之后能产生的最大答案，否则如果 $K$ 这一位是 $1$ ，那后面也可以随便选。

link

---

我不写了！

撸猫是快乐的！！！！

ABC是好的！！！！！