9.20 小记
[COCI2020] Semafor
tag :矩阵乘法
做完这道题,我发现我对矩乘的理解还是太浅薄了
首先,每次操作都是可以转化成一次异或卷积。因为每种状态都可以看作是一个二进制数,两个二进制数异或后就是另外一种状态。而这两个状态合起来的贡献就是相乘的数值
这样 \(K\) 次操作可以进行矩阵快速幂来优化。那么现在的问题是每 \(K\) 次都要保证所有的状态是合法的。如果做 \(\frac n K\) 次,每次清空不合法的状态的话复杂度还是炸裂。所以我们需要考虑优化一下。
我们考虑把 \(K\) 次转移后的结果都压成一个矩阵,这个矩阵的含义就是从 \(i\) 转移到到 \(j\) 的合法方案数,其中 \(i\) 和 \(j\) 都是数字,而不是刚才的二进制状态。这样进行 \(\lfloor \frac n K \rfloor\times K\) 次转移就可以用这个矩阵来进行快速幂,而剩下 \(n\% K\) 的部分就可以转化回二进制状态来进行快速幂。
我们来捋一下维护的东西和过程:
- 先预处理 \(K\) 次异或卷积,运用快速幂,得到 \(f_{i}\) 为在进行 \(K\) 次操作后从 \(0\) 到另一个二进制状态为 \(i\) 的的方案数
- 再把结果压成矩阵,设 \(g_{i,j}\) 表示 \(K\) 次操作后从数字 \(i\) 转移到数字 \(j\) 的方案数,\(g_{i,j}=f_{mp_i\oplus mp_j}\),\(mp_i\) 表示数字 \(i\) 的二进制状态表示。然后和一个只有 \(g_{x,x}=1\) 其余为 \(0\) 的矩阵乘 \(\frac n K\) 次,同样用快速幂
- 把得到的矩阵转回二进制状态表示,再进行 \(n\%K\) 次异或卷积
这样,这道题就做完了,答案就是输出每个数字的二进制表示下的异或卷积之后的结果。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,K;int m,X;int sz,num,mx;
int mp[]={3,1,6,21,9,28,18,5,30,29};//每个数的二进制状态表示
ll b[102][102],g[102][102],tt[102][102];
struct martix
{
ll p[1025];int siz;
martix (int xx){siz=xx;for(int i=0;i<xx;i++) p[i]=0;}
};
const int mod=1e9+7;
void mul(martix &a,martix &f,martix &t)
{
for(int i=0;i<mx;i++)
{
if(!a.p[i]) continue;
for(int j=0;j<mx;j++)
{
if(!f.p[j]) continue;
t.p[i^j]=(t.p[i^j]+a.p[i]*f.p[j]%mod)%mod;
}
}
for(int i=0;i<mx;i++)
a.p[i]=t.p[i],t.p[i]=0;
}
void ksm1(martix &a,martix &f,ll K)//异或卷积的快速幂
{
martix t(a.siz);memset(t.p,0,sizeof(t.p));
while(K)
{
if(K&1) mul(f,a,t);
mul(a,a,t);K>>=1;
}
}
void ksm2(ll K)//矩阵乘法的快速幂
{
while(K)
{
if(K&1)
{
for(int k=0;k<num;k++)
{
for(int i=0;i<num;i++)
{
if(!g[i][k]) continue;
for(int j=0;j<num;j++)
{
if(!b[k][j]) continue;
tt[i][j]=(tt[i][j]+g[i][k]*b[k][j]%mod)%mod;
}
}
}
for(int i=0;i<num;i++) for(int j=0;j<num;j++) g[i][j]=tt[i][j],tt[i][j]=0;
}
for(int k=0;k<num;k++)
{
for(int i=0;i<num;i++)
{
if(!b[i][k]) continue;
for(int j=0;j<num;j++)
{
if(!b[k][j]) continue;
tt[i][j]=(tt[i][j]+b[i][k]*b[k][j]%mod)%mod;
}
}
}
for(int i=0;i<num;i++) for(int j=0;j<num;j++) b[i][j]=tt[i][j],tt[i][j]=0;
K>>=1;
}
}
int find(int x){return (m==1)?mp[x]:((mp[x/10]<<5)|mp[x%10]);}
int main()
{
// freopen("p.in","r",stdin);
scanf("%d%lld%lld%d",&m,&n,&K,&X);
if(m==1) sz=5,num=10,mx=32;else sz=10,num=100,mx=1024;
martix a(mx),t(mx);
memset(a.p,0,sizeof(a.p));memset(t.p,0,sizeof(t.p));
for(int i=0;i<sz;i++) a.p[1<<i]=1;
martix f(mx);memset(f.p,0,sizeof(f.p));f.p[0]=1;ksm1(a,f,K);
for(int i=0;i<num;i++)
{
for(int j=0;j<num;j++)
b[i][j]=f.p[find(i)^find(j)];//把结果压成矩阵
}
g[X][X]=1; ksm2(n/K);
martix ans(mx);memset(ans.p,0,sizeof(ans.p));
for(int i=0;i<num;i++) ans.p[find(i)]=g[X][i];//把矩阵的结果转化回二进制状态
memset(a.p,0,sizeof(a.p));memset(f.p,0,sizeof(f.p));
for(int i=0;i<sz;i++) a.p[1<<i]=1;
f.p[0]=1;ksm1(a,f,n%K);
mul(ans,f,t);
for(int i=0;i<num;i++)
{
printf("%lld\n",ans.p[find(i)]);
}
return (0-0);
}
[COCI2020] Zagrade
tag :构造,栈
首先可以知道的是如果 \(l\) 到 \(r\) 是合法的括号序列且 \(l+1\) 到 \(r-1\) 为合法的括号序列,那么 \(l\) 一定是左括号,\(r\) 一定是右括号。
那么我们考虑使用栈,栈里存放尚未匹配的括号。对于当前的 \(i\), 看它到栈顶是否为合法序列,如果是,因为从 \(st[top+1]\) 到 \(i-1\) 的都已经出栈,意味着他们一定都是合法的,所以栈顶一定是左括号,\(i\) 一定是右括号
整个序列都做完后,如果有尚未出栈的元素,就说明他们一定互相匹配不到,就让前一半元素是右括号,后一半是左括号就行了
#include <bits/stdc++.h>
using namespace std;
int n,Q;
int st[200004],ans[200003],top;
bool ask(int x,int y)
{
printf("? %d %d\n",x,y);
fflush(stdout);
int a;scanf("%d",&a);
return a;
}
int main()
{
scanf("%d%d",&n,&Q);
for(int i=1;i<=n;i++)
{
if(!top) {st[++top]=i;continue;}
if(ask(st[top],i))
{
ans[st[top]]=0;ans[i]=1;
top--;
}
else
st[++top]=i;
}
if(top%2!=0) return 0;
for(int i=1;i<=top/2;i++) ans[st[i]]=1;
for(int i=top/2+1;i<=top;i++) ans[st[i]]=0;
printf("! ");
for(int i=1;i<=n;i++)
printf("%c",ans[i]?')':'(');
printf("\n");
fflush(stdout);
return 0;
}
[COCI2019-2020#6] Konstrukcija
鸣谢
感谢 @sssmzy 大佬,没有他我可能这辈子都做不出来
思路
感觉是一道很人类智慧的构造题
如果是一条长度为 \(n+2\) 的链的话,答案就是 \(\displaystyle \sum_{i=1}^n C_{n}^i(-1)^i=(1-1)^n=0\) ,如果只有两个点就是 \(-1\)
所以如果我们构造出这样的图形
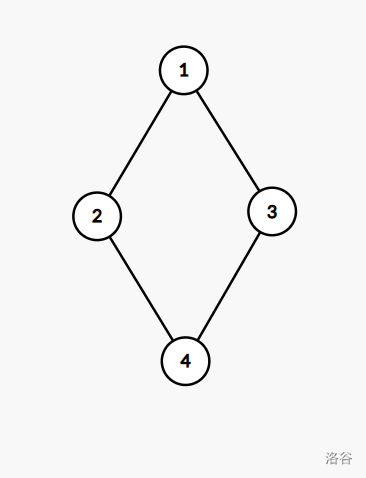
那么从 2 走的和会贡献两次变成 0,从 3 走的和会贡献变成 0 ,但是两次都重复计算了只有 1 和 n 的路径要减回去,所以答案是 1
那么第一个 subtask 就出现了
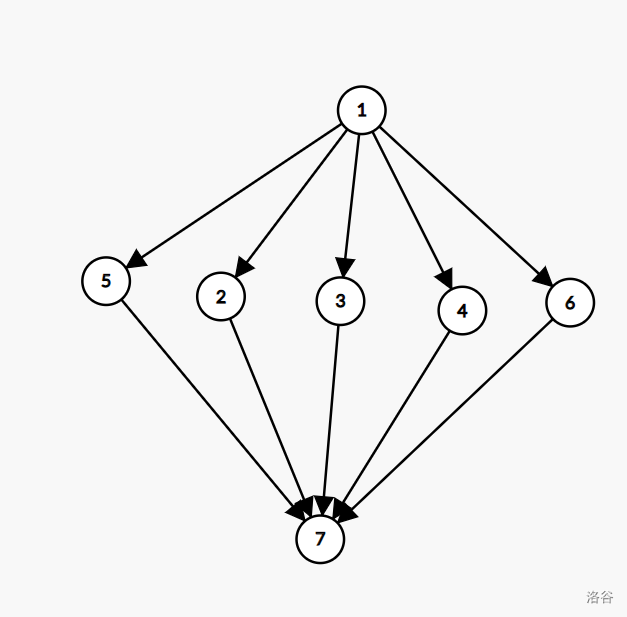
这样如果要求的答案是 \(x\),那么只需要在中间构造 \(x+1\) 个新节点就可以了。
那么现在我们考虑如何构造负数。
我们考虑第一层是相当于乘上了个整数,那么第二层因为奇偶性的变化,他会变成与原来正负性相反的东西
这样说有点抽象,我们挂一张图
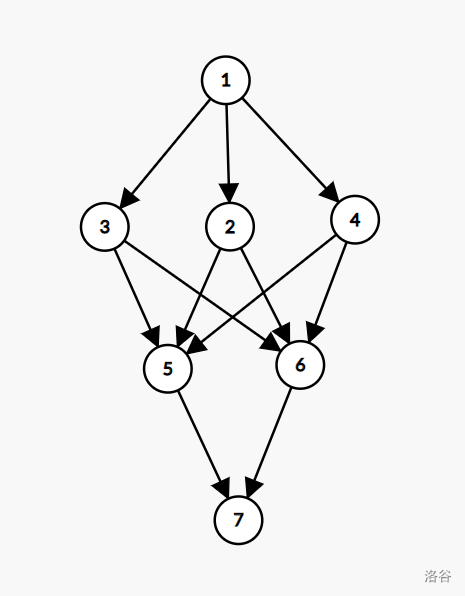
其中 5,6 作为第二层插入到图中,他们的加入使得原来的路径都增加了一种可以让原来的值变成负数的方案,如果只增加一个点,那么原来的值会加上他们的相反数变成 0 ,而增加两个点会让原来的值增加两个相反数使得正负性相反。
所以构造负数就是在第一层构造原数,第二层加上两个点变成相反数
这样第二个 subtask 就做完了。
但再往后会点数和边数都会炸裂。我们考虑继续优化
其实你观察上面这张图,就相当于在第一层乘了 2 ,第二层乘了 -1。所以以此类推,假设我们在第 \(i\) 层加入了 \(j\) 个点,就相当于在原答案上乘了 \((j-i)\times (-1)^i\)
但是你不能像分解质因子那样分解,因为如果是一个很大的质数照样把你卡炸 =_=
我们考虑把一个数相乘二进制,把每一层看成 2 的整数次幂,这样只有 \(\log\) 层,每层只有 3 个数,每个数会连出去 3 条边
如果到最后正负性错了你就需要在最后一层加上两个节点,相当于乘 -1
然后难点就是怎样把二进制中为 0 的部分去掉
然后你可以这样
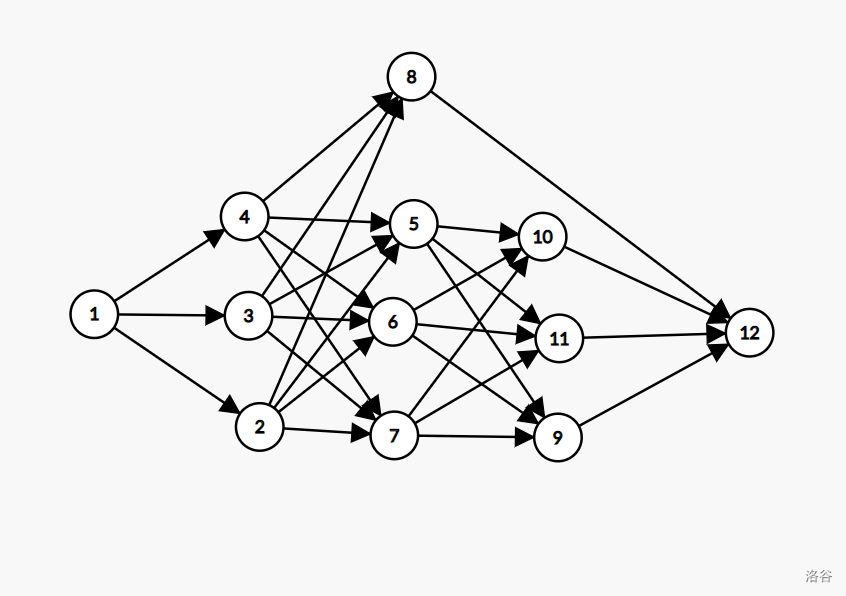
在某一层连出去了一个 8 号节点。这样就会多出一些序列包含 8,这样其实相当于把整个第一层的贡献乘 -1 再加回去。
就拿这张图来说,第一层的贡献是 \(2^0=1\) ,然后如果加上 8 这个节点,第一层就会减去 \(2^0\) ,而且这样不影响后面的权值的计算。
但是这样会出问题
就是当出现这样的情况:
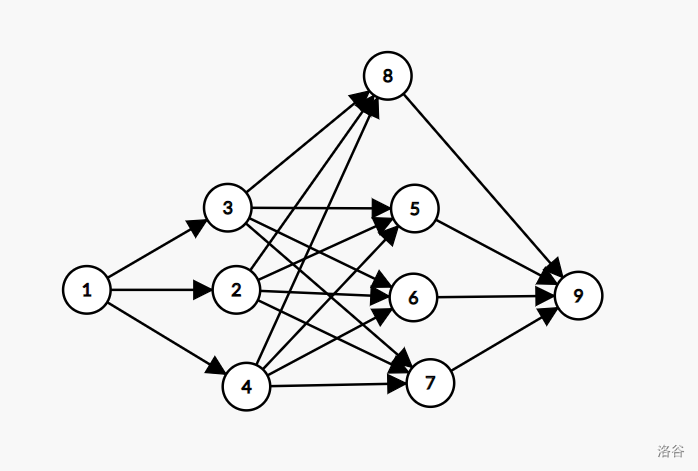
在这张图中,第一层的贡献还是 \(2^0=1\) ,然后需要加上 8 节点之后第一层的贡献被消除掉了。但是在后面的计算中,第二层是乘 -2,所以对于第二层来说,需要再加上第一层的值才能消除掉第一层的贡献,而不是减去第一层的值。所以这样是有问题的。
在什么时候会出现这样的情况?
其实就是在 \(K\) 为负数时,并且当前层乘上去后是整数,或者原数是正数,并且当前层乘完了是负数。因为在最后把那一层的贡献消除的过程中,如果正负性不同,就说明不能通过乘 -1 消除贡献。
然后我们考虑怎样解决这种情况。
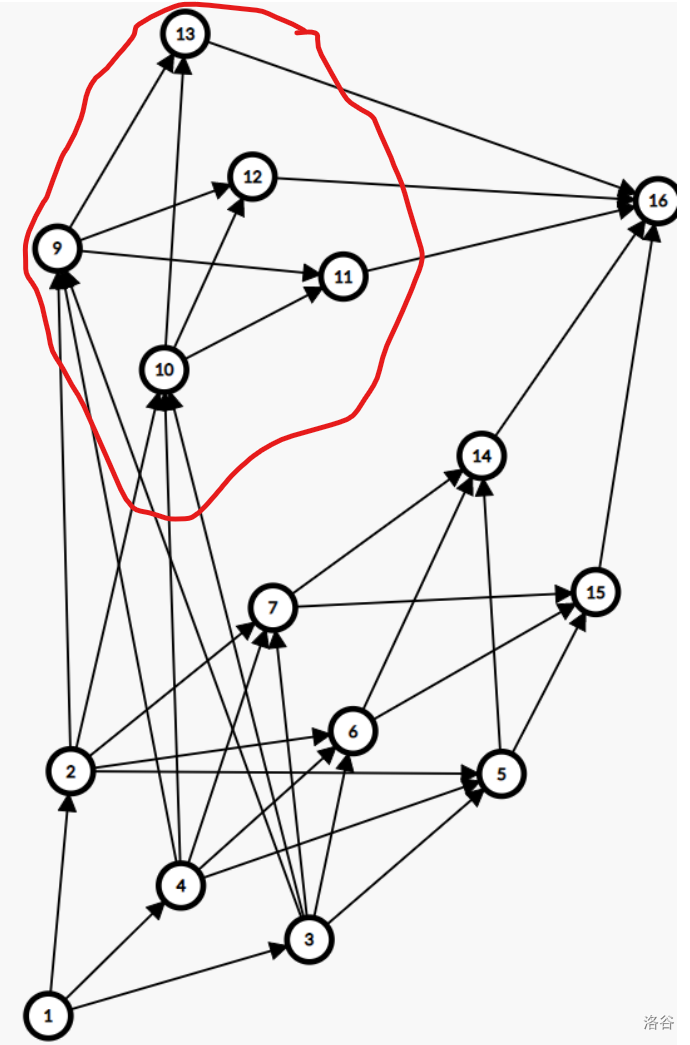
这是一种想法。因为加上红色圈里的五个点后,-1 的贡献多了 5 个,1 的贡献多了 6 个,这样就是对的了。
但是这只能过 subtask 3,它会被卡个几十条边
那么换一种方法!
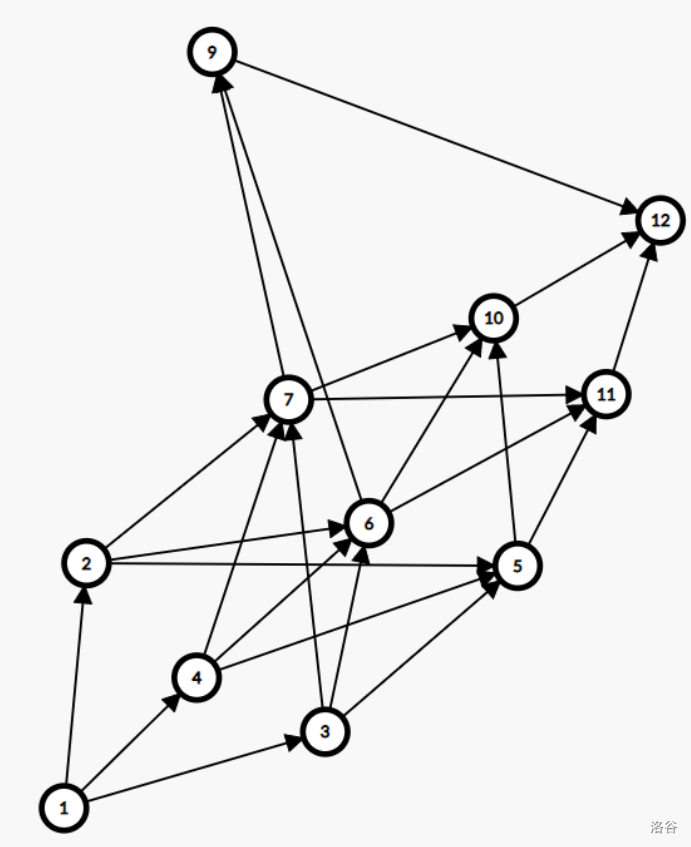
这样的话,对于第一层的贡献 9 节点会让它乘一次 -1 ,6,7 节点会让它贡献两次乘 1 的情况,所以这样也是加上了第一层的贡献。
所以到这里,这道题的构造方法就讲完啦。
需要注意的细节主要还是在第一层和最后一层的特判什么的。
code
if(K<0) K=-K,typ=1; int dep=0;ls=1;
while(K)
{
dep++;
bool flag=0;
if(K&1)
{
if(K!=1)
{
if(!((dep&1)^typ)) flag=1;
else
{
if(ls==1) add(1,++cnt);
else add(ls,++cnt),add(ls+1,cnt),add(ls+2,cnt);
add(cnt,1001);
}
}
else
{
if(((dep&1)^typ))
{
if(ls==1) add(1,++cnt),add(1,++cnt);
else add(ls,++cnt),add(ls+1,cnt),add(ls+2,cnt),add(ls,++cnt),add(ls+1,cnt),add(ls+2,cnt);
add(cnt-1,1001);add(cnt,1001);
}
else add(ls,1001),add(ls+1,1001),add(ls+2,1001);
}
}
K>>=1;
if(K)
{
if(dep==1) cnt++,add(1,cnt),cnt++,add(1,cnt),cnt++,add(1,cnt);
else cnt++,add(ls,cnt),add(ls+1,cnt),add(ls+2,cnt),cnt++,add(ls,cnt),add(ls+1,cnt),add(ls+2,cnt),cnt++,add(ls,cnt),add(ls+1,cnt),add(ls+2,cnt);
ls=cnt-2;
if(flag) add(ls,++cnt),add(ls+1,cnt),add(cnt,1001);
}
}
废话
不要阴间构造不要阴间构造
自由的夏虫编织着美梦解渴
单薄的外壳 展开花纹 尽将内心诉说
鞘翅振涌 卷起击碎定论的漩涡
等待 数百天伏蛰 这一瞬冲破
最高亢的歌 予我
肆意鸣唱 直到 嘶哑那刻



 浙公网安备 33010602011771号
浙公网安备 33010602011771号