数论模板复习

基本结论：

费马小定理：若p为质数，则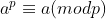

 欧拉定理：若a,n互质，则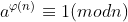

 欧拉函数计算公式：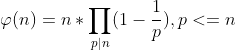

 

扩展欧几里得算法（Exgcd）

计算不定方程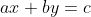的一组特解。

由贝祖定理，上方程有解当且仅当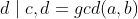时有解。代码中exgcd函数求出的是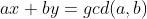的解。将其乘上c/d即可得到原方程的解。

设x'_,y'为方程的一组特解，则方程通解可表示为：

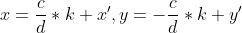
代码：

int a,b,c,d,t,x,y;
int exgcd(int a,int b,int &x,int &y) {
    if(b == 0) {
        x=1; y=0; return a;
    }
    int dd=exgcd(b,a%b,x,y),xx=x;
    x=y; y=xx-(a/b)*y;
    return dd;
}
int main() {
    a=read(); b=read(); c=read();
    x=0; y=0;
    d=exgcd(a,b,x,y);
    if(c % d) {
        printf("-1\n");
    }
    x=x*b/d; y=y*a/d;
    printf("%d %d ",x,y);
}

上文代码不能保证x非负。若要得到x的最小正整数解，还要加入下面这句话：

x=(x % b +b)%b;

对于线性同余方程 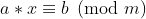,我们可以将其转化成不定方程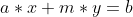来求解

 

乘法逆元

用于将取模时的除法运算转换成乘法运算。即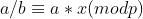中的x.

求法：

1.费马小定理+快速幂

a,p互质时，逆元即为a^p-2(mod p)

2.exgcd

即求解同余方程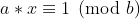  

3.线性递推求1~n中每个数的逆元

    inv[1]=1;
    for(int i=2;i<=n;i++) {
        inv[i]=(p-p/i)%p*inv[p%i];
        printf("%d\n",inv[i]);
    }

 

中国剩余定理

 用于求解如下同余方程组：

解法：

当m_i两两互质时，有：

 

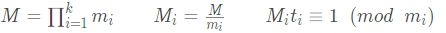
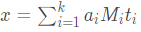
任意解即为 x+k*M.

代码：

ll M[N],a[N],m[N],mm;
ll x,y,d,ans;
ll exgcd(ll a,ll b,ll &x,ll &y) {
    if(b == 0) {
        x=1; y=0; return a;
    }
    ll dd=exgcd(b,a%b,x,y),xx=x;
    x=y; y=xx-(a/b)*y;
    return dd;
}
int main() {
    for(int i=1;i<=n;i++) {
        m[i]=read(); mm*=m[i]; a[i]=read();
    }
    for(int i=1;i<=n;i++) {
        M[i]=mm/m[i];
        x=0; y=0;
        d=exgcd(M[i],m[i],x,y);
        x=(x%m[i]+m[i])%m[i];
        ans+=x*M[i]*a[i];
    }
}

当m_i不互质时，我们仍可以通过使用k次exgcd来求出这个解。

代码：

 

 

杂项

快速幂：

long long qpow(int a,int b,int p) {
    ll x=a,ans=1;
    while(b) {
        if(b & 1) ans=ans*x%p;
        x=x*x%p;
        k>>=1;
    }
    return ans;
}

等比数列求和：

1.分治

2.公式+逆元