2021 HZ国庆集训DAY1笔记——杂题选讲1

话说这好像还是我第一次听hkk神仙讲课呢......

结果hkk把ppt标题打错了，害的一群人早上半天全在想DP......

热身题

T1：CCPC2021 网络赛 F

难度：D1T1

签到题，注意到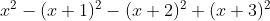的值为4，所以我们对n%4进行分类。代码如下：

 

#include<iostream>
using namespace std;
#define il inline
int read() {
    int s=0,w=1; char ch=getchar();
    while(ch<'0' || ch>'9') { if(ch=='-') w=-1; ch=getchar();}
    while(ch>='0' && ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
} 
int t,n;
void solve(int n) {
    int k=n%4;
    if(k==0) printf("%d\n",n);
    if(k==1) printf("%d\n1",n);
    if(k==2) printf("%d\n0001",n+2);
    if(k==3) printf("%d\n01",n-1);
    for(int i=1;i*4<=n;i++) printf("1001");
    printf("\n");
    return;
}
int main() {
//    freopen()
    t=read();
    while(t) {
        t--;
        n=read();
        solve(n);
    }
    return 0;
}

 

T2：CCPC2021 网络赛 G

难度：D1T2

因为g(999999)=54，所以对于任意n<=1e6，都有g(n)<=54。所以对于每一组(A,B,C,D)，我们可以穷举g(x)的取值，这样我们就可以得到一个关于x的二次函数。提前预处理出g(x)的每个值对应的x的取值，根据二次项前的系数求出距对称轴最远/近的点，即为答案。

代码：待补（×）

 

T3：原题： CCPC2021 网络赛 K

难度：D1T2

不算很难想的DP，但细节真的很多。以列数作为阶段，用f(i,j)表示打到第i列，用掉j发子弹的最优值。提前预处理出每一列用掉j发子弹时的最优值。此时注意，因为可能打完最后一枪后又奖励了一发子弹，这两种情况对后续状态的贡献是不一样的。所以我们需要预处理两个东西，一是最后一发子弹打在当列时的最优值，二是最后一发子弹被奖励回来时的最优值。同理，dp数组也应该开两个。

代码（有点小问题等我有空再改）：

#include<bits/stdc++.h>
using namespace std;
#define il inline
int read() {
    int s=0,w=1; char ch=getchar();
    while(ch<'0' || ch>'9') { if(ch=='-') w=-1; ch=getchar();}
    while(ch>='0' && ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
} 
int n,m,k,t;
int a[202][202],is[202][202],fn[202][202],fy[202][202],dpn[202][202],dpy[202][202],ans;
void init() {
    memset(fn,0,sizeof(fn));
    memset(dpn,0,sizeof(dpn));
    memset(fy,0,sizeof(fy));
    memset(dpy,0,sizeof(dpy));
    ans=0;
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++) {
            char ch;
            scanf("%d %c",&a[i][j],&ch);         
            if(ch=='Y') is[i][j]=1;            
        }
    }
}
void work() {
    for(int i=1;i<=m;i++) {
        int cnt=0;
        for(int j=n;j>=1;j--) {
            if(is[i][j]) fy[i][cnt]+=a[j][i];        
            else {
                cnt++;
                fy[i][cnt]=fy[i][cnt-1]+a[j][i];      
                fn[i][cnt]=fy[i][cnt-1]+a[j][i];         
            }              
        }
    }
    
    for(int i=1;i<=m;i++) { 
        for(int j=0;j<=k;j++) { 
            for(int r=0;r<=j && r<=n;r++) { 
                dpy[i][j]=max(dpy[i][j],dpy[i-1][j-r]+fy[i][r]);       
                if(r) dpn[i][j]=max(dpn[i][j],dpn[i-1][j-r]+fn[i][r]);  
                if(j-r) dpn[i][j]=max(dpn[i][j],dpn[i-1][j-r]+fy[i][r]); 
            } 
        } 
    } 
    
} 
int main() {
//    t=read();
//    while(t--) {
        n=read(); m=read(); k=read();  
        init();              
        work();         
        printf("%d\n",max(dpy[m][k],dpn[m][k]));  
//    }
    return 0;
}

 

T4： ICPC2021 网络赛Ⅱ K

难度：D2T2

（你管这叫热身？）这个n的规模一眼状压。设s为已经取走的菜的集合，f(i,s,j)表示第i个人在已选菜集合为s时选择j菜的概率，对于每个状态，我们直接枚举当前能选择的菜，用刷表法更新（有点像前两天写的宝藏）

代码：待补 

 

正式题

（渐渐开始毒瘤）

T1： CCPC2021 网络赛 L

难度：D2T1

设f(n)删掉n个石子时的最小步数。我们通过打（cai）表（ce）可知，f(n)非严格单调递增。（具体证明可参考 这篇博客）这样我们就有了一个显然的贪心思想，每次优先选择选择n mod p 最大的方案，则有f(n)=f(n-(n mod p))+1。现在的问题在于，如何找到这样的p。在n+1不是p的倍数的情况下，n+1 mod p的值即为(n mod p)+1。所以我们使用链表来存储这些质数。当n++时，我们对n的质因子采取暴力修改接到链表尾部，这样每次直接取出链表头部求出f(n)即可。

代码：

#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ll long long
//debug
void dg() { printf("114514 ");}
void print(int x) { printf("%d ",x);}
//
il int read() {
    int s=0,w=1; char ch=getchar();
    while(ch<'0' || ch>'9') { if(ch=='-') w=-1; ch=getchar();}
    while(ch<='9' &&  ch>='0') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
const int N=2e6+5;
const int M=1e5+5;
int t,n,m,vis[N],f[N];
vector<int> num[N];
void prework() {
    for(int i=2;i<=2e6;i++) {
        if(vis[i]) continue;
        num[i].push_back(i);
        for(int j=i;j<=2e6/i;j++) {
            vis[i*j]=1;  
            num[i*j].push_back(i);
            if(i*j>N) dg();
        }
    }
    f[1]=1;
    return;
}
struct node{
    int prev,nex,val;
} p[M]; int head,tail;
bool cmp(node a,node b) {
    return a.val<b.val;
}
void change(int k) {
    p[p[k].prev].nex=p[k].nex;
    p[p[k].nex].prev=p[k].prev;//删掉 
    
    p[k].prev=p[tail].prev;
    p[k].nex=tail; //更改k位置指针 
    
    p[p[tail].prev].nex=k;
    p[tail].prev=k; //将k插入末尾 
}
void deal() {
    memset(vis,0,sizeof(vis));
    sort(p+1,p+m+1,cmp);
    for(int i=1;i<=m;i++) {
        p[i].prev=i-1; p[i].nex=i+1; vis[p[i].val]=i;
    }
    head=0; tail=m+1;
    p[head].nex=1; p[tail].prev=m;
    for(int i=2;i<=n;i++) {
        for(int j=0;j<num[i].size();j++) if(vis[num[i][j]]) change(vis[num[i][j]]);          
        f[i]=f[i-(i%p[p[head].nex].val)]+1;                             
    }
    return;
}
int main() {
    t=read();
    prework();
    while(t) {
        t--;
        n=read(); m=read();
        for(int i=1;i<=m;i++) p[i].val=read();
        deal(); 
        for(int i=1;i<=n;i++) printf("%d ",f[i]);  
        printf("\n"); 
    }
    return 0;
}

 

 

 

 

T2：CCPC2021 网络赛 H

难度：D1T3

不考虑存在更大的公因数的情况下，若v(l,r)=x，则区间(l,r)中至少含有两个x的倍数。“至少”这种东西数据结构很难维护，我们考虑它的互补问题，求只含有1个或不含有x的倍数的区间数。

我们从大到小枚举x的值，维护对于每一个r，我们用线段树维护使v(l,r)<x的最小l。具体实现......貌似要用到Segmenttreebeats。暂时不会，先空着。

代码：待补

 

T3：ICPC2021 网络赛 J

 没听懂，先空着

 

T4：ICPC2021 网络赛 E

难度：D2T1

线段树维护dfs序的板子，没啥好说的

代码：略

 

T5：ICPC2021 网络赛 II H

难度：D1T2

愚人节题？构造方法：每个集合随机塞 512/r个数，可以证明不满足题意的可能性小到可以忽略不计。

代码：略

 

T6：ICPC2021 网络赛 II L

毒瘤数据结构，不会，跳过

 

T6：CF1580C

不会根号分治，跳过

 

T7：CF1580D

神仙DP，不会，跳过

 

附加题：CF1580E

推式子，最后的结果是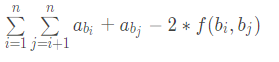，会发现这其实是树上两点的距离公式，所以只需要构造出一棵任意两节点的lca是两点路径上的最小值的树就行了。这是啥？笛卡尔树。

代码：待补