【SCOI2010】股票交易 题解 (洛谷P2569)

一道很好的DP题。

原题：https://www.luogu.com.cn/problem/P2569

题意：太长就不概括了，自己把题目好好读几遍，我一开始做的时候就把题意读错了...

解析：

看样子就知道是个DP（笑）。显然以天数为阶段，再看看范围，2000*2000完全可以跑，状态的第二个维度很容易想到用手上的股票数来表示。设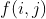表示到第i天为止，手上有j张股票时获得的最大利润。下面我们来考虑

这个状态该如何转移。

我们对第i天可以进行的操作进行分类讨论。

1.手上本来没有股票，直接买j张，则有转移方程：

 

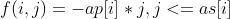
 2. 不进行操作，所以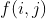的值直接从上一天转移即可，方程如下：

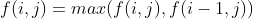
3.买入股票。此时的情况较为复杂。因为两次操作最小时间间隔为w天，所以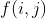的值应该由第i-w-1 天转移得到。我们可以枚举那天时手上的的股票数k（此处只能枚举那天拥有的股票数，而不是第i天买入的股票数，否则得到的方程无法优化），则不难写出如下方程：

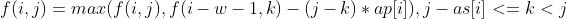
 4.卖出股票，则与上种情况类似：

  

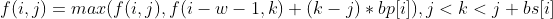
  这样，我们就得到了该题的全部方程。不过，再一看，这个方程的复杂度是O(n³)，显然不能通过2000的数据。我们需要对其进行优化。对3中的式子变形可得到：

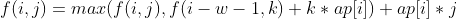
对于一个阶段i，f(i,j)与ap[i]均可以看做常数项，max函数中的项只与k有关。而随着j的变大，k的取值范围也随之变大而不缩小。对于这样的问题我们显然可以使用单调队列来优化（不会单调队列的亲请百度哦）

4中的式子变形后的结果和3差不多，请读者自行推导，不过要注意范围哦（）

DP部分核心代码：

for(int i=0;i<=t;i++)
    for(int j=0;j<=maxp;j++) f[i][j]=-Inf;
    for(int i=1;i<=t;i++) {
        for(int j=0;j<=maxp && j<=as[i];j++) f[i][j]=-ap[i]*j;
        for(int j=0;j<=maxp;j++) f[i][j]=max(f[i][j],f[i-1][j]);
        if(i>w) {
            l=1; r=0; 
            for(int j=0;j<=maxp;j++) {
                while(l<=r && q[l]<j-as[i]) l++;
                while(l<=r && f[i-w-1][j]+j*ap[i]>=f[i-w-1][q[r]]+q[r]*ap[i]) r--;
                q[++r]=j;
                if(l<=r)
                    f[i][j]=max(f[i][j],f[i-w-1][q[l]]+q[l]*ap[i]-ap[i]*j);
            }
            
            l=1; r=0;
            for(int j=maxp;j>=0;j--) {
                while(l<=r && q[l]>j+bs[i]) l++;
                while(l<=r && f[i-w-1][j]+j*bp[i]>=f[i-w-1][q[r]]+q[r]*bp[i]) r--;
                q[++r]=j;
                if(l<=r)
                    f[i][j]=max(f[i][j],f[i-w-1][q[l]]+q[l]*bp[i]-bp[i]*j);
            }
        }
    }

 

 答案的话，最后一天手上可以留任意张股票，所以有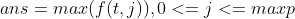（事实上，f(t,0)就是答案，读者可以自行思考证明）

完结撒花。