数据库设计范式

数据库设计范式也就是数据库设计的规范化形式。

 

关系的第一范式（1NF）：若关系模式R(U)中关系的每个分量都是不可分的数据项（值，原子），则称R(U)属于第一范式，记为：R(U) € 1NF。

例如：Star(name, address(street, city))，Star不属于1NF，因为属性address仍包含了street和city两个属性，其分量不是原子。

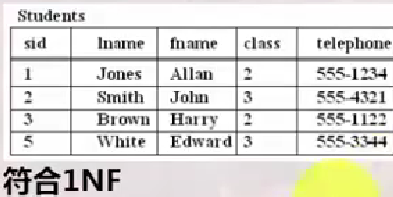
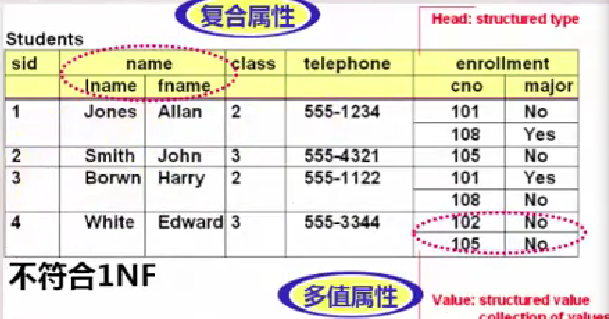
如图：左图严格按照行和列进行管理，满足第一范式；右图存在可再分属性，不满足第一范式。

INF要求关系中不能有复合属性、多值属性及其组合。

 

关系的第二范式（2NF）：若R(U) € 1NF且U中的每一非主属性完全函数依赖于候选键，则称R(U)属于第二范式，记为R(U) € 2NF。

候选键：能够完全决定所有属性的一个属性或属性组，候选键本质上是一个属性或者属性组。

非主属性：都包含在任何候选键中的属性。

完全函数依赖：若x决定y，则x的任何一个真子集x^'都不能决定y，则x为y的完全函数依赖。

例如：R(S#,SN,SD,CN,G)，其中，S#是学号,SN:姓名,SD:班级,CN:课程,G:成绩。函数依赖:S#→SN,S#→SD,{S#,CN}→G; 候选键:{S#,CN}; 非主属性:SN、SD和G。因为:存在部分依赖，{S#,CN}部分决定{SN,SD}，也就是S#就可以决定{SN,SD}，不满足完全决定，所以R不属于2NF。将其分解为R₁(S#,SN,SD),R₂(S#,CN,G)，则R₁和R₂都属于第二范式。

第二范式消除了非主属性对候选键的部分依赖。

 

关系的第三范式（3NF）：若R(U,F)∈2NF且R中不存在这样的情况：候选键X，属性组Y⊆U和非属性组A，且A∉X,A∉Y,Y⊄X,Y不决定X，使得X→Y,Y→A成立。满足以上条件则称R(U)属于第三范式，记为：R(U)∈3NF。

简单来说，第三范式就是在满足第二范式基础上没有传递函数依赖的范式。

例如：Store(Sid,Pid,Did,Mgr),其中，Sid:商店, Pid:商品, Did:经营部， Mgr:经理。函数依赖：{Sid,Pid}→Did, {Sid,Did}→Mgr；候选键{Sid,Pid}，非主属性:Mgr。因为{Sid,Pid}→Did, {Sid,Did}→Mgr，Mgr传递依赖于Sid,Pid，所以R不属于3NF。将其分解为R₁(Sid,Pid,Did)，R₂(Sid,Did,Mgr)，则R1和R2都属于3NF。

第三范式消除了非主属性对候选键的传递依赖。

 

关系的BC范式（BCNF）：若R(U,F)∈1NF，若对于任何X→Y∈F(或X→A∈F)，当Y⊄X(或A∉X)时，X必含有候选键，则称R(U)属于Boyce-Codd范式，记为：R(U)∈BCNF。

若R(U,F)∈BCNF，则R(U,F)∈3NF。

满足BC范式，则一定满足第三范式；满足第三范式不一定满足BC范式。

 

关系的第四范式（4NF）：设R(U,F)∈1NF，D是其上的一组依赖（函数依赖，多值依赖），对任意X→→Y∈D，若Y≠ø，Y⊄X，XY≠U，必有X为超键，则称R(U)满足第四范式，记为：R(U)∈4NF。

多值依赖：

第四范式消除了非主键属性对候选键以外属性的多值依赖；如果有多值依赖，则一定依赖于候选键。

若R(U,F)∈4NF，则R(U,F)∈BCNF。

满足第四范式，则一定满足BC范式；满足BC范式不一定满足第四范式。

若R上仅存在函数依赖，则若R(U,F)∈4NF，则R(U,F)∈BCNF；反之，若R(U,F)∈BCNF，则R(U,F)∈4NF。

 

关系的弱第四范式（W4NF）：设R(U,F)∈3NF，若R上的任何互补多值依赖X→→Y(XY≠U,Y-X≠ø)和X→→(U-X-Y)中必有一个是函数依赖，则称R是弱第四范式，记为：R(U)∈W4NF。

W4NF不一定是BCNF，反之亦然。

 

cr by:《数据库系统》课程    战德臣老师（哈尔滨工业大学）