算法概括

算法的特征

1. 有穷性

   ​ 一个算法的执行必须是有终点的执行，不能无限的执行下去，这样的算法无意义

2. 确定性

   在同一个算法中输入相同的内容，输出的结果是确定的，无论输入多少次都是一样

3. 可行性

   算法必须满足实际的需求

4. 输入，输出

   算法的设计要求

   1. 正确性

   2. 可读性

   3. 健行性

   4. 高效率低储存量

      算法的度量方法

      事前分析估算法

      事前分析估算法：在程序编写的前，依据统计方法对算法进行估算

      一个算法的好坏取决于程序运行的时间和输入数据的规模

函数的渐近增长

一个算法中使用操作数来表示算法的时间复杂度。但是时间算法的复杂度受到输入数据的规模限制

如：一个操作数为 2n+3的算法与一个操作数3n+1的操作数进行比较

​ 从表中可以看出，当 n < 2时，使用3n+1的算法是最优的，但是当 n > 2时， 显然2n+3的算法使用的操作数更少，所以在使用 n>2 的数据规模时，使用A算法

函数的渐近增长：给定两个函数 f(n) 和 g(N), 如果存在一个整数N，使得n>N，f(n)>g(N),那么称f(n)的增长渐近快于g（N）

同时，在表格中也可以看出，一个操作数的常数项不影响一个操作数的大小比较，于是，一个操作数中的常数项可以忽略不计

再如：算法C的操作数;4n+8 算法D的操作数：2n²+1的比较

这个表中同样能够得出，2n²+1的线性增长大于4n+8。

同时，在这个表中可以看出，函数的常数项和最高项不影响函数的比较。所以可以忽略。

时间复杂度

衡量一个算法的优劣常常使用时间复杂来度量

时间 复杂度的定义:算法的时间复杂度是一个函数，它定性描述该算法的运行时间

时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数

时间复杂度使用大O表示法表示，常见的时间复杂度 O(1) 常数阶 O(n) 线性阶 O(n²)平方阶

推导大O阶方法

推导大O阶

1.用常数1取代运行时间中的所有加法常数

2.在修改运行次数函数中，只保留最高阶项

3.**如果最高阶项存在且不是1，则去除这个项的系数得到的就是大O表示 **

常数阶O(1)

在执行一条语句的时候，如果是赋值，变量创建，四则运算等执行恒定时间的算法都为1。但是如果执行多条O(1)的语句的时候，无论执行多少条，统一默认O(1)。

i = 0 ## 执行一次
sum = (1 + i) * n / 2 ## 执行一次
print(sum) ## 执行一次

此时的时间复杂度不是O（3）而是O(1)，因为在看到O(3)的时候先将他化成O(1)，之后因为没有最高阶，所以保留1，即最终的为O(1)

不论使用多少行的O(1)代码，最后总的时间复杂度依然为O(1)

对于分支语句而言（不包括循环语句）的时间复杂度也是O(1)

线性阶O(n)

在分析时间复杂度的时候关键要看循环语句的算法运行情况

如：

int i = 0; // 执行一次
for(i = 0;i < n;i++) // 执行N次
{
    //执行O(1)的代码
}

在这段代码中，循环语句一共循环了n次，循环体中的代码被执行了n次，所以时间复杂度为 n * O(1)

即最后的时间复杂度为O(n)。

对数阶（logn）

执行下列代码的时间复杂度是多少？

int count =1;
while(count < n)
{
    count *= 2;
    //时间复杂度为O(1)的操作代码
}

对于这段代码而言，每次执行循环体中的代码，该count就增加2倍，离n也就进了两倍，所以时间复杂度为

2^x = n，x = logn。所以该循环体中的时间复杂度为O(logn)。

平方阶O(n²)

我们已经知道以下循环的时间复杂度是O(N)

for(int i = 0;i < n; i++)
{
    //时间复杂度为O(1)的程序
}

但是如果一个循环中进行循环的嵌套，那么这个算法的时间复杂度能够成为O(n²)

如以下代码：

for(int i = 0; i < n;i++)
{
    for(int y = 0;y < n;y++)
    {
        //时间复杂度为O(1)的程序
    }
}

在这个代码中，外面循环体的时间复杂度为O(n),里面循环体中的时间复杂度为O(n)，所以总的时间复杂度为

N * N = O(n²)

但是如果改写上述代码如下;

for(int i = 0; i < n;i++)
{
    for(int y =0;y < m;y++) // 注意此时的y小于m
    {
        //时间复杂度为O(1)的代码
    }
}

上述代码中的内循环的时间复杂度为O(m) 所以总的时间复杂度为 n * m ,所以时间复杂度为O(n * m)

在观察下列代码，求时间复杂度

int x,y;
for(i = 0;i < n;i++)
{
    for( y = i;y < n;y++)
    {
        //时间复杂度为O(1)的代码
    }
}

由于当i = 0时，内循环执行了N次，当n=1时内循环执行了n-1次……当i = n-1时，内循环执行了一次，所以总的时间复杂度为
$n+（n-1）+（n-2）+……+ 1 = n(n+1)/2 = n²/2 + n/2$
采用bigO推导，去除低阶项以及高阶项系数后得到的结果为：O（n²）

如果执行函数调用时，也要计算函数体中的函数时间复杂度，最后在加上主函数中的时间复杂度，依据bigo推导得到最终的结果。

常见时间复杂度

时间复杂度大小的排序：

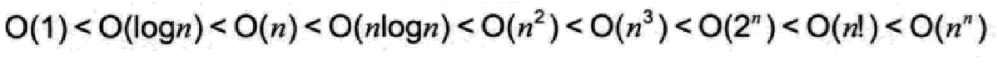
最坏情况和平均情况

最坏情况是在执行到算法最糟糕的情况，是该算法中的时间复杂度最大值。通常我们除非指定，否则所提到的运行时间都表示最坏情况的运行时间

平均期望是最有意义的情况，他是期望中的运行时间

算法空间复杂度

空间复杂度是由系统给我们分配空间的大小所决定的，如果所需要的辅助空间是一个常数，那么这个空间复杂度用O(1)表示。一般只讨论运行的时间复杂度，暂时不涉及空间复杂度。