Good Bye 2024: 2025 is NEAR Resourceful Caterpillar Sequence

题目链接

https://codeforces.com/contest/2053/problem/E

思路

• 首先肯定要确定先怎么才能让\(Aron\)赢，分成两种情况。

• 一种是\(Aron\)在叶子上了，并且\(Nora\)不在叶子上直接就赢了。

• 另一种是先\(Nora\)走一步，并且这一步无论怎么走都走不到叶子。

• 然后此时因为毛毛虫长度不变，这一步还会拉扯到尾部走到一个距离叶子为\(1\)的点。

• 剩下的都在叶子或者是拉扯完尾巴距离叶子\(>1\)这种可以一直拉来拉去都是平局。

• 第一部分非常好算，维护一下\(dp[i]\)为\(i\)节点到最近的叶子节点的距离，贡献就是距离为\(0\)的乘距离不为\(0\)的。

• 然后这个\(dp\)维护的话就是先找到一个叶子做根，然后\(dfs\)更新的话就是

• 从自己儿子到叶子距离\(dp[son]。 dp[i]=min(dp[i],dp[son]+1);\)

• 还有到根的距离\((\small因为选了叶子做根)\) \(depth[i]。dp[i]=min(dp[i],depth[i]);\)

• 第二部分，则要枚举尾巴，尾巴因为头动时会向相邻的节点移动。所以还要选个邻居，作为移动后的点。

• 这部分刚好是树所以直接\(dfs\)的时候枚举节点和节点的父亲作为初始点和移动后的点就能不重不漏了。

• 1.然后如果是把自己当成初始点，把父结点当成移动后的点，你要满足的条件就是：

• 父亲节点的\(dp[f]=1\)，然后选头的话,头的\(dp[i]>=2\)且移动的时候会让\(s->f\)。

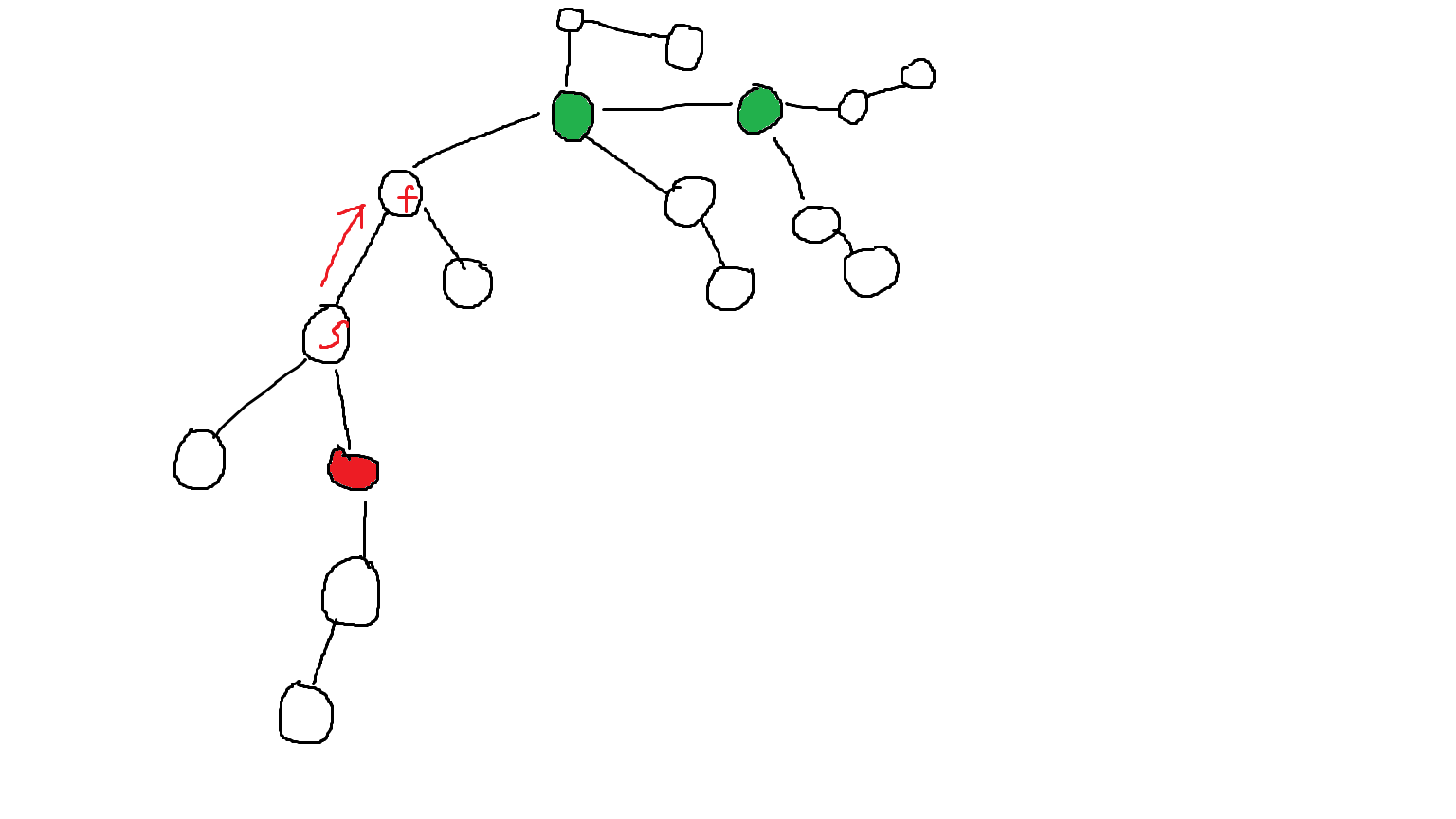
• 这个丑的要命的图就将就看看吧，绿色点就是可以做头的点。红色点虽然\(dp[i]>=2\)但移动方向不对。

• 由此看出我的贡献就是子树外\(dp[i]>=2\)的点的个数。
  

• 然后这时候可能还有个疑问\(dp[i]\)是无障碍到最近叶子的距离，但毛毛虫的身体会堵住一部分路。

• 这时候我要到叶子点的走的距离就要比\(dp[i]\)大了。

• 比如说\(dp[i]=1\)，我到叶子的距离就可能大于\(1\)。但这时候发现只有头在叶子上才能堵住路，而这部分点是\(dp[i]=0\)。

• 我统计的是\(dp[i]>=2\)的点的个数，所以一定不会堵路。

• \(dp[i]=1\)就一定是满足到叶子距离为\(1\)。

• 然后对于\(dp[i]>=2\)的点时，你距离更远了我的统计个数也不变，因为就是统计\(dp[i]>=2\)的点。

• 2.然后如果是把父亲当成初始点，把自己当成移动后的点。满足条件的就是红色点，不满足的就是绿色点。

• 贡献就是子树里\(dp[i]>=2\)的点。
  

• 维护子树里\(dp[i]>=2\)就是\(nm[i]+=nm[son];\)。

• 然后如果自己是\(dp[i]>=2，nm[i]++;\)

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=210000;
int head[N];
int nexxt[N<<1];
int to[N<<1];
int cnt=1;
int dp[N];
int depth[N];
int p=0;//整棵树上dp[i]>=2的点个数
int nm[N];//子树i里dp[i]>=2的点有多少个
int ans=0;
int f[N];//距离大于等于i的点的个数
int dg[N];//度数
void ege(int a,int b){
    to[cnt]=b;
    nexxt[cnt]=head[a];
    head[a]=cnt++;
}
void dfs1(int s,int f){
    int son=INT_MAX;
    for(int i=head[s];i;i=nexxt[i]){
        int nt=to[i];
        if(nt==f)continue;
        depth[nt]=depth[s]+1;
        dfs1(nt,s);
        son=min(son,dp[nt]);
    }
    if(son==INT_MAX)dp[s]=0;
    else dp[s]=min(son+1,depth[s]);
}
void dfs2(int s,int f){
    nm[s]=0;
    for(int i=head[s];i;i=nexxt[i]){
        int nt=to[i];
        if(nt==f)continue;
        dfs2(nt,s);
        nm[s]+=nm[nt];
    }
    if(dp[s]>=2)nm[s]++;
    if(dp[f]==1&&dp[s]!=0){
        ans+=(p-nm[s]);
    }
    if(dp[s]==1&&dp[f]!=0){
        ans+=nm[s];
    }
}
void init(int n){
    for(int i=0;i<=n;i++){
        depth[i]=dp[i]=head[i]=dg[i]=f[i]=0;
    }cnt=1;p=0;ans=0;
}
void solve(){
    int n;cin>>n;init(n);
    for(int i=1;i<n;i++){
        int a,b;cin>>a>>b;
        ege(a,b);ege(b,a);
        dg[a]++;dg[b]++;
    }
    int root=1;
    for(int i=1;i<=n;i++){
        if(dg[i]==1){
            root=i;
        }
    }
    dfs1(root,0);
    for(int i=1;i<=n;i++)f[dp[i]]++;
    f[n+1]=0;
    for(int i=n;i>=0;i--)f[i]+=f[i+1];
    ans+=(f[0]-f[1])*f[1];
    p=f[2];
    dfs2(root,0);
    cout<<ans<<endl;
}
signed main(){
#ifdef ONLINE_JUDGE
#else
    freopen("in.in","r",stdin);
    freopen("out.out","w",stdout);
#endif
    ios::sync_with_stdio(false);cin.tie(0);
    int T;cin>>T;
    while(T--){
        solve();
    }
}