大模型- 参数微调PEFT之OFT-94
参考
https://huggingface.co/docs/peft/en/conceptual_guides/oft?utm_source=chatgpt.com
https://g.co/gemini/share/dcf6b4469b35
https://arxiv.org/abs/2306.07280?utm_source=chatgpt.com
探讨一下OFT(Orthogonal Finetuning)这种参数高效微调(Parameter-Efficient Fine-Tuning, PEFT)的方法,并将其与广为人知的LoRA(Low-Rank Adaptation)进行详细的比较。
简单回顾一下为什么需要PEFT?
像GPT-3、LLaMA等大规模预训练模型,参数量动辄数十亿甚至上千亿。如果对整个模型进行全量微调(Full Fine-tuning),不仅需要巨大的计算资源(GPU显存),而且会为每个下游任务都保存一份完整的模型副本,存储成本极高。
PEFT的目标就是冻结预训练模型的大部分参数,只通过训练一小部分新增的或者选择性的参数来适应新的任务。这样既能显著降低计算和存储开销,又能达到接近全量微調的效果。LoRA和OFT就是PEFT家族中两种非常有代表性的方法。
LoRA (Low-Rank Adaptation)
LoRA是目前应用最广泛的PEFT方法之一,它的核心思想是加性低秩更新。
LoRA假设预训练模型的权重矩阵 W 是满秩的,但在适应新任务时,权重的更新量 ΔW 可以用一个低秩矩阵来近似。也就是说,模型在微调过程中的主要变化发生在一些关键的、低维的子空间中。
对于一个预训练的权重矩阵 W0,LoRA不对 W0 本身进行更新,而是通过增加一个低秩矩阵 ΔW 来进行微调。这个更新量被分解为两个更小的矩阵的乘积:
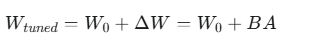
 是两个可训练的低秩矩阵。
是两个可训练的低秩矩阵。
r 是所谓的“秩”(rank),是一个远小于 d 和 k 的超参数。通常 r 的取值很小,比如8, 16, 32等。
在训练时,我们只更新矩阵 A 和 B 的参数。由于 r 很小,需要训练的参数量从 d×k 急剧下降到 r×(d+k),从而实现了参数的高效性。
前向传播时,模型的计算变为:

先计算 Ax,再计算 B(Ax),然后与原始的 W0*x 相加。这种加性结构使得在推理时,可以将训练好的 BA 直接加到 W0上,形成一个新的权重矩阵 W_tuned ,而不需要额外的计算开销。
OFT (Orthogonal Finetuning)
OFT是一种较新的PEFT方法,它另辟蹊径,采用了乘性正交更新的思路
OFT的出发点是为了在微调过程中更好地保持预训练模型的知识,避免“灾难性遗忘”。研究发现,预训练模型中权重的方向(或者说神经元之间的角度关系)对于模型的语义表达能力至关重要。
方向的改变就能学到新的知识,
OFT通过引入一个正交矩阵 R 来旋转(rotate)原始的权重矩阵 W,而不是像LoRA那样在上面添加一个增量。
正交变换是一种保持向量长度和向量间夹角的线性变换。
通过正交矩阵对权重进行变换,可以在保持模型内部结构稳定性的前提下,适应新的任务。这种方法被证明可以保持“超球面能量”(hyperspherical energy),这对于保留模型的语义生成能力至关重要。
数学原理
对于一个预训练的权重矩阵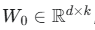 OFT通过一个正交矩阵
OFT通过一个正交矩阵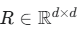 来对其进行微调:
来对其进行微调:
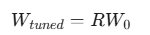
这里的关键在于 R 是一个正交矩阵,即它满足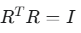 (I是单位矩阵)
(I是单位矩阵)
直接优化一个完整的正交矩阵 R 的参数量会非常大(d×d),为了实现参数高效,OFT并不直接训练一个完整的 R,而是通过其Cayley变换或其他参数化方法来构造 R
一个常见的方法是,R 可以由一个反对称矩阵 S(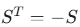 )通过Cayley变换得到:
)通过Cayley变换得到:
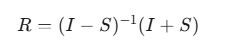
这样,我们只需要训练反对称矩阵 S 即可。
然而,即使是 S,参数量依然较大。为了进一步提升效率,OFT采用了分块对角(block-diagonal)的结构。它将权重矩阵 W 的输入维度 d 分成若干个块(block),并为每个块学习一个小的正交变换矩阵。
假设我们将 d 维空间划分为 m 个块,每个块的大小为 d/m。那么,正交矩阵 R 就会是一个分块对角矩阵:
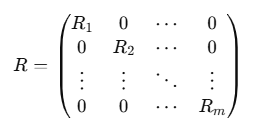
这是一个分块对角矩阵(block-diagonal matrix),对角线上是子矩阵R_1,...,R_m其它位置都是零。
每个 都是一个小的正交矩阵,
都是一个小的正交矩阵,
需要学习的参数量就从 d^2 大幅减少到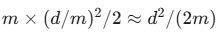
详细比较:

总结
为了更直观地理解,我们可以做一个简单的类比:
LoRA 像是在一张画上添加新的笔触。你保留了原作(W_0),但在上面添加了一些新的、低复杂度的内容(BA),使得画作呈现出新的风格或主题。
OFT 则像是在调整整张画的视角或色调。你没有添加新的内容,而是对整个画作进行了一个整体的、保持内部结构关系的变换(旋转 R),让它从一个新的角度展现出来。
应该如何选择?
如果你的任务需要模型学习与预训练任务差异较大的新知识,或者你更看重实现的简便性和广泛的社区支持,LoRA 是一个非常优秀且可靠的选择。
如果你的任务对保持预训练模型的原始能力有很高的要求,比如你只是想微调模型的风格,而不希望其语言或推理能力下降,那么 OFT 可能是一个更优的选择,因为它能更好地保护模型的“知识结构”。
正交矩阵的特性
系统地复习一下正交矩阵(Orthogonal Matrix)的特性。这是一个线性代数中非常重要的概念,理解它对于掌握像OFT这样的算法至关重要。
一个 n×n 的实数方阵 Q 如果满足以下等价条件之一,就被称为正交矩阵:
矩阵的转置等于其逆矩阵:

矩阵乘以其转置等于单位矩阵:

矩阵的列向量构成一组标准正交基(Orthonormal Basis):
- 正交性 (Orthogonal):任意两个不同的列向量的点积(内积)为 0
- 标准化 (Normal):每个列向量自身的点积为 1(即向量的L2范数或长度为 1)。
矩阵的行向量也构成一组标准正交基。
核心特性与几何解释
正交矩阵最重要的特性在于它所代表的线性变换保持了空间的几何结构。具体来说,它是一种保距变换(Isometry)。
保持向量的长度(范数)
1.对任意向量 x,经过正交矩阵 Q 变换后,其长度不变。

几何解释:变换不会拉伸或压缩任何向量。
2.保持向量间的点积(内积)
对任意两个向量 x 和 y,它们经过 Q 变换后的点积与原始点积相同。

几何解释:因为点积 x⋅y=∥x∥∥y∥cosθ,并且向量长度 ∥x∥ 和 ∥y∥ 保持不变,所以这意味着向量 x 和 y 之间的夹角 θ 也保持不变。
3.行列式的值为 ±1
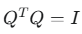
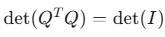
利用行列式的性质

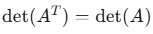
得到:
det(Q)=1 或 det(Q)=−1。
几何解释:
det(Q)=1:变换是旋转(Rotation)。它保持了空间的“手性”或“定向”(orientation)。例如,在三维空间中,它不会把你的左手坐标系变成右手坐标系。
det(Q)=−1:变换是瑕旋转(Improper Rotation),通常可以理解为反射(Reflection)或者旋转与反射的复合。它会翻转空间的“定向”。
理解这个需要理解,空间中弹簧的螺旋方向,
4,正交矩阵的乘积仍是正交矩阵
如果 Q1和 Q2都是正交矩阵,那么它们的乘积 Q1*Q2也是一个正交矩阵。
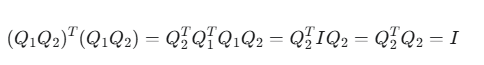
几何解释:连续进行两次不改变形状和大小的变换(如两次旋转,或一次旋转加一次反射),其最终结果仍然是一个不改变形状和大小的变换。
5,正交矩阵的逆(即转置)也是正交矩阵
如果 Q 是正交的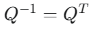
Q^T也是正交的
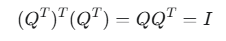
- 特征值的模长为 1
正交矩阵的(复数)特征值 λ 的绝对值(模长)总是 1,即 ∣λ∣=1。
举例
考虑一个将向量在二维平面上逆时针旋转 θ 角度的矩阵:
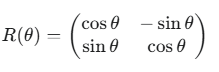
验证它的正交性:

列向量间的正交性:

行列式
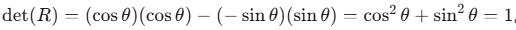
行列式为 +1,符合它是一个纯旋转的几何意义。
总结:

当你回过头看OFT时,就能更好地理解它为什么选择用正交矩阵 R 去乘以权重 W0。OFT的意图就是对原始的权重特征空间进行一次“旋转”,调整其方向以适应新任务,但同时又最大程度地保留了原始权重矩阵内部的结构信息(长度和角度关系),从而有效防止了灾难性遗忘。
看这个图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号