图像生成-FUDUKI解读-FODUKI 推理 -19
参考
https://arxiv.org/pdf/2505.20147

终于来到了FUDOKI论文的最后一站——推理(Inference)部分。这部分内容将告诉我们,在模型已经训练好之后,我们如何利用它来从无到有地生成全新的内容(比如图片或文本)
这个过程就是我们将理论付诸实践,见证“奇迹”的时刻。
宏观目标:模拟“流动”过程
推理的目标非常明确:我们要从一个\(t=0\)时的完全随机的噪声\(x₀\)出发,通过模拟我们学到的那个离散流动过程(即CTMC),一步步地、迭代地更新我们的序列,直到\(t=1\)时,得到一个清晰、高质量的最终结果\(x₁\)。
原文解读:论文提到,他们使用欧拉法(Euler solver)来模拟这个过程。这意味着我们会把t从0到1切分成许多个微小的时间步\(h\)(或者叫\(Δt\)),然后一步一步地前进。
微观操作:一个Token的“决策之旅”
现在,我们聚焦于在任何一个时间步,从 \(x_t\) 到 \(x_{t+h}\),模型是如何更新序列中的某一个Token的。
我们可以把这个过程想象成一个“角色扮演游戏(RPG)”,序列中的每一个Token都是一个正在做决策的角色。以下是角色i(即第i个Token)在一个时间步内的决策流程:
第一步:预测“最终命运” x₁^i
\(Sample x₁^i ~ p_θ^t(· | x_t) from our model\);
操作:在做任何移动之前,模型首先会审视当前的全局状态x_t(整个序列),然后对第i个位置的“最终形态”做一个整体的、全面的预测。这个预测结果x₁^i就是模型认为在t=1时,这个位置上最应该出现的那个Token。
比喻:我们的角色i在一个岔路口x_t^i,他没有立刻决定下一步往哪走,而是先拿出地图,根据周围所有的环境线索x_t,推算了一下自己的最终目的地应该是哪里。比如,他推断出:“哦,我最终要去的地方应该是‘熊猫’这个词”。
第二步:计算“离开的冲动” λ^i
\(Compute the total conditional transition rate λ^i = Σ u_t(...)\)
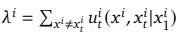
操作:在预测出最终目的地\(x₁^i\)之后,模型会用我们熟悉的条件向量场\(u_t(x^i, z^i | x₁^i)\)来计算,从当前状态\(x_t^i\)出发,流向所有其他可能状态\(x^i\)的总速率之和。
比喻:角色i知道了自己的最终目的地是“熊猫”后,他开始评估自己当前的处境。这个\(λ^i\)(lambda)就代表了他离开当前位置的“总冲动”或“不安分程度”。
如果当前位置很差,有很多更好的选择能让他更快地接近“熊猫”,那么他的“离开冲动”\(λ^i\)就会很高。
如果他当前的位置已经很不错了,没什么更好的选择,那么\(λ^i\)就会很低。
第三步:抛硬币/掷骰子 \(Z_change\)
\(Draw a uniform random variable Z_change ~ U[0, 1]\)
操作:从0到1之间随机取一个数。
比喻:角色\(i\)现在要通过一个随机事件,来决定是否要将“离开的冲动”付诸行动。
第四步:决策:跳跃还是停留?
这是最关键的决策步骤。角色i会将他的“随机数”\(Z_change\)与一个阈值进行比较。
阈值:\(1 - e^(-hλ^i)\)
这个阈值是什么? 这是源于CTMC理论的一个标准公式,它代表在“离开冲动”为\(λ^i\)的情况下,在一段极短的时间h内,角色\(i\)决定“跳跃”的概率。
\(λ^i\)(冲动)越大,这个概率就越接近1。
\(λ^i\)(冲动)越小,这个概率就越接近0。
如果 \(Z_change ≤ 1 - e^(-hλ^i)\) (随机数小于等于跳跃概率)
决策:跳跃 (Jump)!
跳向哪里? 角色不会随便乱跳,他会从一个新的概率分布 \(u_t(...) / λ^i\) 中采样一个新的状态\(x_{t+h}^i\)。
这个新分布是什么? 它是一个归一化的“流动方向”分布。简单来说,角色i会优先选择跳向那个\(u_t\)(速度)指向最强的方向。这保证了跳跃是智能的,是朝着模型认为最优的方向进行的。
如果 \(Z_change > 1 - e^(-hλ^i)\) (随机数大于跳跃概率)
决策:停留 (Stay)!
操作:\(x_{t+h}^i = x_t^i\)。角色决定这一步待在原地不动,观察一下情况。
总结
推理步骤,完美地体现了FUDOKI相比于传统“完形填空”式模型的优势:
全局引导:每一步的决策,都是在模型对全局最终状态进行一次预测的指导下进行的,而不是只看局部。
动态修正:Token的状态不是一次性决定的。一个Token在这一步可能“跳跃”到了“熊猫”,但在下一步,模型可能会根据更新后的上下文,再次产生巨大的“离开冲动”,并“跳跃”到更合适的“红熊猫”。
概率性与智能性结合:“跳不跳”是一个概率性事件,这增加了生成的多样性;而“往哪跳”则是由模型学到的智能速度场u_t精确引导的,这保证了生成的质量。
最终,通过N次这样的迭代,一个完全随机的Token序列,就在这样不断“预测终局 -> 评估冲动 -> 概率性跳跃”的智能决策中,逐渐“流动”并“凝聚”成了我们最终看到的、清晰且高质量的图像或文本。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号