图像生成-FUDUKI解读-Metric-induced Probability Paths + Kinetic Optimal Velocities -16
参考
https://arxiv.org/pdf/2505.20147


现在进入了FUDOKI论文最核心的创新部分。前面的内容是“离散流匹配”的通用框架,而这一部分则是FUDOKI自己独创的、更高级的“配方”。
我们来详细解读F-UDOKI是如何定义其独特的“由度量引导的概率路径” (Metric-induced Probability Paths) 和 “动能最优速度” (Kinetic Optimal Velocities) 的。
Metric-induced Probability Paths
首先,我们要理解为什么要改进?
之前讨论的那个“概率混合路径” \((p_t = (1-κ_t)p_noise + κ_t*p_data)\) 虽然简单,但有一个缺点:它有点“傻”。
“传送”式的变换:在那个路径中,一个Token在t时刻,要么是完全随机的噪声,要么就瞬间变成了那个完全正确的Token。它没有一个“逐渐变得更像”的过程。比如从噪声变成单词"cat",它不会先变成发音或字形相似的"bat"或"car",而是直接从随机的"x"或"z"一步到位。
FUDOKI的作者认为,一个更理想的路径应该是“有意义的”。当目标是"cat"时,那些与"cat"在语义上或形态上相似的词(如"bat", "car")的概率也应该随之提升。这就引出了FUDOKI的新设计。
FUDOKI的路径配方:由度量引导 (Metric-induced)
FUDOKI不再使用简单的“混合”,而是定义了一条由“距离”主导的路径。

\(d(x^i, x_1^i)\) (距离函数/度量):这是新配方的灵魂。它计算任意一个Token \(x^i\) 与我们的目标Token \(x₁^i\) 之间的“距离”或“不相似度”。
这个距离通常是在一个有意义的嵌入空间(Embedding Space)中计算的。比如,单词"猫"和"狗"的嵌入向量离得很近,但和"车"的嵌入向量离得很远。
这意味着,我们的路径现在理解了Token之间的语义关系!
β_t (调度器/温度的倒数):这是一个从 \(β₀ = 0\) 单调递增到 \(β₁ = ∞\) 的“旋钮”。你可以把它想象成“引力常数”或“聚焦强度”。
新路径是如何演化的?
在 \(t=0\) 时 \((β₀=0)\):
公式变为 \(softmax(0)\)。一个全零向量的softmax结果是一个均匀分布。
含义:在旅程开始时,所有Token的概率完全相同。这是一个完美的、无偏向的“混沌”或“噪声”状态。
在 \(t=1\) 时 \((β₁=∞)\):
\(β_t\)变得无穷大。在 \(-β_t * d(...)\) 这一项中,只有当\(d=0\)(即\(x^i = x₁^i\))时,结果是\(0\);对于任何其他\(x^i\),结果都是一个巨大的负无穷。
softmax函数会将所有概率(100%)都集中在那个值为0的输入上。
含义:在旅程结束时,概率完全集中在目标Token \(x₁^i\) 上。
在 \(0 < t < 1\) 时 (旅程中):
β_t是一个有限的正数。softmax会给那些 \(-β_t * d(...)\) 更接近0(即d(...)更小)的Token赋予更高的概率。
含义:那些与目标 \(x₁^i\) “距离”更近的Token,其概率会更高。目标Token \(x₁^i\) 就像一个“引力源”,随着\(β_t\)(引力)的增强,它不仅会吸引自己,还会把它周围“空间”中相似的Token也一起“拉拢”过来,使它们的概率也随之提升。
FUDOKI的速度配方:动能最优 (Kinetic Optimal)
有了这条更智能的路径,驱动它的“速度场”u_t是什么样的呢?论文指出,这个速度场是通过最小化“动能”得到的,并给出了最终的公式。
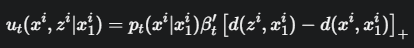
\(u_t(x^i, z^i | ...)\):代表从“源”Token \(z^i\) 流向“目标”Token \(x^i\) 的速率。
\([...]_+\):这是ReLU函数,即 \(max(0, ...)\)。
\(d(z^i, x_1^i) - d(x^i, x_1^i)\):这是整个公式的“开关”和“方向盘”。
它计算的是:从\(z^i\)移动到\(x^i\)后,我们离最终目标\(x₁^i\)的距离变化了多少。
情况一:如果新位置 \(x^i\) 比旧位置 \(z^i\) 更靠近最终目标(即 \(d(x^i,...) < d(z^i,...)\)),那么括号里的差值就是正数。ReLU函数会保持这个正值,于是允许流动。
情况二:如果新位置 \(x^i\) 比旧位置 \(z^i\) 更远离最终目标,那么差值就是负数。ReLU函数会把它变成0,于是流动速率为0,禁止流动。

这个“动能最优速度”强制规定了一个非常聪明的“下山”原则。在以\(x₁^i\)为“谷底”的“语义地形”中,概率质量只被允许从“高处”流向“低处”,绝不允许“爬山”。这确保了整个流动过程是单向的、高效地向着目标收敛的。
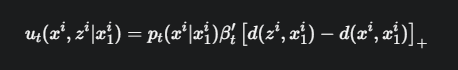
理解了最关键的“下山”原则 [...] 部分,现在我们来详细解释另外两个同样重要的乘法项:\(p_t(x^i | x_1^i)\) 和 \(β'_t\)。

这个公式描述的 \(u_t\) 是从“源”Token \(z^i\) 流向“目标”Token \(x^i\) 的速率。这个速率的大小,是由三个因子相乘共同决定的。
因子A:\([...]_+\) —— 方向的“开关”
方向控制器 (Direction Controller) 或 合法性开关 (Validity Switch)。
这是我们已经理解的部分。它负责判断这次“流动”是否被允许。
规则:
只有当目标 \(x^i\) 比源 \(z^i\) 更接近最终目的地 \(x₁^i\) 时,这个开关才是“ON”(值为正)。
否则,开关就是“OFF”(值为0),整个流动速率 \(u_t\) 直接变为0,流动被禁止。
一句话总结:它确保了概率流动永远是“向下游”或“下山”的,从不倒流。
因子B:\(β'_t\) —— 全局的“节拍器”
角色:全局速率控制器 (Global Speed Controller) 或 时间节拍器 (Timetable)。
解释:
我们知道 \(β_t\) 是一个从\(0\)到\(∞\)变化的调度函数,它控制着整个过程的“聚焦强度”。
\(β'_t\) 则是这个调度函数 \(β_t\) 对时间的导数,代表了\(β_t\)的变化速率。
直观理解:\(β'_t\) 设定了在 t 这个特定时刻,整个系统“演化”的总体剧烈程度或紧迫感。
如果在一个时间段内 \(β_t\) 增长得很快,那么 \(β'_t\) 就很大,意味着此刻的流动应该非常迅速和剧烈。
如果 \(β_t\) 增长得很慢,那么 \(β'_t\) 就很小,意味着此刻的流动是平缓和温和的。
比喻:想象一场交响乐。\(β_t\) 是乐谱的进程,而 \(β'_t\) 是指挥的指挥棒挥舞的幅度。在乐曲的高潮部分,指挥棒挥舞得又快又猛(\(β'_t\)值大),所有乐器(流动)都变得激昂;在舒缓的段落,指挥棒轻柔缓慢(\(β'_t\)值小),所有乐器都变得柔和。
因子C:\(p_t(x^i | x_1^i)\) —— 资源的“引导器”
角色:目标概率权重 (Target Probability Weight) 或 资源引导器 (Resource Guide)。
解释:
\(p_t(x^i | x_1^i)\) 是在t时刻,目标位置 \(x^i\) 本身的概率密度。
它代表了在当前时刻,\(x^i\) 这个状态的“合理性”或“ plausibility”。
直观理解:一个流动过程不仅要有方向和速度,还要有明确的目的地。这个因子的作用,就是让概率质量优先流向那些在当前时刻更“合理”、更“应该”出现的状态。
比喻:想象我们正在从一个大水池(源 \(z^i\))向许多小杯子(不同的目标 \(x^i\))注水。
开关 \([...]\) 决定了哪些杯子(更近的)可以被注水。
节拍器 \(β'_t\) 决定了水流的总阀门开多大。
而这个 \(p_t\) 因子,则是在每个可注水的杯子前又加了一个独立的阀门。在 \(t\) 时刻越重要、越应该被充满的杯子,它的阀门就开得越大,流向它的水流速率就越高。那些虽然路径正确但不太重要的杯子,流向它的水流就会被减弱。
现在我们把三个因子串联起来,理解完整的流动速率 \(u_t\):
一场大规模的城市疏散,目标是市民中心 \(x₁^i\)
规则(因子A):所有交通必须沿着能更接近市民中心的道路行驶,任何绕远路的行为都会被立刻阻止(\([...]\)开关)。
指令(因子B):城市应急广播(\(β'_t\))在不同时间下达不同的指令。比如,“9点-10点,请有序疏散”;“10点-11点,请全速前进!”。这决定了整个城市交通的总体节奏。
调度(因子C):交通控制中心(\(p_t\))会根据实时情况,优先将车流引导向那些在当前阶段最关键、最合理的中间集结点 x^i。即便一条路符合“更接近”的规则,但如果它通向一个偏僻的、非计划内的区域,通往那里的绿灯时间就会很短(\(p_t\)值小),流量就会受限。
因此,这个看似复杂的公式,实际上描述了一个非常有组织、有纪律、有目标的流动过程。它确保了概率的流动方向正确、节奏可控,并且总是优先流向最合理的目标,从而高效、稳定地完成从噪声到数据的转化。
总结
FUDOKI的这一部分,是对基础Flow Matching框架的一次重大升级:
它用一个理解语义相似性的“度量引导路径”,取代了原来简单的“随机混合路径”。
它推导出并使用了一个遵循“只许下山,不许爬山”原则的“动能最优速度场”作为学习目标。
这个更智能、更有方向感的“教师”\(u_t\),使得神经网络\(v_θ\)的学习过程更具结构性,不仅仅是在学习“是非题”(是噪声还是数据),更是在学习一个关于数据内在联系和结构的“地图”。这正是FUDOKI能够统一“理解”与“生成”任务的根本原因。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号