图像生成-Flow Matching思想-11
参考
https://gemini.google.com/app/a5a75c33b55945bd
https://zhuanlan.zhihu.com/p/685921518

这部分内容是对Flow Matching动机和核心思想的一个非常精彩的总结。它完美地衔接了我们之前讨论的所有知识点,并点明了Flow Matching的核心优势。
分为四个部分:
回顾旧方法(CNF)的痛点。
提出新方法(Flow Matching)的核心思想和公式。
点出新方法自身面临的挑战。
给出解决挑战的最终方案(Conditional Flow Matching)
CNF的“慢”—— 为什么要改进?
传统的连续归一化流(CNF)虽然强大,但无论是训练(计算似然)还是采样(生成图片),都离不开一个核心操作:求解常微分方程(ODE)。
要计算一张真实图片 \(x₁\) 的概率 \(p(x₁)\),需要从 \(x₁\) 出发,反向求解ODE一路回到 \(x₀\)。
要从一个噪声 \(x₀\) 生成一张新图片,需要从 \(x₀\) 出发,正向求解ODE一路“流”向 \(x₁\)
这个求解过程需要反复调用神经网络成百上千次,就像要模拟上千帧的动画一样,计算量巨大,过程非常缓慢。
这个需要求解的常微分方程(ODE)是一个神经网络,\(v(x_t, t)\) 模拟的是一个速度场,回答在\(x_t\)这个位置的速度
想象一位CNF雕刻家。他每想凿一刀(计算一次loss),都得先把自己未来的所有动作(整个ODE路径)在脑子里完整地模拟一遍,这太耗费精力了。
Flow Matching的核心思想 —— “无模拟训练”
Flow Matching(FM)是一种用来训练CNF的新技巧。
它是 Simulation-Free 的,即“无模拟的”。这意味着在训练过程中,我们不再需要求解那个耗时的ODE了!
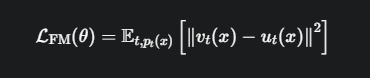
\(u_t(x)\):我们称之为目标向量场或“教师流场”。这是我们希望模型能学会的、那个“完美的”、“理想的”速度场。
\(v_t(x)\):这是我们正在训练的神经网络,即“学生模型”。
\(|| ... ||²\):计算“学生”的答案和“教师”的答案之间的差距(均方误差)。
\(E_{t, p_t(x)}[...]\):代表我们在随机的时间点 \(t\) 和随机的位置 \(x\)(该位置符合t时刻的概率分布\(p_t(x)\))上,对学生进行“抽查考试”。
训练过程的巨大转变:
CNF(旧方法):学习过程是间接的。通过最大化一个复杂的似然函数来“倒逼”模型v_t学到正确的行为,数值化的求解OED。
Flow Matching(新方法):学习过程是直接的、监督式的。我们有了一个明确的“教师”\(u_t(x)\),然后让“学生”\(v_t(x)\)去直接模仿老师的行为。
只需要在随机的(t, x)点上,计算v_t和u_t的差值即可,完全不需要知道完整的流动轨迹。
这就摆脱了对ODE求解的依赖,实现了“无模拟训练”,大大加快了训练速度。
Flow Matching自身的挑战 —— “教师”从何而来?
一个显而易见的问题。这个方法虽然直观,但它依赖于我们预先知道那个理想的“教师流场”\(u_t(x)\)和它所对应的“概率路径”\(p_t(x)\)。
但在现实中,我们恰恰不知道连接简单高斯分布和复杂数据分布的那个“理想路径”和“理想速度场”具体长什么样。
最终的解决方案 —— Conditional Flow Matching“条件流匹配”
虽然请不来那个能教所有科目的“全科王牌教师”(边际场 \(u_t(x)\))。
但是,我们可以轻松请来无数个只教一个知识点(比如“从噪声点A到真实图片点B”)的“单科专家教师”(条件场\(u_t(x|x₁)\))。因为点对点的路径和速度场非常容易定义(比如一条直线)。
然后,我们把这些“单科专家”的意见,通过一个“加权平均”的公式(我们上次讨论的带星号的公式),组合成一个无所不知的“虚拟王牌教师”(边际场 \(u_t(x)\))。
问题解决! 我们现在有了可以模仿的“教师”\(u_t(x)\),并且这个教师是通过简单、可控的方式构建出来的。
总结
出发点:CNF训练太慢,因为它依赖于ODE模拟。
核心思想:我们能不能不模拟,直接让模型v_t去模仿一个理想的“目标流场”\(u_t\)?(这就是FM的核心Loss函数)。
遇到的困难:理想的u_t我们不知道。
最终的方案:通过条件化(Conditional)的方法,从无数个简单的、点对点的理想流场 \(u_t(x|x₁)\) 出发,构建出我们需要的那个复杂的、全局的理想流场 \(u_t(x)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号