图像生成-条件概率与边际概率-10

参考

https://zhuanlan.zhihu.com/p/685921518

这部分内容是Flow Matching理论的精髓所在，它解释了如何从简单、易于构建的“点对点”路径，来定义出我们最终需要学习的、复杂的全局向量场。
看懂了这里，Flow Matching的训练方式就豁然开朗了。

问题的根源：理想与现实

在我们之前的讨论中，Flow Matching的理想是：
定义一条从简单分布 \(p₀\) 到数据分布 \(p₁\) 的“概率路径” \(p_t(x)\)。
计算出这条路径对应的“理想速度场” \(u_t(x)\)。
训练神经网络 \(v_θ\) 去模仿 \(u_t(x)\)。

但现实中的问题是：第一步就很难！
如何在 p₀（一个标准高斯分布）和 p₁（一个极其复杂、未知的、由所有猫的图片构成的分布）之间，
定义一条“简单”的路径？这在数学上非常棘手。

解决方案：化整为零，逐个击破

Flow Matching的作者提出了一个绝妙的解决方案：我们不在两个遥远而复杂的“分布”之间直接连线，而是在分布中的“点”之间连线。

第一个概念：条件概率路径

条件概率路径 (Conditional Probability Path) \(p_t(x₀ | x₁)\)
\(x₁\): 我们从真实数据集中随机抽取的一个样本。比如，一张特定的猫的照片。我们将 \(x₁\) 视为一个确定的终点。
\(x₀\): 我们从简单高斯分布中随机抽取的一个样本。这是一个确定的起点。
\(p_t(x₀ | x₁)\): 这描述了一个点对点的“旅程”。它定义了在“终点是x₁”这个条件下，一个粒子从x₀出发，在时间t时，它的概率分布是怎样的。

这个“条件路径”可以被我们人为地设计得非常简单。最简单的设计就是直线路径：
在时间t，粒子的位置就是起点和终点的线性插值： \(x_t = (1-t)x₀ + t*x₁\)。
那么，\(p_t(x₀ | x₁)\) 就可以是一个以这个x_t为均值，方差很小的高斯分布。
你看，定义一个“点到点”的简单路径，远比定义一个“分布到分布”的路径容易得多。

边际概率路径

边际概率路径 (Marginal Probability Path) \(p_t(x)\)
现在，有了成千上万条从不同噪声起点到不同真实图片终点的“点对点”路径。那么，在时间t，整个空间中的概率分布长什么样呢？

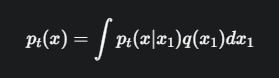
\(q(x₁)\): 真实数据 x₁ 的概率分布。
\(∫ ... dx₁\): 积分符号在这里代表“对所有可能的终点x₁进行加权平均”。

比喻：

把 \(q(x₁)\) 想象成中国所有城市的人口分布图。
每一条 \(p_t(x | x₁)\) 是从一个随机地点出发，到特定城市 \(x₁\) 的一条高速公路。
那么，边际概率路径 \(p_t(x)\) 就代表了在下午 t 点这个时刻，全国所有高速公路上所有汽车的位置分布。它是所有单一高速公路交通状况的叠加和平均。

通过这种方式，我们用无数条简单的“条件路径”，成功地构建出了一个复杂的、随时间演化的“边际路径”\(p_t(x)\)。
这个 \(p_t(x)\) 会平滑地从 \(t=0\) 时的p₀分布（所有车都在随机地点）演变到 \(t=1\) 时的\(p₁\)分布（所有车都到达了各自的目标城市）。

核心公式：边际向量场

路径的问题解决了，那么驱动路径的速度场呢？同样地，我们可以从简单的“条件速度场”构建出复杂的“边际速度场”。

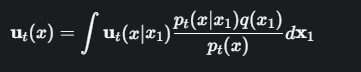
这个公式是Flow Matching的核心，我们来深入解读它：

\(u_t(x)\): 我们最终想让神经网络模仿的边际向量场。它回答了问题：“在t时刻，位于x处的任何一个粒子，它的理想速度应该是多少？”
\(u_t(x | x₁)\): 条件向量场。它回答了更简单的问题：“如果我知道我的终点是x₁，那么我在t时刻、x位置的速度应该是多少？”。对于我们上面设计的直线路径，这个速度就是恒定的 x₁ - x₀。
\(p_t(x|x_1)q(x_1) / p_t(x)\): 这是最关键的权重项。
根据贝叶斯定理，这个复杂的比值恰好等于 \(p_t(x₁ | x)\)！
\(p_t(x₁ | x)\) 的含义是：“后验概率”，它回答了这样一个问题：“我现在（t时刻）位于x点，那么我的最终目的地是x₁的概率有多大？”

现在，整个公式的含义就清晰了：
在t时刻，一个位于x点的粒子，它的理想速度 \(u_t(x)\)，是所有可能的目标速度 \(u_t(x|x₁)\) 的加权平均。
而这个平均的权重，就是它前往那个特定终点x₁的可能性 \(p_t(x₁|x)\)。

再用GPS导航比喻：
你开车到了一个复杂的交叉路口 \(x\)，你的GPS（神经网络\(v_θ\)）为了计算出最佳的前进方向 \(u_t(x)\)，它会在后台这样做：
它考虑了所有你可能要去的目的地\(（所有x₁）\)。
它计算出如果要去每个目的地，当前应该走的方向\(（u_t(x|x₁)）\)。
它根据你当前的位置 \(x\)，推断出你去每个目的地的可能性有多大（权重\(p_t(x₁|x)\)）。
最后，它把所有可能方向按照这个可能性加权平均，得出一个最合理的综合方向，告诉你该怎么走。

Theorem 1 就像是给这套复杂的流程盖上了一个“质量合格”的印章。它从数学上严格证明了：
只要你为每个“点对点”的简单路径设计的“条件速度场” \(u_t(x|x₁)\) 是正确的，那么通过上述加权平均公式得到的“边际速度场” \(u_t(x)\)，也必然是能驱动那个复杂的“边际概率路径” \(p_t(x)\) 的正确速度场。
这个定理让我们能放心地去定义简单的条件路径和条件场，因为我们知道，由它们构建出的最终目标 \(u_t(x)\) 是理论正确的。我们的神经网络只需要努力去模仿这个 \(u_t(x)\) 就行了。