图像生成-Normalizing Flows(NFs)归一化流-07

目录

• 参考
• 核心思想：橡皮泥的比喻
• 公式

参考

https://zhuanlan.zhihu.com/p/685921518
Normalizing Flows(NFs)是一种可逆的概率密度变换方法，它的核心思想是通过一系列可逆的变换函数来逐步将一个简单分布（通常是高斯分布）转换成一个复杂的目标分布，
这个过程可以被看作是一连串的变量替换的迭代过程，每次替换都遵循概率密度函数的变量变换原则。
通过这种方式，Normalizing Flows能够精确地计算出变换后的分布的概率密度，从而实现从简单分布到复杂分布的精确映射。

核心思想：橡皮泥的比喻

要理解归一化流，我们可以先不用看公式，而是想象一个简单的过程：
初始材料：你手里有一块形状非常简单、质地均匀的橡皮泥，比如一个标准立方体。这块橡皮泥，就代表一个我们非常了解的、简单的基础概率分布 \(π₀(z₀)\)，比如标准高斯分布（钟形曲线）。
变换过程：现在，你通过一系列可逆的、精巧的“揉、拉、捏、搓”的动作，把这个简单的立方体变成了一个非常复杂的形状，比如一只惟妙惟肖的“兔子”。这一系列可逆的变换动作，就是归一化流的核心 \(f₁, f₂, ..., fₖ\)。
最终成品：这只复杂的“兔子”，就代表了我们想要学习的目标概率分布 \(p(x)\)，比如所有“猫”的图片的分布。

归一化流的核心思想就是：通过一连串可逆的、可计算的函数变换 \(f\)，将一个简单的基础分布 \(π₀\) 变成一个复杂的目标分布 \(p(x)\)。
它的“超能力”在于，由于每一步变换都是可逆且精确的，我们能够精确地计算出任何一个数据点 x 的概率密度 p(x)，这是很多其他生成模型（如GAN）做不到的。

公式

是原始的简单分布（例如标准高斯分布）
Normalizing Flows希望通过一系列可逆变换 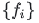将其转换成目标分布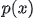，这些变换定义了从 \(z_0\) 到 \(x\) 的映射，并且每一步变换 \(f_i\) ​都有其逆变换 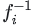。那么，变换过程可以表示为：

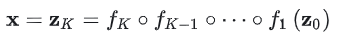
对于其中第 \(i\) 步，有：

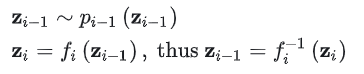
根据率密度函数的变量变换关系可得：

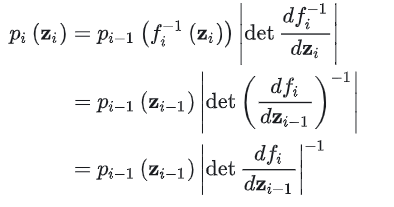
其对数似然为：

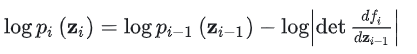
给定这样一连串的概率密度函数和变换关系，可以逐步展开直至追溯到初始分布，可得：

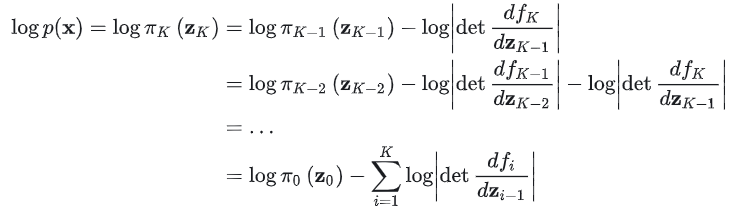
当这一系列变换函数 \(f_i\) 可逆，且雅可比矩阵易于计算，模型训练时，优化目标为负对数似然：

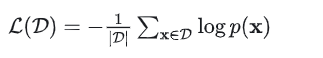
目标是让我们模型所描述的概率分布 \(p(x)\)，尽可能地贴近真实数据的分布。换句话说，对于一个从真实数据集中拿出的样本 \(x\)（比如一张真实的猫图），我们希望我们的模型认为“这张图很真实”，也就是赋予它一个尽可能高的概率 \(p(x)\)。

这个原则，在统计学上称为最大似然估计（Maximum Likelihood Estimation, MLE）。

\(log p(x)\): 这就是我们上面费了半天劲算出来的、我们的模型赋予真实数据点 x 的对数概率。我们希望这个值越大越好。
\(Σ log p(x)\): 我们把数据集中所有样本的对数概率都加起来。我们希望这个总和越大越好。
最关键的负号 \(-\)，在深度学习中，我们使用的所有优化算法（如梯度下降）都是朝着最小化（Minimize）损失函数的方向前进的。
那么，如何把一个“最大化问题”变成一个“最小化问题”呢？
非常简单，在前面加一个负号。

最大化 \(A\) 等价于 最小化 \(-A\)