图像生成-PPDM-plus-03
参考:https://zhuanlan.zhihu.com/p/614498231
模型训练
我们可以直接基于原始数据 \(X_0\) 来对任意 \(t\) 步的 \(X_t\) 进行采样,那么在实际训练过程中,我们不必将所有的时间片都拿来训练。而采取直接采样到时刻 \(t\)
然后得到该时刻的 \(X_t\) 并使用神经网络预测添加的噪声即可,因为扩散模型的 \(T\) 是一个非常大的值,使用这种方式将大幅提升训练速度。它的训练过程为:
从分布为 \(q(x_0)\) 的数据集随机采样一个样本 \(x_0 ~ q(x_0)\)
从 \(1\) 到 \(T\) 中随机采样一个值 \(t\) ,用于表示添加噪声的水平;
随机采样一个二维高斯噪音 \(\epsilon\) ,然后使用上面介绍的“Nice Property”对 \(X_0\) 施加 \(t\) 级别的噪声;
训练神经网络根据加噪之后的 \(X_t\) 预测作用到 \(X_0\) 之上的噪声。

样本生成
扩散模型的生成过程是一个反向去噪的过程,它的伪代码见算法2。具体的讲,我们从 \(T\) 时刻开始,首先随机采样一个高斯噪声。
使用神经网络预测的噪声逐渐对其去噪,直到 \(0\) 时刻停止。
从 \(X_t\) 到 \(X_{t-1}\) 的计算公式
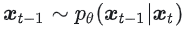
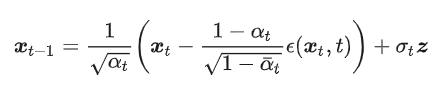
 是一个二维标准高斯分布
是一个二维标准高斯分布
算法过程:

这张截图展示的是扩散模型(具体来说是DDPM论文中)的采样算法(Sampling Algorithm),也就是我们心心念念的、从噪声生成一张全新图片的具体操作步骤。
我们来逐行解读这个“魔法”是如何发生的。
整体概览:一个雕刻家的工作流程
你可以把这个算法想象成一位雕刻家,他的任务是从一块充满随机纹理的大理石(纯噪声)中雕刻出一座精美的雕像(清晰图片)。
第1行:雕刻家拿到一块原始的大理石 \(x_T\)。
第2行:雕刻家准备开始工作,总共需要精雕细琢 \(T\) 次(比如1000次)。
第3-4行:每一次,他都会用他神奇的工具(神经网络)鑿掉一些“废料”(噪声),让雕像的轮廓更清晰一点。
第6行:经过 \(T\) 次精雕细琢后,一块完美的作品 \(x_0\) 诞生。
第1行: \(x_T ~ N(0, I)\)
含义:初始化。我们从一个完全随机的图像 \(x_T\) 开始。这个图像是从一个标准高斯分布(均值为0,方差为1)中采样得到的。
大白话:我们先创建一张和目标图片尺寸相同的“画布”,但上面画满的不是白色,而是毫无规律、五彩斑斓的电视雪花噪声。这就是我们雕刻的原材料。
第2行: \(for t = T, ..., 1 do\)
含义:这是一个倒序循环。我们从最后一步 \(t=T\) 开始,一步步往前推,直到 \(t=1\)。
大白话:我们的雕刻工作从最粗糙的状态开始,一步步精细化。
第4行: \(x_{t-1} = ...\) (核心公式)
这是整个算法的灵魂,也是最复杂的一行。它告诉我们如何从当前步骤的图片 \(x_t\),计算出上一步稍微清晰一点的图片 \(x_{t-1}\)。
我们可以把这个公式拆成两个主要部分来理解:

部分一:基于预测的确定性去噪(The Denoised Part)
这部分是去噪的主力。
\(ε_θ(x_t, t)\):这是最核心的组件。我们的U-Net神经网络上场了!它接收当前的噪声图片 \(x_t\) 和当前的时间步 \(t\) 作为输入,然后输出它预测出的噪声 \(ε\)。
\(x_t - ... * ε_θ(...)\):这里的核心思想是“从当前图片中减去预测出的噪声”。虽然前面有一个复杂的系数 \((1-α_t)/√(1-ᾱ_t)\),但你只需要理解,它的作用是根据当前的时间步 \(t\) 来正确地缩放我们预测出的噪声,以确保数学上的正确性。
\(1/√α_t * (...)\):对减去了噪声的结果再进行一次缩放。
关键洞察:这复杂的第一部分,其实就是在计算我们之前在“逆向过程”中提到的那个理论后验分布的均值 \(μ̃_t\)。它代表了模型根据当前情况,能给出的对上一步 \(x_{t-1}\) 的“最佳猜测”。
部分二:添加一点可控的随机性(The Random Part)
\(z\):来自第3行 \(z ~ N(0, I)\)。在每一步(除了最后一步 \(t=1\)),我们都会生成一个新的、标准的高斯噪声。
\(σ_t\): 这是一个与 \(t\) 相关的系数,代表了我们要添加的这部分新噪声的强度(标准差)。这个值通常很小,并且也是根据 \(β_t\) 预先计算好的。
为什么去噪还要再加噪声?
这是因为逆向过程本身也是一个概率性的马尔可夫链,而不是一个完全确定的过程。加入这一丁点儿新的随机性,有两大好处:
提高生成样本的多样性:确保每次从同一个 \(x_t\) 出发,得到的 \(x_{t-1}\) 都有微小的不同。
修正模型的错误:如果模型在某一步的预测有偏差,这点随机性可以帮助它“跳出”错误的轨迹,增加生成过程的鲁棒性。
第6行: \(return x_0\)
含义:当循环从 \(t=T\) 一路运行到 \(t=1\) 后,我们最终得到了 \(x_0\)。
大白话:经过1000次(或T次)的“预测噪声 -> 减去噪声 -> 添加微小随机性”的迭代后,最初那张完全随机的雪花图,已经被“雕刻”成了一张清晰、真实、且全新的图片。这就是我们最终的作品。
总结
DDPM作为一个扩散模型的基石算法,它有着很多早期算法的共同问题:
采样速度慢:DDPM的去噪是从时刻T到时刻1的一个完整的马尔可夫链的计算,尤其是DDPM还需要一个比较大的T才能保证比较好的效果,这就导致了DDPM的采样过程注定是非常慢的;
生成效果差:DDPM的效果并不能说是非常好,尤其是对于高分辨率图像的生成。这一方面是因为它的计算速度限制了它扩展到更大的模型;另一方面它的设计还有一些问题,例如逐像素的计算损失并使用相同权值而忽略图像中的主体并不是非常好的策略。
内容不可控:我们可以看出,DDPM生成的内容完全还是取决于它的训练集。它并没有引入一些先验条件,因此并不能通过控制图像中的细节来生成我们制定的内容。
pytorch实现
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import os
def get_beta_schedule(T, beta_start=1e-4, beta_end=0.02):
return torch.linspace(beta_start, beta_end, T)
class Diffusion:
def __init__(self, T=1000, device='cuda'):
self.T = T
self.device = device
self.betas = get_beta_schedule(T).to(device)
self.alphas = 1. - self.betas
self.alphas_bars = torch.cumprod(self.alphas, dim=0)
def q_sample(self, x0, t, noise=None):
if noise is None:
noise = torch.randn_like(x0)
# t: (B,) - x0: (B, C, H, W)
# self.alphas_bars: (T,)
# We want to gather the correct alpha_bar for each batch element
# Output: (B, 1, 1, 1)
sqrt_alph_bar = torch.sqrt(self.alphas_bars[t]).view(-1, 1, 1, 1)
sqrt_one_minus_alph_bar = torch.sqrt(1 - self.alphas_bars[t]).view(-1, 1, 1, 1)
return sqrt_alph_bar * x0 + sqrt_one_minus_alph_bar * noise
# UNet-like 架构(简化版)
class SimpleDenoiseNet(nn.Module):
def __init__(self, img_channels=1):
super().__init__()
# Only support 2D images (B, C, H, W) for Conv2d
self.net = nn.Sequential(
nn.Conv2d(img_channels + 1, 64, 3, padding=1),
nn.ReLU(),
nn.Conv2d(64, 128, 3, padding=1),
nn.ReLU(),
nn.Conv2d(128, 128, 3, padding=1),
nn.ReLU(),
nn.Conv2d(128, img_channels, 3, padding=1),
)
def forward(self, x, t):
# Accept (B, C, H, W) only
if x.dim() != 4:
raise ValueError(f"Input to SimpleDenoiseNet must be 4D (B, C, H, W), got {x.shape}")
# t: (B,) -> (B, 1, H, W)
t_embed = t[:, None, None, None].float() / 1000
t_embed = t_embed.expand(-1, 1, x.shape[2], x.shape[3])
x_input = torch.cat([x, t_embed], dim=1)
return self.net(x_input)
# 训练过程
def train(model, diffusion, dataloader, optimizer, epochs=5):
model.train()
for epoch in range(epochs):
for x0, _ in dataloader:
x0 = x0.to(diffusion.device)
t = torch.randint(0, diffusion.T, (x0.size(0),), device=diffusion.device)
noise = torch.randn_like(x0)
xt = diffusion.q_sample(x0, t, noise)
pred_noise = model(xt, t)
loss = F.mse_loss(pred_noise, noise)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(f"Epoch {epoch} Loss: {loss.item():.4f}")
# 采样函数(反向扩散过程)
@torch.no_grad
def sample(model, diffusion, shape):
model.eval()
x = torch.randn(shape, device=diffusion.device)
for t in reversed(range(diffusion.T)):
t_tensor = torch.full((shape[0],), t, device=diffusion.device, dtype=torch.long)
z = torch.randn_like(x) if t > 0 else 0
alpha = diffusion.alphas[t]
alpha_bar = diffusion.alphas_bars[t]
beta = diffusion.betas[t]
pred_noise = model(x, t_tensor)
coef1 = 1 / torch.sqrt(alpha)
coef2 = (1 - alpha) / torch.sqrt(1 - alpha_bar)
mean = coef1 * (x - coef2 * pred_noise)
x = mean + torch.sqrt(beta) * z
return x
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
# 预处理
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Lambda(lambda x: x * 2. - 1.) # [-1, 1]
])
# 只取label为6的数据
class MNISTSixOnly(torch.utils.data.Dataset):
def __init__(self, mnist_dataset):
self.data = []
self.targets = []
for img, label in mnist_dataset:
if label == 1:
self.data.append(img)
self.targets.append(label)
self.data = torch.stack(self.data)
self.targets = torch.tensor(self.targets)
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx], self.targets[idx]
full_train_data = datasets.MNIST(root='.', train=True, transform=transform, download=True)
train_data = MNISTSixOnly(full_train_data)
print(f"[main] train_data length: {len(train_data)}")
train_loader = DataLoader(train_data, batch_size=64, shuffle=True)
# 初始化
device = 'cuda' if torch.cuda.is_available() else 'cpu'
model = SimpleDenoiseNet().to(device)
diffusion = Diffusion(T=1000, device=device)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)
MODEL_PATH = "simple_denoise_net_mnist_six.pth"
# 检查模型是否已保存,如果已保存则加载,否则训练并保存
if os.path.exists(MODEL_PATH):
print("Loading model from checkpoint...")
model.load_state_dict(torch.load(MODEL_PATH, map_location=device))
else:
print("Training model...")
train(model, diffusion, train_loader, optimizer, epochs=20)
torch.save(model.state_dict(), MODEL_PATH)
print(f"Model saved to {MODEL_PATH}")
# 采样一张图片
sample_img = sample(model, diffusion, shape=(1, 1, 28, 28))
print(f"[main] sample_img shape: {sample_img.shape}")
import matplotlib.pyplot as plt
img = sample_img[0].cpu().clamp(-1, 1) * 0.5 + 0.5 # (1, 28, 28)
img = img.squeeze(0) # (28, 28)
plt.imshow(img.numpy(), cmap='gray')
plt.axis('off')
plt.show()
print("random sample from dataset:")
import random
random_idx = random.randint(0, len(train_data) - 1)
img, label = train_data[random_idx]
# 反归一化到[0,1]区间
img_show = (img * 0.5 + 0.5).squeeze(0).numpy()
plt.figure()
plt.imshow(img_show, cmap='gray')
plt.title(f"Label: {label}")
plt.axis('off')
plt.show()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号