图像生成-PPDM-02
思想
扩散模型是一类强大的深度生成模型,它通过模仿物理学中的扩散过程来生成高质量的数据,尤其在图像生成领域取得了巨大的成功,例如大家熟知的 Stable Diffusion, Midjourney 等模型的核心技术都源于此。
理解扩散模型的核心在于理解两个相反的过程:前向过程(Forward Process)和反向过程(Reverse Process)。
核心思想:从有序到无序,再从无序中恢复有序
想象一下,你有一张清晰的猫的图片。
前向过程(加噪):我们不断地、一小步一小步地向这张图片中添加微小的“噪声”(可以理解为随机的、混乱的像素点)。经过成百上千步之后,这张清晰的图片最终会变成一张看起来完全是随机噪声的图片,原有的猫的轮廓完全消失。这个过程是固定的、无需学习的。
反向过程(去噪):现在,挑战来了。我们能否训练一个神经网络模型,让它学会这个过程的“逆操作”?也就是说,我们给模型一张纯噪声的图片,它能够一步一步地、逐渐地将噪声去除,最终还原出一张清晰的、有意义的图片(比如,一只猫)。
这个“去噪”的神经网络就是扩散模型的核心。通过在海量图片上学习这个去噪过程,模型就掌握了这些图片内在的结构和规律,从而能够“创造”出新的、从未见过的图片。
前向过程 (Forward Process)
前向过程也称为扩散过程,它是一个马尔可夫链(Markov Chain)。这意味着第 \(t\) 时刻的状态只与第 \(t-1\) 时刻的状态有关。
定义一个噪声调度表(Noise Schedule)\(β_t\) 其中 \(t\) 从 1 到 T(比如 T=1000);
\(β_t\) 是一个很小的值,它控制着每一步添加噪声的强度,并且通常随 \(t\) 增大而增大
在每一步 t,我们向上一时刻的图片 \(x_{t-1}\) 添加高斯噪声,得到 \(x_t\)。这个过程可以用下面的公式表示:
公式 1:单步加噪
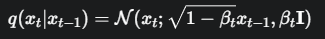
解释:
\(x_t\) 第\(t\)步得到的带噪声的图片
\(x_{t-1}\) 是上一步的图片
\(\mathcal{N}(...; \mu, \sigma^2)\)代表一个高斯分布(正态分布),\(μ\) 是均值,\(σ^2\) 是方差。
\(\sqrt{1 - \beta_t} x_{t-1}\) 是均值项。可以看到,新的图片 \(x_t\) 的主体部分仍然是 \(x_{t-1}\),只是被稍微缩放了一下
\(\beta_t \mathbf{I}\) 是方差项。\(\mathbf{I}\) 是单位协方差矩阵。这表示我们添加的噪声是一个均值为\(0\),方差为 \(β_t\) 的高斯噪声。\(β_t\) 很小,保证了每一步的噪声都很轻微。
前向过程一个非常重要的特性是,我们可以直接从原始图片 \(x_0\) 计算出任意时刻 \(t\) 的带噪图片 \(x_t\),而无需一步步迭代。这极大地简化了训练过程。
公式 2:任意步加噪(“闭式解”)

其中,\(α_t = 1 - β_t\),\(\bar{\alpha}_t = \prod_{i=1}^{t} \alpha_i\) (从 \(α_1\) 到 \(α_t\) 的累积乘积)。
这个公式告诉我们,任意时刻 \(t\) 的噪声图片 \(x_t\),可以看作是原始图片 \(x_0\) 和一个标准高斯噪声 \(ε\) 的线性组合:

其系数平方和为 1,被称为 “Nice Property”
\(\sqrt{\bar{\alpha}_t}\) 控制了原始图片信息的保留程度,\(\sqrt{1 - \bar{\alpha}_t}\) 控制了噪声的强度。当 \(t\) 越大,\(\bar{\alpha}_t\) 越小,图片越接近纯噪声。
铺垫:这个公式在训练中至关重要。因为在训练时,我们可以随机选择一个时刻 \(t\),然后用这个公式直接从原图 \(x_0\) 生成带噪样本 \(x_t\),让模型去学习如何从 \(x_t\) 预测回 \(x_0\)(或预测所加的噪声 \(ε\))。
反向过程 (Reverse Process)
反向过程是整个模型的学习核心。我们希望模型能学习 \(p(x_{t-1} | x_t)\),即从 \(t\) 时刻的噪声图片预测出 \(t-1\) 时刻的图片。理论上,如果 \(β_t\) 足够小,这个逆向过程也是一个高斯分布。
然而,我们无法直接计算这个分布,因为它需要知道所有数据的分布。因此,我们使用一个神经网络 \(p_θ\) 来近似这个真实的逆向过程 \(p\)
模型的目标:
神经网络的任务不是直接预测去噪后的图片 \(x_{t-1}\),而是去预测在 \(t\) 时刻被添加的噪声 \(ε\)。实践证明,预测噪声比直接预测图片效果更好,也更稳定。
我们将这个神经网络表示为 \(ε_θ(x_t, t)\)。它的输入是当前的噪声图片 \(x_t\) 和当前的时间步 \(t\),输出是它预测的噪声。
损失函数
模型的好坏通过损失函数来衡量。我们希望模型预测的噪声 \(ε_θ(x_t, t)\) 和当时我们实际添加的噪声 \(ε\) 尽可能的接近。最直接的方法就是使用均方误差(MSE)。
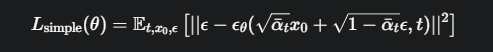
\(\mathbb{E}_{t, x_0, \epsilon}\) 表示我们在训练中会随机进行以下操作:
从训练数据集中随机抽取一张原始图片 \(x_0\)。
随机选择一个时间步 \(t\) (从 1 到 T)。
随机生成一个标准高斯噪声 \(ε\)。
\(\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon\) 就是我们前面提到的公式,用于生成带噪图片 \(x_t\)。
\(\epsilon_\theta(...)\) 是神经网络对噪声的预测
\(|| ... ||^2\) 计算了真实噪声 ε 和预测噪声 ε_θ 之间的均方误差
整个训练过程就是通过梯度下降等优化算法,不断调整神经网络的参数 \(θ\),使得这个损失函数 \(L\) 最小
核心组件:U-Net
预测噪声的神经网络 \(ε_θ\) 通常采用 U-Net 架构。
为什么是 U-Net? U-Net 最初是为医学图像分割设计的。它有一个“编码器-解码器”结构,像一个大写的'U'。
编码器(下采样):逐渐压缩图片,提取高级语义特征。
解码器(上采样):逐渐恢复图片的分辨率。
关键特性:跳跃连接 (Skip Connections)。U-Net 会将编码器中对应层级的特征图直接传递给解码器。这非常重要,因为它能帮助解码器更好地恢复图片的细节信息,防止在压缩过程中丢失。这对于像素级别的噪声预测任务来说是完美的。
代码
# model 就是我们的 U-Net
# noise_scheduler 负责管理 beta 和 alpha 的值
for step, batch in enumerate(dataloader):
# 1. 从数据加载器中获取一批原始图片 x_0
clean_images = batch['images']
# 2. 为每张图片随机采样一个时间步 t
timesteps = torch.randint(0, noise_scheduler.T, (clean_images.shape[0],))
# 3. 随机生成与图片尺寸相同的标准高斯噪声 ε
noise = torch.randn_like(clean_images)
# 4. 使用公式2计算带噪图片 x_t
noisy_images = noise_scheduler.add_noise(clean_images, noise, timesteps)
# 5. 将带噪图片和时间步送入U-Net模型,预测噪声
predicted_noise = model(noisy_images, timesteps)
# 6. 计算损失函数 (MSE)
loss = F.mse_loss(predicted_noise, noise)
# 7. 反向传播,更新模型权重
loss.backward()
optimizer.step()
optimizer.zero_grad()
生成图像(采样)流程 (伪代码)
# 从一个完全随机的噪声图像开始
image = torch.randn((1, 3, height, width)) # 假设生成一张图片
# 从最后的时间步 T 开始,循环到 1
for t in reversed(range(noise_scheduler.T)):
# 1. 将当前图像和时间步 t 送入模型预测噪声
predicted_noise = model(image, t)
# 2. 使用预测的噪声,根据一个采样公式来计算上一步的图像 x_{t-1}
# 这个公式源于对反向过程的数学推导,本质上是从 x_t 中减去预测的噪声
image = noise_scheduler.step(predicted_noise, t, image)
# 循环结束后,image 就是我们最终生成的清晰图片


 浙公网安备 33010602011771号
浙公网安备 33010602011771号