大模型- 强化学习-可信区域TRPO--88
reference
Https://newfacade.github.io/notes-on-reinforcement-learning/14-trpo.html
https://gemini.google.com/app/247cc5d3d5bad7de
论文:
https://arxiv.org/abs/1502.05477
这个相当有挑战性但非常重要的内容:可信区域策略优化 (Trust Region Policy Optimization, TRPO)。
这个算法是策略梯度(PG)方法发展史上的一个重要里程碑。要理解它,我们必须先理解它解决了什么关键问题。
背景:普通策略梯度 (PG) 方法的“致命缺陷”
之前学过的所有策略梯度方法(包括 REINFORCE 和基础 Actor-Critic)都遵循一个相似的更新规则:

(梯度上升 如何让reward期望值 最大化)
我们计算一个“好的”梯度方向 ∇J(比如用 GAE 优势加权的梯度),然后沿着这个方向走一小步,步长由学习率 α 控制。
这里的致命缺陷就在于 α 的选择:
如果 α 太小,学习过程会极其缓慢。
如果 α 太大,可能会导致“策略崩溃 (Policy Collapse)”。
一次过大的、糟糕的更新可能会让策略变得极差,导致智能体采集到非常坏的数据,进而进行更差的更新,陷入恶性循环,再也无法恢复。
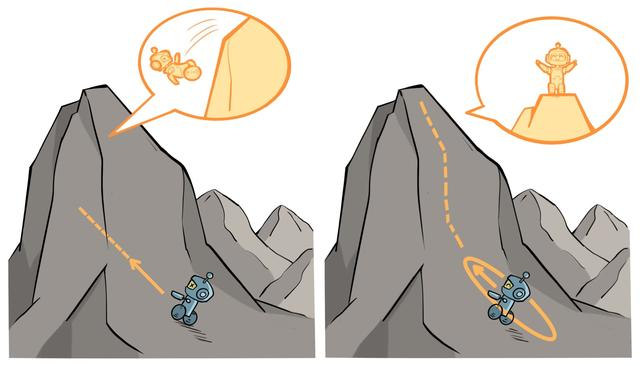
想象一下你在一个山顶上想往下走,∇J 告诉了你最陡峭的下山方向,但没告诉你该走多远。你满怀信心地迈了一大步,结果直接从悬崖上掉了下去。这就是大步长更新的风险。
TRPO 的核心思想:
能不能不要简单地设定一个固定的步长 α,而是先在当前策略周围划定一个“可信区域 (Trust Region)”,然后在这个小圈圈里,找到能让回报最大化的那个最好的新策略?只要这个圈足够小,我们就能保证新策略不会比旧的差太多,从而避免了策略崩溃。(避开坑 别往坑里踩) 在小圈圈里面找最好的policy
TRPO 的优化目标:一个带约束的数学问题(二次优化问题 可以复习一下支持向量机SVM的内容)
TRPO 将策略更新形式化成了一个严谨的、带约束的优化问题。
目标函数 (Objective Function)
想要最大化新策略 π_θ 相对于旧策略 π_{θ_old} 的期望优势。
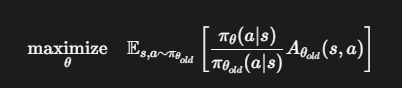
用旧策略采样数据,然后通过比率 π_θ / π_{θ_old} 来修正,从而估计新策略能带来的优势。
约束条件 (Constraint)
必须保证新策略 π_θ 和旧策略 π_{θ_old} 不要差太远。衡量两个概率分布之间“距离”的标准方法是 KL 散度 (Kullback-Leibler Divergence)

在旧策略采样的所有状态上,新旧策略的平均 KL 散度必须小于一个很小的常数 δ(例如 0.01)。δ 定义了我们的“可信区域”半径。
TRPO 的每一步更新都是在求解这个复杂的优化问题
如何求解?—— 近似与共轭梯度
1,线性近似目标函数
目标函数在 θ_old 附近进行一阶泰勒展开

g 就是在 θ_old 处的策略梯度,和我们之前见过的 ∇J 是一样的
2,二次近似约束条件
将 KL 散度约束在 θ_old 附近进行二阶泰勒展开
H 是 KL 散度在 θ_old 处的海森矩阵(Hessian Matrix),它有一个专门的名字,叫费雪信息矩阵 (Fisher Information Matrix, FIM)。
FIM 描述了参数 θ 的微小改变会对策略的概率分布产生多大影响。
海森矩阵(Hessian Matrix)可以复习一下量化的内容 GPTQ
GPTQ 描述了哪些 权重参数的量化之后对于性能影响较大
经过上面的转化后:
问题被简化成了最大化一个线性函数,同时满足一个二次约束,通过拉格朗日乘子法(二次优化问题),可以得到这个问题的解析解:

g 是普通策略梯度,告诉我们“应该往哪个方向走”。
H⁻¹ 是费雪信息矩阵的逆,它对普通梯度进行了“修正”,给那些对策略分布影响剧烈的参数方向(即 H 很大的方向)一个较小的步长,给那些影响平缓的方向一个较大的步长。
H⁻¹g 被称为自然梯度 (Natural Gradient)。它提供了一个更“聪明”、更稳健的更新方向。
实际算法:共轭梯度法 (Conjugate Gradient)
直接计算并求逆一个巨大的费雪信息矩阵 H 是不现实的,计算量极大。
TRPO 的一大创举是使用共轭梯度 (CG) 算法来求解 Hx = g 这个线性方程组,从而得到自然梯度方向 x = H⁻¹g
CG 算法的精妙之处在于,它不需要显式地计算出 H 和 H⁻¹,
只需要有能力计算费雪信息矩阵与任意向量的乘积 (Fisher-Vector Product, FVP),即 Hv 即可。这个 FVP 的计算要高效得多。
TRPO 的完整更新步骤:
- 用旧策略 π_{θ_old} 采样一批数据batch
- 使用 GAE 等方法计算优势 A(s, a) # 看上一节
- 计算普通策略梯度 g。# 看上一节
- 使用共轭梯度法,通过高效计算 FVP 来求解 Hx = g,得到自然梯度方向 x = H⁻¹g
- 计算步长,并进行线性搜索 (Line Search)。沿着自然梯度方向 x 尝试不同的步长,找到一个既能满足 KL 散度约束 δ,又能实际提升策略性能(而不是在近似模型上提升)的最好步长。
- 更新参数 θ,完成一次迭代。
代码实现(概念解读)
TRPO 的代码实现非常复杂,特别是共轭梯度和线性搜索部分。这里我们不深入具体代码,而是解读其核心组件的功能。
compute_advantage_and_gradient()
运行策略,收集数据,使用 GAE 计算优势值,并计算出普通的策略梯度 g
fisher_vector_product(v)
这是实现 CG 的关键。它接收一个向量 v,然后高效地计算并返回 H * v 的结果,全程无需构造出完整的 H 矩阵。
conjugate_gradient(g, fvp_func)
接收梯度 g 和上面定义的 FVP 函数,通过迭代求解,返回自然梯度方向 x = H⁻¹g。
update()
这是主更新函数,它会依次调用上述所有函数:计算梯度 g -> 调用 CG 得到方向 x -> 进行线性搜索找到最佳步长 -> 最后更新模型参数 θ
总结与展望
TRPO的优点:
非常稳定:通过可信区域约束,从根本上避免了策略崩溃,保证了策略性能的单调提升(或至少不会大幅下降)。
理论坚实:基于严谨的优化理论,使用了自然梯度,比简单的梯度上升更高效。
TRPO的缺点:
极其复杂:实现难度非常高,涉及到共轭梯度、线性搜索等复杂的数值优化技巧。
计算量大:虽然比直接求逆矩阵要好,但仍然属于二阶优化方法,计算开销比一阶的普通策略梯度大得多。
正是因为 TRPO 的复杂性,它的作者们后来又提出了一个“简化版”的算法,这个算法试图在不使用复杂二阶优化的情况下,达到与 TRPO 类似的稳定性和性能。这个算法就是目前最流行、最常用的策略梯度算法之一 —— PPO (Proximal Policy Optimization)
代码走读
TRPO 的代码实现确实非常复杂,但我们可以不陷入所有细枝末节,而是聚焦于其算法的核心骨架和最关键的几个计算步骤
TRPO 更新流程的整体骨架
def update():
# ------------------ 数据收集 ------------------
# 1. 用当前策略 π_old 收集一批轨迹数据 (states, actions, rewards, ...)
# 2. 计算这批数据的 GAE 优势 A(s, a) 和回报 G_t
advantages, returns = compute_advantages_and_returns()
# ------------------ TRPO 核心计算 ------------------
# 3. 计算普通策略梯度 g
policy_gradient = compute_policy_gradient(advantages)
# 4. 定义如何计算费雪-向量乘积 (FVP) 的函数,这是CG算法需要的
# 这个函数接收一个向量 v,返回 H*v
def fisher_vector_product(v):
return compute_fvp(v)
# 5. 使用共轭梯度法 (CG) 求解 Hx = g,得到搜索方向 x
search_direction = conjugate_gradient(fisher_vector_product, policy_gradient)
# 6. 进行线性搜索,找到能满足约束的最佳步长
final_step_direction = line_search(search_direction, advantages)
# ------------------ 应用更新 ------------------
# 7. 根据最终确定的方向和步长,更新策略网络参数
apply_final_update(final_step_direction)
下面,我们来详细解读其中最关键的 第 3、4、5、6 步。
计算普通策略梯度 g
这是 TRPO 的起点,和我们之前学的 Actor-Critic 类似
计算损失函数对策略网络参数 θ 的梯度 g = ∇_θ L
损失函数 L 通常是 L = - E[ log(π_θ(a|s)) * A_GAE ]
我们对这个损失函数执行一次标准的反向传播,就可以得到 g
def compute_policy_gradient(advantages):
# 从收集的数据中获取 log_probs
log_probs = get_log_probs_from_batch()
# 计算 Actor 的损失(注意负号,因为我们要最大化目标,所以最小化它的负数)
actor_loss = -(log_probs * advantages).mean()
# 使用 autograd 计算梯度,这就是 g
g = torch.autograd.grad(actor_loss, model.policy_network.parameters())
# 将梯度展平成一个一维向量
return flatten_gradients(g)
这一步是标准的策略梯度计算,主要是为了得到更新的“初始方向”。
费雪-向量乘积 (FVP) Hv
Fisher Vector Production
这是 TRPO 实现中最核心、最巧妙的部分。我们不是要构建完整的费雪信息矩阵 H,而是要创建一个能计算 H 与任意向量 v 乘积的函数。
目标:高效计算 Hv
数学原理:利用一个数学恒等式 Hv = ∇_θ ( (∇_θ D_KL) · v ),其中 · 代表点积。这个公式可以通过两次反向传播来计算,避免了构造 H。
# v 是一个与模型参数同样大小的向量
def compute_fvp(v):
# 1. 计算新旧策略的 KL 散度
# D_KL(π_old || π_new)
kl_divergence = compute_kl_divergence()
# 2. 计算 KL 散度对网络参数的梯度 (∇_θ D_KL)
# create_graph=True 是关键,它允许我们对梯度再次求导
kl_grads = torch.autograd.grad(
kl_divergence, model.policy_network.parameters(), create_graph=True
)
flat_kl_grads = flatten_gradients(kl_grads)
# 3. 计算梯度向量与输入向量 v 的点积
dot_product = torch.dot(flat_kl_grads, v)
# 4. 计算这个点积对网络参数的梯度,结果就是 H*v
fvp = torch.autograd.grad(dot_product, model.policy_network.parameters())
flat_fvp = flatten_gradients(fvp)
# 为了数值稳定性,有时会加上一个小的阻尼项
return flat_fvp + DAMPING * v
小结:这个函数是共轭梯度算法的“弹药库”,它使得在不构建H的情况下,也能利用二阶信息进行优化。
共轭梯度法 (CG)
CG 是一个经典的数值优化算法,用于求解形如 Ax=b 的线性方程组。在 TRPO 中,我们用它来求解 Hx = g。
目标:找到搜索方向 x = H⁻¹g
我们通常会直接使用一个现成的 CG 实现,或者自己写一个。它的核心是迭代。
在每次迭代中,它都会调用我们上面定义的 compute_fvp 函数来获取 H 的信息,并逐步逼近最终解 x
# 这是一个概念性的函数,实际实现会更复杂
def conjugate_gradient(fvp_func, g, max_iterations=10):
x = torch.zeros_like(g)
r = g.clone() # residual
p = g.clone() # search direction
for i in range(max_iterations):
# fvp_func 就是我们上面定义的 compute_fvp
Hp = fvp_func(p)
# ... (CG 算法的迭代更新步骤) ...
# ... 更新 x, r, p ...
return x # 返回最终的搜索方向
小结:CG 的作用就是告诉我们,结合了梯度信息 g 和曲率信息 H 之后,最优的更新方向是什么。
线性搜索 (Line Search)
CG 告诉了我们“方向”,但没告诉我们沿着这个方向“走多远”。线性搜索就是来解决这个问题的。
目标:
找到一个最佳的步长 β,使得新的参数 θ_new = θ_old + β*x 能同时满足条件:
- KL 约束:D_KL(π_old || π_new) ≤ δ
- 性能提升:新策略的真实优势 L(θ_new) 要比旧策略好
代码逻辑解读:这是一个回溯(backtracking)过程。从一个理论上的最大步长开始,不断地尝试、缩小,直到找到满足条件的步长。
def line_search(search_direction, policy_gradient, advantages):
# 1. 计算理论上的最大步长
# x^T*H*x 是对 KL 散度的二次近似,由此可算出满足约束的最大步长
xHx = torch.dot(search_direction, compute_fvp(search_direction))
max_step_length = torch.sqrt(2 * MAX_KL_DIVERGENCE / xHx)
# 2. 回溯循环:从大到小尝试步长
for i in range(BACKTRACK_ITERATIONS):
step_fraction = BACKTRACK_COEFF**i # 步长衰减因子 (如 0.8^i)
step_length = max_step_length * step_fraction
# 3. 计算尝试性的新参数
trial_step = step_length * search_direction
new_params = get_flat_params() + trial_step
# 4. 用新参数创建临时的新策略,并检查约束
# check_constraints 会同时计算新策略的真实 KL 散度和真实性能提升
actual_kl, actual_advantage_improvement = check_constraints(new_params, advantages)
# 5. 如果两个约束都满足,就返回这个最终的更新量
if actual_kl <= MAX_KL_DIVERGENCE and actual_advantage_improvement > 0:
return trial_step
# 如果循环结束都没找到,则不更新
return torch.zeros_like(search_direction)
小结:线性搜索是 TRPO 稳定性的最后一道防线,它确保了每一步更新都是“安全”且“有效”的
TRPO 的代码核心就是这一套“计算梯度 → CG找方向 → 线性搜索找步长”的精密流程。
它用复杂的二阶优化取代了简单的学习率 α,换来了无与伦比的稳定性和可靠性。虽然实现起来很有挑战,但理解了这几个核心模块的功能,你就抓住了 TRPO 算法的精髓


 浙公网安备 33010602011771号
浙公网安备 33010602011771号