大模型- 强化学习-Deep-Q-learning--82
参考
https://g.co/gemini/share/001d1d8d6fe1
https://newfacade.github.io/notes-on-reinforcement-learning/08-q-learning.html
内容
当问题变得复杂时,比如玩雅达利(Atari)游戏或者下围棋,状态空间和动作空间会变得异常巨大。如果我们还用上一讲的 Q-table 来存储每一个 Q(s, a) 的值,这张表格会大到内存完全放不下,而且智能体也几乎不可能访问到所有的状态。
为了解决这个问题,研究者们想到了用一个函数来近似(approximate)这个Q值,而不是直接存储。什么函数拟合能力最强?自然就是神经网络。
Deep Q-Network (DQN) 应运而生。它的核心思想很简单:用一个深度神经网络来代替Q-table,这个网络就叫Q网络。
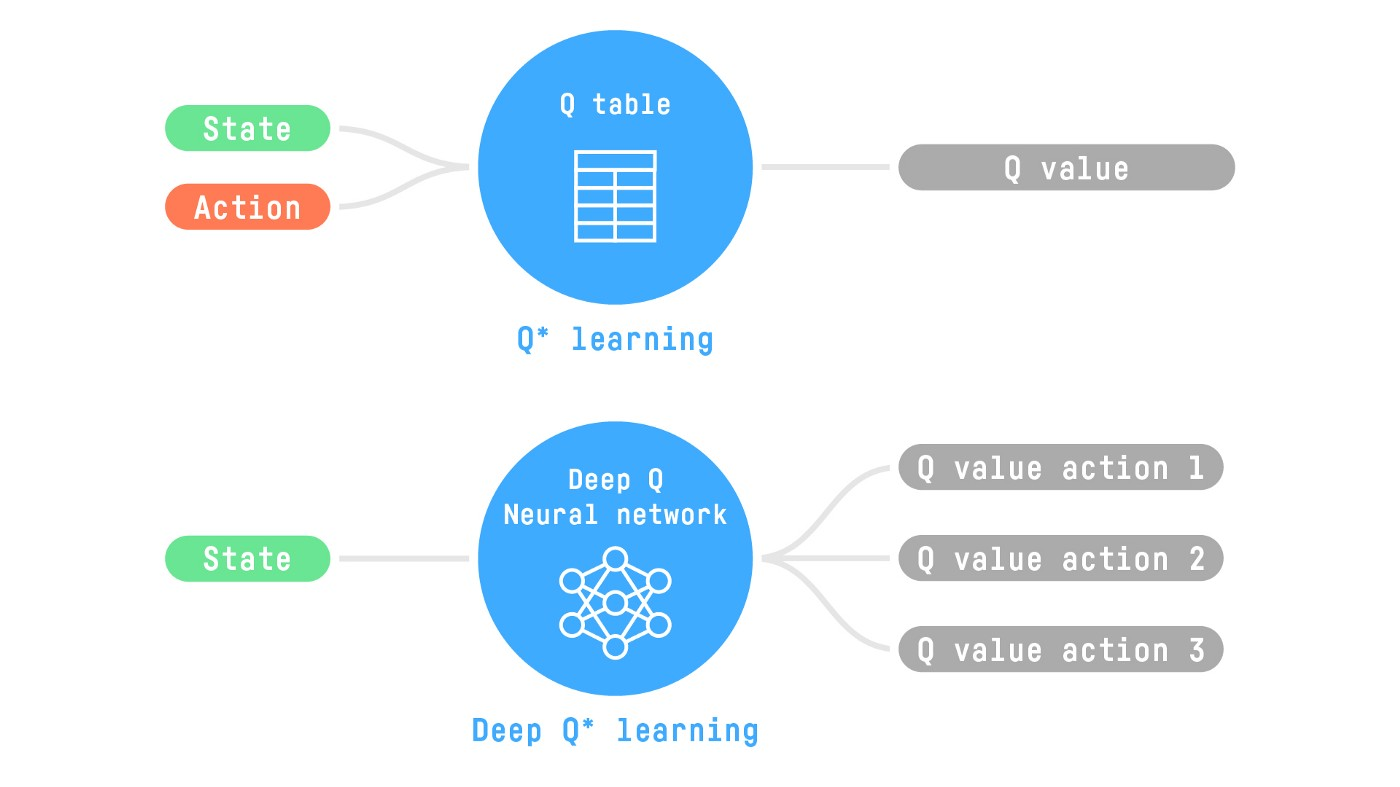
1. 从 Q-table 到 Q-Network
在传统的 Q-learning 中,我们有一个表格。而在 DQN 中,我们有一个神经网络。
输入:状态 s (比如,在雅达利游戏中,可以是游戏的原始像素图像)。
输出:一个向量,向量的每一个元素对应一个可能动作 a 的Q值。也就是说,网络一次性计算出在当前状态 s 下,所有动作的Q值。
我们用 Q(s, a; θ) 来表示这个由神经网络计算出的Q值,其中 θ 代表神经网络的所有参数(权重和偏置)。我们的目标就从“填满Q-table”变成了“找到最优的参数θ,使得 Q(s, a; θ) 能够最精确地逼近最优的动作价值函数 Q(s, a)。
如何训练 Q-Network?—— 损失函数
既然是神经网络,我们就可以用梯度下降法来训练它。训练就需要一个损失函数(Loss Function)。DQN的损失函数思想与Q-learning的TD误差一脉相承。
我们希望网络的预测值 Q(s, a; θ) 尽可能地接近 TD目标值 (TD Target)。因此,一个很自然的想法就是使用均方误差(Mean Squared Error, MSE) 作为损失函数:
这个公式看起来很美好,但实践中会遇到一个巨大的问题:不稳定。
问题出在 TD Target y = R + γ * max_{a'} Q(s', a'; θ) 上。我们用这个 y 作为监督学习中的“标签”来训练网络。但是,这个“标签”本身也是由同一个网络 Q(s, a; θ) 计算出来的。
这意味着:
我们计算出一个预测值 Q(s, a; θ)。
我们又用同一个网络计算出一个目标值 y。
然后我们根据两者的差异来更新网络参数 θ。
这就像猫在追自己的尾巴。

每当我们更新 θ 来让 Q(s, a; θ) 更接近 y 时,y 的计算方式也因为 θ 的改变而改变了。目标在不停地晃动,导致训练过程非常不稳定,很容易发散。
为了解决这个问题,DeepMind 的研究者们提出了两个关键的技巧:经验回放 (Experience Replay) 和 固定Q目标 (Fixed Q-Targets)。
技巧一:经验回放 (Experience Replay)
这个技巧的灵感来自于生物学。我们的大脑在学习新技能时,并不会只学习当下的经验,而是在休息时“回放”过去的经历来巩固学习。
工作方式:
存储: 创建一个固定大小的存储空间,称为回放缓冲区(Replay Buffer)。智能体与环境交互时,会产生大量的经验元组 e_t = (s_t, a_t, r_t, s_{t+1})。我们将这些元组都存进这个缓冲区里。
采样: 在训练神经网络时,我们不再使用刚刚产生的那个经验,而是从缓冲区中随机采样一个小批量(minibatch) 的经验 (s, a, r, s') 来进行训练
为什么有效?:
打破数据相关性: 强化学习中,智能体连续产生的经验是高度相关的(比如在游戏里,连续几帧的画面差别很小)。如果按顺序学习,会违反机器学习中数据独立同分布(i.i.d.)的假设,导致训练效率低下,模型容易陷入局部最优。随机采样打破了这种时间上的强关联,使得训练更稳定。
提高数据利用率: 每一次的经验都可能被多次采样和学习,这对于那些稀有但重要的经验(比如一次罕见的胜利或失败)尤其有价值。
技巧二:固定Q目标 (Fixed Q-Targets)
这个技巧是专门为了解决上面提到的“追尾”问题。
工作方式:
我们使用两个结构完全相同的神经网络。
一个是我们正在积极训练的主网络 (Main Network),参数为 θ。我们用它来选择动作,并计算损失函数中的“预测值”部分 Q(s, a; θ)。
另一个是目标网络 (Target Network),参数为 θ⁻。它专门用来计算TD目标值中的 max_{a'} Q(s', a'; θ⁻) 部分。
在训练开始时,我们将主网络的参数 θ 完全复制给目标网络的参数 θ⁻。
在训练过程中,我们只更新主网络的参数 θ。目标网络的参数 θ⁻ 则保持固定。
每隔 C 步训练(C 是一个超参数,比如10000步),我们再把主网络更新后的参数 θ 重新复制给目标网络 θ⁻。
通过这种方式,我们在计算TD目标时所用的网络 Q(s', a'; θ⁻) 在一段时间内是固定不变的。这就像把“追赶的目标”先钉在墙上,让主网络可以稳定地朝它前进。等追得差不多了,再把“目标”拔下来,钉到一个新的、更好的位置。
引入了固定目标网络后,我们的损失函数变为:
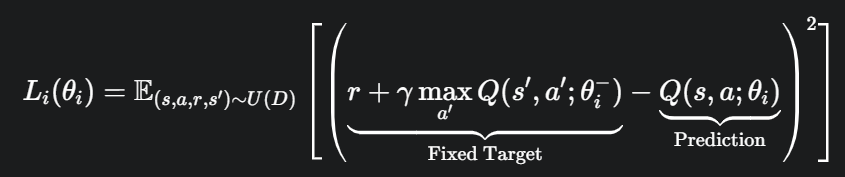
其中,θ_i 是当前主网络的参数,θ_i⁻ 是目标网络的参数,U(D) 表示从经验回放池 D 中均匀采样。
DQN 算法完整流程
结合以上所有部分,DQN的算法流程如下:
- 初始化:
初始化经验回放缓冲区 D,容量为 N。
初始化主网络 Q(s, a; θ),参数为 θ。
初始化目标网络 Q(s, a; θ⁻),参数为 θ⁻ = θ。
- 循环迭代 (for each episode):
a. 初始化状态 s。
b. 在一个 episode 内循环 (for each step t=1, T):
在状态 s,使用ε-贪心策略(基于主网络 Q(s, a; θ))选择动作 a。
执行动作 a,获得奖励 r 和新状态 s'
将经验元组 (s, a, r, s') 存入回放缓冲区 D
从 D 中随机采样一个小批量(minibatch)的经验。
对于采样的每一条经验 (s_j, a_j, r_j, s'_j),计算TD目标值:
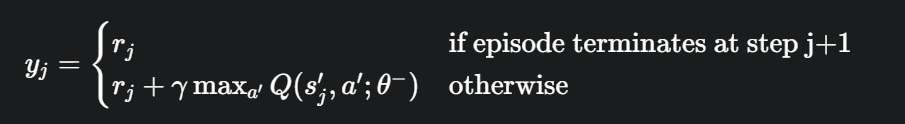
根据损失函数 L = (1/m) * Σ(y_j - Q(s_j, a_j; θ))^2,执行一步梯度下降来更新主网络参数 θ。
每 C 步,更新目标网络:θ⁻ ← θ。
更新状态:s ← s' 进入下一个状态
通过这两个关键的创新,DQN成功地将深度学习与强化学习结合起来,在许多复杂的控制任务中取得了超越人类水平的表现,是强化学习发展史上的一个重要里程碑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号