大模型- 强化学习-Q-learning--81
参考
https://newfacade.github.io/notes-on-reinforcement-learning/08-q-learning.html
https://g.co/gemini/share/0a61decbcef5
Q-learning
Q-learning 是强化学习中一个非常经典和重要的无模型（model-free）、异策略（off-policy） 的时序差分（TD）学习方法。
目标是学习一个最优的策略，这个策略能够告诉智能体（agent）在任何状态下，应该采取哪个动作才能获得最大的长期回报。
1. 核心思想：动作价值函数 Q(s, a)
强化学习的目标是最大化累积奖励。
为了实现这个目标，我们需要一个“评估标准”来判断在某个状态 s下，采取某个动作 a 到底有多好。这个评估标准就是动作价值函数（Action-Value Function），我们用 Q(s, a) 来表示。
Q(s, a) 的含义：代表在状态 s 下，执行动作 a，然后遵循某个特定策略继续往下走，所能获得的期望累积奖励。
Q-learning 的核心任务就是学习到一个最优的动作价值函数，我们称之为 Q(s, a)。
Q(s, a) 的含义：代表在状态 s 下，执行动作 a，然后遵循最优策略继续往下走，所能获得的最大期望累积奖励。
如果我们知道了这个最优的 Q(s, a)，那么在任何状态 s，我们只需要选择那个能让 Q(s, a) 值最大的动作 a，这就是最优策略了。
关键特性：异策略 (Off-policy)
这是 Q-learning 与其兄弟算法 SARSA 最主要的区别。
同策略 (On-policy)：评估和改进的策略，与智能体实际与环境交互、收集数据的策略是同一个策略。比如 SARSA，它在评估一个“ε-贪心策略”的好坏时，它自己本身也是用这个“ε-贪y心策略”去探索环境的。可以理解为“边学边用，学的就是用的”。所学即所用。
异策略 (Off-policy)：评估和改进的策略（我们称为目标策略 Target Policy），与智能体实际与环境交互、收集数据的策略（我们称为行为策略 Behavior Policy）可以不是同一个。
在 Q-learning 中：
目标策略 (Target Policy)：是一个贪心策略 (Greedy Policy)。它的目标是学习一个最优的 Q*(s, a)，所以它在更新Q值时，总是假设在下一个状态 s' 会选择那个能带来最大Q值的动作。它非常“有远见”，总是望着最好的可能性。（冷静地学习那个最优的贪心策略）
行为策略 (Behavior Policy)：通常是一个ε-贪心策略 (ε-Greedy Policy)。这个策略在大部分时候会选择当前认为最优的动作（利用），但会有 ε 的概率随机选择一个动作（探索）。这样做是为了保证算法能探索到足够多的状态-动作对，避免陷入局部最优。(大胆的去探索各种可能)
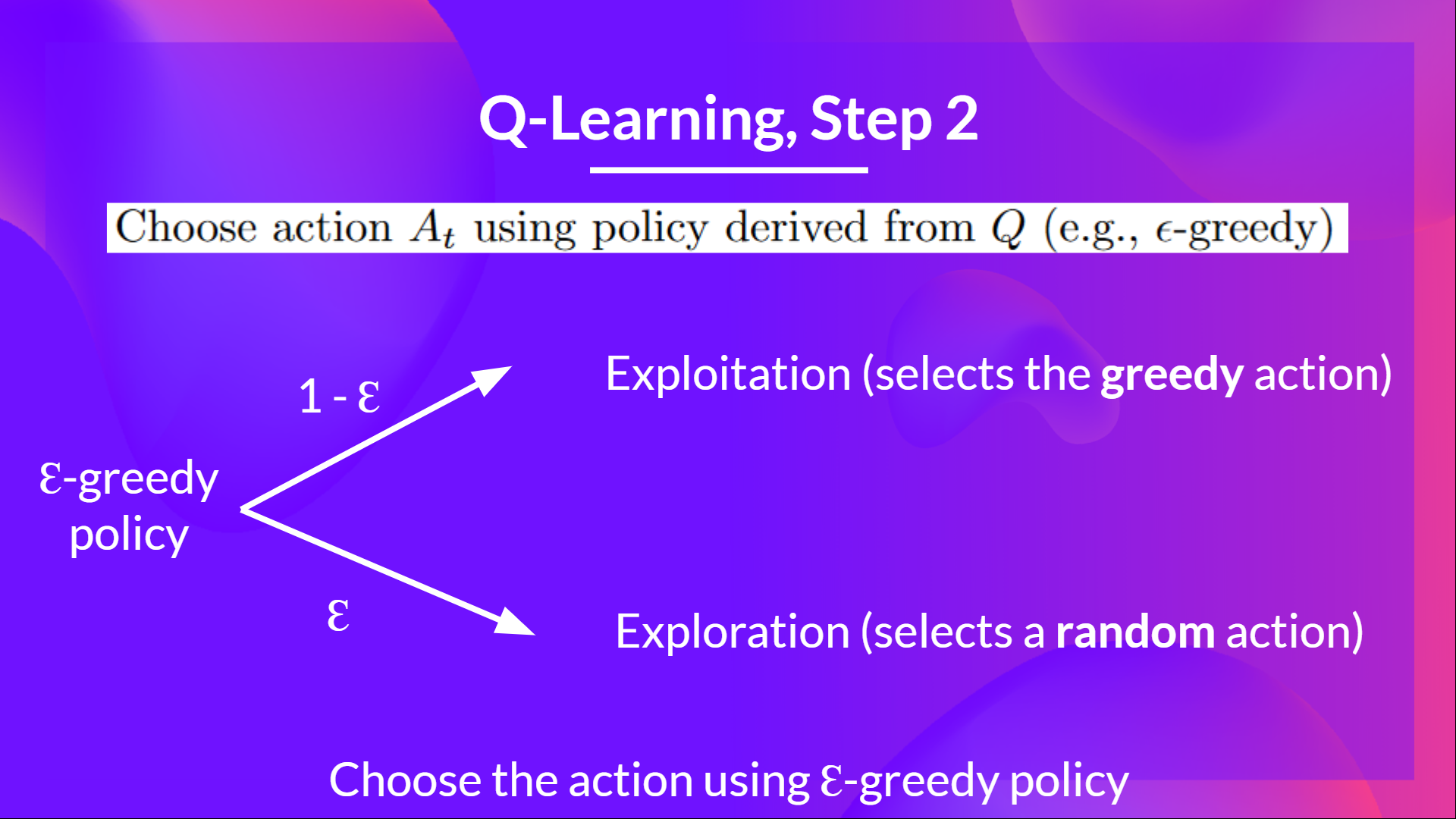
异策略的好处：它将“探索”和“学习最优策略”这两件事分开了。
行为策略负责大胆地去探索各种可能性，而目标策略则在这些探索来的经验中，冷静地学习那个最优的贪心策略。
这使得Q-learning可以利用任何策略（甚至是人类玩家）产生的数据来进行学习。
3. Q-learning 的更新公式
Q-learning 的更新公式来自于贝尔曼最优方程（Bellman Optimality Equation）的思想，并结合了时序差分（TD）的方法。
当我们处在状态 s，执行动作 a，得到奖励 R，并转移到下一个状态 s' 后，我们就得到了一个经验元组 <s, a, R, s'>。此时，我们就可以用这个经验来更新 Q(s, a) 的值。
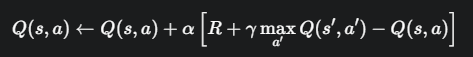
Q(s, a)：旧的Q值估计。
α (alpha)：学习率 (Learning Rate)
γ (gamma)：折扣因子 (Discount Factor)，取值在 [0, 1] 之间。它衡量了未来奖励的重要性。
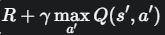这部分是TD目标值 (TD Target)，也是公式的核心。它代表了我们对 Q(s, a) 新的、更好的估计。
R 是我们立即获得的奖励。
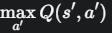体现了Q-learning的贪心本质。它在计算下一个状态的价值时，会查看在 s' 所有可能的动作 a' 中，哪个能带来最大的Q值，并把这个最大值作为下一状态的价值。这正是在模拟最优策略的行为。
这部分被称为 TD误差 (TD Error)。它代表了“新的估计值”和“旧的估计值”之间的差距。我们的学习过程，就是不断地朝着减小这个误差的方向去更新Q值。
4. Q-learning 算法流程
下面是 Q-learning 的完整算法伪代码：
初始化:
初始化一个 Q-table (一个表格，存储所有状态 s 和动作 a 对应的 Q 值)，可以全部初始化为 0，或者小的随机数。
设置学习率 α、折扣因子 γ、探索率 ε。
循环迭代 (for each episode):
a. 初始化状态 s (将智能体放到起始位置)。
b. 在一个 episode 内循环 (for each step of episode):
- 选择动作: 在当前状态 s，使用 ε-贪心策略 选择一个动作 a
- 生成一个 (0, 1) 之间的随机数，如果小于 ε，就随机选一个动作（探索）。
- 否则，就选择能使 Q(s, a) 最大的那个动作 a（利用）
- 执行动作: 执行动作 a，观察环境反馈的即时奖励 R 和下一个状态 s'。
- 更新Q表: 使用上面的Q-learning公式更新 Q(s, a) 的值。
- 更新状态: s ← s'
c. 直到 s 是一个终止状态 (episode结束)。
重复步骤，直到Q表收敛（变化很小）。
5. 与 SARSA 的对比
SARSA 是另一个非常相似的TD算法，但它是同策略 (On-policy) 的。它的名字来源于它更新时所需要的经验元组：。
SARSA 的更新公式为：
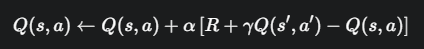
最大的区别就在于计算TD目标值的方式：
Q-learning: R + γ * max_{a'} Q(s', a')，它在 s' 状态下贪心地选择了最优动作的Q值来更新，不管实际下一步会走哪个动作。
SARSA: R + γ * Q(s', a')，它用来更新的 a'，就是行为策略（ε-贪心）在 s' 状态下实际选择的下一个动作。
一个形象的例子：
想象一个智能体在悬崖边上。
Q-learning 会学习到，虽然在悬崖边走很危险，但只要不掉下去，奖励会很高。所以它学到的Q值会比较高。它像一个勇敢的探险家，只看最优路径，不考虑路上的风险。
SARSA 因为它的行为策略（ε-贪心）有一定概率会“手滑”走出错误的一步导致掉下悬崖，所以它会把这种“探索”的风险也考虑进去。它会学到在悬崖边行走是危险的，因此会给悬崖边的状态-动作对一个较低的Q值，倾向于选择更保守安全的路径。它像一个谨慎的探险家。
代码
import math
import random
import matplotlib
import matplotlib.pyplot as plt
from collections import defaultdict
from itertools import count
import json
import gymnasium as gym
import numpy as np
env = gym.make("CartPole-v1")
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
# Q-table parameters
LEARNING_RATE = 0.2 # 增加学习率以加快学习
GAMMA = 0.99
EPSILON_START = 1.0 # 增加初始探索率
EPSILON_END = 0.01 # 降低最终探索率
EPSILON_DECAY = 2000 # 增加探索衰减时间
# Discretize continuous state space into bins
N_BINS = 20 # 增加状态空间的分辨率
state_bounds = list(zip(env.observation_space.low, env.observation_space.high))
state_bounds[1] = [-1.0, 1.0] # 扩大速度范围
state_bounds[3] = [-math.radians(60), math.radians(60)] # 扩大角度范围
def discretize_state(state):
discretized = []
for i, (s, bounds) in enumerate(zip(state, state_bounds)):
if s <= bounds[0]:
discretized.append(0)
elif s >= bounds[1]:
discretized.append(N_BINS - 1)
else:
scaling = (s - bounds[0]) / (bounds[1] - bounds[0])
new_state = int(round((N_BINS - 1) * scaling))
discretized.append(new_state)
return tuple(discretized)
# Initialize Q-table
Q = defaultdict(lambda: np.zeros(env.action_space.n))
steps_done = 0
episode_durations = []
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPSILON_END + (EPSILON_START - EPSILON_END) * \
math.exp(-1. * steps_done / EPSILON_DECAY)
steps_done += 1
if sample > eps_threshold:
return np.argmax(Q[state]) # exploitation
else:
return env.action_space.sample() # exploration
def plot_durations(show_result=False):
plt.figure(1)
durations_t = np.array(episode_durations)
if show_result:
plt.title('Result')
else:
plt.clf()
plt.title('Training...')
plt.xlabel('Episode')
plt.ylabel('Duration')
plt.plot(durations_t)
# Take 100 episode averages and plot them too
if len(durations_t) >= 100:
means = np.array([np.mean(durations_t[max(0,i-100):i]) for i in range(1, len(durations_t)+1)])
plt.plot(means)
plt.pause(0.001)
if is_ipython:
if not show_result:
display.display(plt.gcf())
display.clear_output(wait=True)
else:
display.display(plt.gcf())
def save_q_table(q_table, filename):
# Convert Q-table to regular dictionary with string keys
q_dict = {str(k): v.tolist() for k, v in q_table.items()}
with open(filename, 'w') as f:
json.dump(q_dict, f)
def load_q_table(filename):
with open(filename, 'r') as f:
q_dict = json.load(f)
# Convert back to defaultdict with tuple keys and numpy arrays
q_table = defaultdict(lambda: np.zeros(env.action_space.n))
for k, v in q_dict.items():
# Convert string tuple representation back to actual tuple
key = tuple(map(int, k.strip('()').split(',')))
q_table[key] = np.array(v)
return q_table
def train(num_episodes=5000): # 增加训练回合数
for i_episode in range(num_episodes):
state, _ = env.reset()
state = discretize_state(state)
episode_reward = 0 # 记录每个episode的总奖励
for t in count():
action = select_action(state)
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
# 修改奖励函数以加快学习
x, x_dot, theta, theta_dot = observation
# 根据状态给予更细致的奖励
reward = 1.0 # 基础奖励
reward -= abs(x) * 0.5 # 惩罚偏离中心
reward -= abs(theta) * 1.0 # 更严重地惩罚角度偏离
if done:
if t < 195: # CartPole-v1 认为195步以上为解决
reward = -20 # 增加失败惩罚
else:
reward = 20 # 增加成功奖励
if not done:
next_state = discretize_state(observation)
else:
next_state = None
# Q-learning update
if next_state is not None:
max_next_q = np.max(Q[next_state])
Q[state][action] = Q[state][action] + LEARNING_RATE * \
(reward + GAMMA * max_next_q - Q[state][action])
else:
Q[state][action] = Q[state][action] + LEARNING_RATE * \
(reward - Q[state][action])
state = next_state
episode_reward += reward
if done:
episode_durations.append(t + 1)
# 每50个episode打印一次平均持续时间和奖励
if i_episode % 50 == 0:
avg_duration = np.mean(episode_durations[-50:])
print(f'Episode {i_episode} Average Duration: {avg_duration:.2f} Episode Reward: {episode_reward:.2f}')
plot_durations()
break
print('Complete')
plot_durations(show_result=True)
plt.ioff()
plt.show()
# Save Q-table after training
save_q_table(Q, "q_table.json")
print("Q-table saved to q_table.json")
def eval_model():
global Q
# Load the trained Q-table
print("Loading Q-table from q_table.json")
Q = load_q_table("q_table.json")
env = gym.make('CartPole-v1', render_mode='rgb_array')
# 设置视频保存
from gymnasium.wrappers import RecordVideo
env = RecordVideo(env, "videos", episode_trigger=lambda x: True)
total_steps = 0
for i in range(5): # 跑5个回合看看效果
state, _ = env.reset()
state = discretize_state(state)
for t in range(500): # CartPole-v1最多500步
env.render()
action = np.argmax(Q[state]) # 选择Q值最大的动作
observation, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
if done:
total_steps += t + 1
print(f"Episode {i+1} finished after {t+1} timesteps")
break
state = discretize_state(observation)
print(f"Average steps over 5 episodes: {total_steps/5:.2f}")
env.close()
if __name__ == "__main__":
# train() # 先训练模型
eval_model() # 再评估模型
解读
这是经典的 Q-learning 算法，不是 DQN (Deep Q-Network)。它们的核心思想相似，但实现方式有本质区别。
Q-learning：使用一个表格（Q-Table）来存储每个“状态-动作”对的价值。它适用于状态空间有限且离散的环境。
DQN：使用一个深度神经网络（Deep Q-Network）来近似这个价值函数，从而处理拥有巨大或连续状态空间的环境。
这份代码通过一个巧妙的技巧——状态离散化，将 CartPole 的连续状态空间强行转换成了离散空间，从而能够使用传统的 Q-Table 来解决问题。下面我们结合理论公式，详细解读代码的每个部分，并与神经网络的实现进行比较。
核心概念：状态离散化
由于 Q-Table 无法处理连续的状态（比如角度 15.3° 和 15.4°），代码的第一步就是将连续状态“分箱”（binning），变成离散的整数。
discretize_state(state)
将环境返回的4个连续浮点数（小车位置、小车速度、杆子角度、杆子角速度）转换为一个由4个整数组成的元组，例如 (10, 8, 12, 9)
实现: 对于每个状态值，根据其在预设边界 state_bounds 内的位置，将其映射到 0 到 N_BINS - 1 的一个整数
- Q-Table (本代码): 这是使用表格的前提。但它有巨大缺陷：1) 信息丢失，15.3° 和 15.4° 可能被映射到同一个离散状态，损失了精度。2) 维度灾难，如果每个维度分20个箱，总状态数就是 202020*20 = 160,000，状态空间会随维度增加而爆炸式增长。
- DQN: 完全不需要这个步骤。神经网络可以直接处理连续的浮点数输入，它能自己学习到状态之间的细微差别，泛化能力远超离散化方法。
数据结构：Q-Table
代码使用一个 Python 的 defaultdict 来作为 Q-Table
Q = defaultdict(lambda: np.zeros(env.action_space.n))
作用: 创建一个 Q-Table。
键（key）是离散后的状态元组（如 (10, 8, 12, 9)）
值（value）是一个长度为2的NumPy数组，分别存放向左和向右两个动作的Q值，例如 [Q(s, left), Q(s, right)]。
defaultdict 的好处是，当遇到一个从未见过的状态时，会自动为它创建一个初始值为 [0., 0.] 的条目
与DQN比较:
Q-Table (本代码): 这是一个巨大的、需要显式存储的查找表。训练过程就是不断地“填”这张表。
DQN: 没有表格。取而代之的是一个神经网络 Q(s; θ)。这个网络是一个紧凑的函数，通过其内部的权重 θ 来计算任何状态 s 的Q值，而不是存储它。这极大地节省了内存，并且能够对未见过的状态进行泛化预测。
核心算法：Q-Learning 更新
训练的核心在于 train 函数中的 Q-learning 更新法则
# Q-learning update
if next_state is not None:
max_next_q = np.max(Q[next_state])
Q[state][action] = Q[state][action] + LEARNING_RATE * \
(reward + GAMMA * max_next_q - Q[state][action])
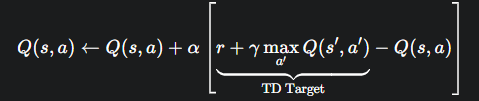
Q[state][action] 对应 Q(s,a)，即旧的Q值
LEARNING_RATE 对应学习率 alpha。
reward 对应奖励 r。
GAMMA 对应折扣因子 gamma。
max_next_q 对应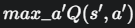
，即下一个状态能带来的最大期望回报
整个括号内的部分 (reward + GAMMA * max_next_q - Q[state][action]) 就是时序差分误差 (TD Error)
与DQN比较:
Q-Table (本代码): 更新是直接的。计算出 TD 目标后，直接修改 Q-Table 中对应 (state, action) 的那个单元格的值。
DQN: 更新是间接的，通过梯度下降完成。
计算目标 (Target): y=r+gammamax_a′Q(s′,a′;theta−)。注意，DQN 使用一个独立的、更新缓慢的目标网络 θ⁻ 来计算这个值，以增加稳定性。这是本代码没有的。
计算损失 (Loss): L(theta)=(y−Q(s,a;theta))^2计算“TD目标”和当前网络预测值之间的差距（均方误差）
梯度下降: 通过反向传播计算损失函数对网络权重 θ 的梯度，然后用优化器（如Adam）更新 θ，使得网络预测值向着TD目标靠近。
奖励塑形 (Reward Shaping)
代码对环境的原始奖励进行了修改，这是一个被称为奖励塑形的工程技巧。
reward = 1.0 # 基础奖励
reward -= abs(x) * 0.5 # 惩罚偏离中心
reward -= abs(theta) * 1.0 # 更严重地惩罚角度偏离
if done:
if t < 195:
reward = -20 # 增加失败惩罚
环境原始的奖励（每步+1）过于稀疏，智能体很难知道自己哪一步做得好、哪一步做得差。通过奖励塑形，我们给了智能体更密集、更明确的信号：
保持在中心附近是好的。
保持杆子竖直是好的。
失败是极度不好的。
奖励塑形这个技巧在 Q-learning 和 DQN 中都是通用的，它属于强化学习的工程实践，而非特定算法的一部分。一个好的奖励函数对两种方法的性能都有巨大提升。
总而言之，您的代码是学习和理解 Q-learning 核心思想的一个绝佳范例。它通过巧妙的工程技巧解决了 CartPole 问题，但其方法（状态离散化）的局限性也凸显了 DQN 等基于函数逼近的方法为何如此强大和重要。
浙公网安备 33010602011771号