poj-2782

Bin Packing

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 6410		Accepted: 2894

Description

A set of n 1-dimensional items have to be packed in identical bins. All bins have exactly the same length l and each item i has length li<=l . We look for a minimal number of bins q such that

• each bin contains at most 2 items,
• each item is packed in one of the q bins,
• the sum of the lengths of the items packed in a bin does not exceed l .

You are requested, given the integer values n , l , l1 , ..., ln , to compute the optimal number of bins q .

Input

The first line of the input contains the number of items n (1<=n<=10⁵) . The second line contains one integer that corresponds to the bin length l<=10000 . We then have n lines containing one integer value that represents the length of the items.

Output

Your program has to write the minimal number of bins required to pack all items.

Sample Input

10
80
70
15
30
35
10
80
20
35
10
30

Sample Output

6

Hint

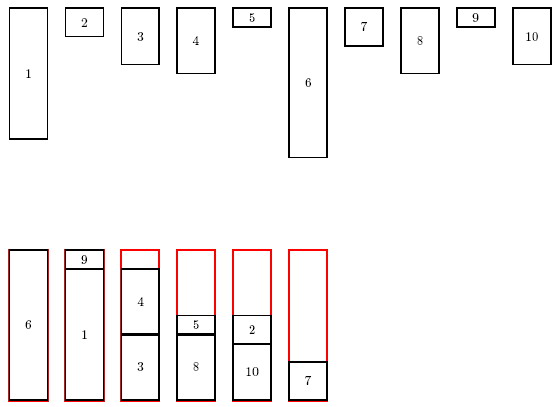
The sample instance and an optimal solution is shown in the figure below. Items are numbered from 1 to 10 according to the input order.

Source

Southwestern Europe 2005

OJ-ID：
poj-2782

author：
Caution_X

date of submission：
20191004

tags：
贪心

description modelling：
把n个东西装箱，每个东西有权值a[i]，每个箱最多装两个且最多装权值和为k，问最少要几个箱子？

major steps to solve it：
1.按权值从大到小排序
2.权值最大的东西i和权值最小的东西j装在一起同时i++,j--，如果不能把最大最小装在一起，就只装权值最大的东西同时i++

AC Code:

#include<cstdio>
#include<algorithm>
#include<time.h>
using namespace std;
int a[100005];
bool cmp(int a,int b)
{
    return a>b;
}
int main()
{
    //freopen("input.txt","r",stdin);
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0; i<n; i++) {
        scanf("%d",&a[i]);
    }
    sort(a,a+n,cmp);
    int ans=0,i=0,j=n-1;
    while(i<j) {
        if(a[i]+a[j]<=k) {
            ans++;
            i++,j--;
        }
        else {
            ans++;
            i++;
        }
    } 
    if(i==j) ans++;
    printf("%d\n",ans);
    return 0;
}