离散实验2:生成树、环路空间、断集空间的求解
实验题目:
生成树、环路空间、断集空间的求解
实验目的:
- 掌握无向连通图生成树的求解方法;
- 掌握基本回路系统和环路空间的求解方法;
- 掌握基本割集系统和断集空间的求解方法;
- 了解生成树、环路空间和断集空间的实际应用。
实验要求:
- 给定一无向简单连通图的相邻矩阵 A。
- 输出此图的关联矩阵 M。
- 求此图所有生成树个数(求方阵的行列式见参考代码) 。
- 输出其中任意一颗生成树的相邻矩阵(默认第 i 行对应顶点 vi)和关联矩阵(默认第 i 行对应顶点 vi, 第 j 列对应边 ej) 。
- 求此生成树对应的基本回路系统(输出形式如: {e1e4e3,e2e5e3})。
- 求此生成树对应的基本割集系统(输出形式如 :{{e1,e4},{e2,e5},{e3,e4,e5}})。
加分题: - 求此生成树对应的环路空间(输出形式如:{Φ,e1e4e3,e2e5e3,e1e4e5e2})。
- 求此生成树对应的断集空间(输出形式如:{Φ,{e1,e4},{e2,e5},{e3,e4,e5},{e1,e2,e4,e5},{e1,e3,e5},{e2,e3,e4},{e1,e2,e3}})。
流程图:
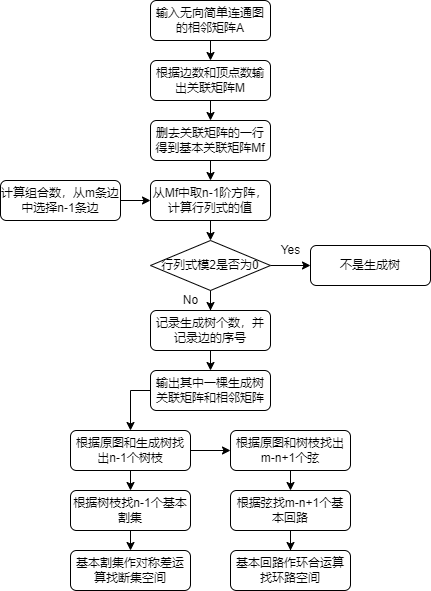
源代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<set>
#include<stack>
#include<cmath>
using namespace std;
int n = 0;//顶点数
int m = 0;//边数
int cnt;//dfs中用于计数
//使用递归算法计算行列式的值,老师给的计算行列式的函数
int valueOfMatrix(int n, vector<vector<int>> a) {
if (n == 1) {
return a[0][0];
} else if (n == 2)
return a[0][0] * a[1][1] - a[0][1] * a[1][0];
else {
int sum = 0;
for (int k = 0; k < n; k++) {
vector<vector<int>> b;
for (int i = 1; i < n; i++) {
vector<int> c;
for (int j = 0; j < n; j++) {
if (j == k)
continue;
c.push_back(a[i][j]);
}
b.push_back(c);
}
sum = k % 2 == 0 ? sum + a[0][k] * valueOfMatrix(n - 1, b) : sum - a[0][k] * valueOfMatrix(n - 1, b);
}
return sum;
}
}
//把相邻矩阵转化为关联矩阵,并把边标上序号,同时储存一条边关联的两个顶点
void convertAdjacencyToIncidence(vector<vector<int>> &A, vector<vector<int>> &M, vector<vector<int>> &edge) {
int cnt = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {//因为相邻矩阵具有对称性,所以只需要遍历下三角或者上三角
if (A[i][j] == 1) {
M[i][cnt] = 1;
M[j][cnt] = 1;
edge[cnt][0] = j;//一条边关联两个顶点
edge[cnt][1] = i;
cnt++;
}
}
}
}
//打印矩阵,因为要打印好几次矩阵,为了节约空间,所以写了一个函数用于输出矩阵
//可以打印关联矩阵或者是相邻矩阵
void printMatrix(vector<vector<int>> &M) {
printf("\n");
for (int i = 0; i < int(M.size()); i++) {
printf("v%d ", i + 1);
for (int j = 0; j < int(M[0].size()); j++) {
printf("%d ", M[i][j]);
}
printf("\n");
}
}
//求类似于组合数,从 m 条边中选 n - 1 条边,并把它们的序号数组放到一个大数组集合中,用于后续计算行列式判断生成树
void getMfs(int i, int n, int m, vector<vector<int>> &Mfs, vector<int> &Mf) {
if (n == 0) {
Mfs.push_back(Mf);
return;
} else if (n <= m - i) {
Mf.push_back(i);
getMfs(i + 1, n - 1, m, Mfs, Mf);
Mf.pop_back();
getMfs(i + 1, n, m, Mfs, Mf);
} else {
return;
}
}
//划掉关联矩阵 M 的第一行,得到基本关联矩阵 Mf,计算其中所有 n - 1 条边的组合构成的方阵的行列式,即所有 n - 1 阶方阵的行列式
//因为是数区域 F = {0, 1} ,所以计算时要将行列式取绝对值模 2 ,绝对值模 2 等于 1 为生成树,否则不是生成树
int spanTrees(vector<vector<int>> &M, vector<vector<int>> &Mfs, vector<int> &index) {
int cnt = 0;
for (int k = 0; k < int(Mfs.size()); k++) {//取 Mfs 中的第 k 个 Mf 数组
vector<vector<int>> a(n - 1, vector<int>(n - 1, 0));//数组 a 用于临时储存 n - 1 阶子方阵,方便计算行列式
for (int i = 1; i < n; i++) {//i 从 1 开始,相当于划掉关联矩阵的第一行
for (int j = 0; j < n - 1; j++) {
a[i - 1][j] = M[i][Mfs[k][j]];//Mfs 中的 Mf 中的第 k 个
}
}
if (abs(valueOfMatrix(n - 1, a))%2 == 1) {//如果行列式绝对值模 2 等于 1 则为一棵生成树
cnt++;
index.push_back(k);
}
}
return cnt;
}
//根据储存生成树边序号的数组求树枝序号的数组
void getBranches(vector<int> &Mf, vector<int> &branches) {
for (int i = 0; i < n - 1; i++) {
branches.push_back(Mf[i]);
}
cout << "树枝为:";
for (int i = 0; i < n - 1; i++) {
cout << "e" << branches[i] + 1 << " ";
}
cout << endl;
}
//根据树枝序号的数组求弦序号的数组,因为在原图中不是树枝就是弦
void getStrings(vector<int> &strings, vector<int> &branches) {
vector<int> temp(m, 0);
for (int i = 0; i < n - 1; i++) {
temp[branches[i]] = 1;
}
for (int i = 0; i < m; i++) {
if(temp[i]==0) {
strings.push_back(i);
}
}
cout << "弦为:";
for (int i = 0; i < m - n + 1; i++) {
cout << "e" << strings[i] + 1 << " ";
}
cout << endl;
}
//dfs找基本回路,基本回路由一条弦和若干个树枝构成
bool dfs(int x, int y, vector<bool> &visit, stack<int> &s, vector<vector<int>> &edge,
vector<vector<int>> &BasicCircuitSystem, vector<int> &branches) {
if (y == x) { //如果起点和终点相等,则找到一条基本回路,这个跟找欧拉回路时使用的逐步插入回路算法类似
vector<int> temp;
while (!s.empty()) { //将这条基本回路的边序号从栈中取出
int t = s.top();
temp.push_back(t);
s.pop();
}
BasicCircuitSystem.push_back(temp); //将这条基本回路放入基本回路系统中
return true;
}
//基本回路中只有一条弦,其余都是树枝
bool flag = false;
for (auto it = branches.begin(); it != branches.end(); it++) { //遍历树枝找基本回路
if (!visit[*it]) {// 若该树枝没有走过
int t = y; // t用于临时储存终点
if (edge[*it][0] == y) {
t = edge[*it][1];
} else if (edge[*it][1] == y) {
t = edge[*it][0];
} else {
continue;
}
visit[*it] = true; //走过打上标记
s.push(*it); //压入栈中
flag = true;
if (dfs(x, t, visit, s, edge, BasicCircuitSystem, branches)) { //递归
return true;
} else {//回溯
visit[*it] = false;
s.pop();
flag = false;
}
}
}
return flag;
}
//找基本回路系统,思路:和找欧拉回路时使用的逐步插入回路算法类似,使用dfs找基本回路
//因为每一条弦都对应着一条基本回路,所以需要遍历弦找出所有基本回路,所有的弦对应的基本回路构成的集合为基本回路系统
void getBasicCircuitSystem(vector<vector<int>> &BasicCircuitSystem, vector<int> &strings,
vector<int> &branches, vector<vector<int>> &edge) {
for (auto it = strings.begin(); it != strings.end(); it++) {//一条弦对应一条基本回路,遍历弦找出所有基本回路
int x = edge[*it][0];//x为弦的一个端点,即回路起点
int y = edge[*it][1];//y为弦的另一个端点,即回路终点
vector<bool> visit(m, 0);//标记边是否走过
visit[*it] = 1;
stack<int> s;//栈用于储存基本回路
s.push(*it);//把弦放入栈中
dfs(x, y, visit, s, edge, BasicCircuitSystem, branches);
}
//输出基本回路系统
cout << "基本回路系统:C基 = {";
for (int i = 0; i < m - n + 1; i++) {
for (int j = 0; j < int(BasicCircuitSystem[i].size());j++) {
cout << "e" << BasicCircuitSystem[i][j] + 1;
}
if (i != m - n) {
cout << ", ";
} else {
cout << "}" << endl;
}
}
}
//环合运算,类似于对边求对称差
void cyclization(vector<int> &a, vector<int> &b, vector<int> &temp) {
for (auto ita = a.begin(); ita != a.end(); ita++) {
bool flag = true;
for (auto itb = b.begin(); itb != b.end(); itb++) {
if (*ita == *itb) {
flag = false;
}
}
if(flag) {
temp.push_back(*ita);
}
}
for (auto itb = b.begin(); itb != b.end(); itb++) {
bool flag = true;
for (auto ita = a.begin(); ita != a.end(); ita++) {
if (*itb == *ita) {
flag = false;
}
}
if(flag) {
temp.push_back(*itb);
}
}
}
//求环路空间,求组和数,需要求 (2 ^ m-n+1) - (m-n+1) - 1 次环合
void getLoopSpace(vector<vector<int>> &BasicCircuitSystem) {
int num = m - n + 1;
if (num == 0) {//如果没有弦,直接输出空集
cout << "环路空间:C环 = {empty set}" << endl;
}
cout << "环路空间:C环 = {empty set, ";
for (int i = 0; i < m - n + 1; i++) {
for (int j = 0; j < int(BasicCircuitSystem[i].size());j++) {
cout << "e" << BasicCircuitSystem[i][j] + 1;
}
if (i != m - n) {
cout << ", ";
}
}
if (num == 1) {//如果 m-n+1 = 1 不用环合
cout << "}" << endl;
} else if (num > 1) {//如果 m-n+1 > 1 需要环合
cout << ", ";
vector<vector<int>> previous(BasicCircuitSystem);//记录上一次环合后的结果
vector<vector<int>> LoopSpace(BasicCircuitSystem);//环路空间
for (int k = 1; k < num; k++) {
vector<vector<int>> now;//记录这一次求环合的结果
for (int i = 0; i < num; i++) {
for (int j = i + 1; j < int(previous.size()); j++) {
vector<int> temp;
bool flag = true;
cyclization(BasicCircuitSystem[i], previous[j], temp);//环合运算
now.push_back(temp);
//去重,如果此次环合结果和原来结果相同,则不加入环路空间
vector<int> a(temp);
sort(a.begin(), a.end());
for (int p = 0; p < int(LoopSpace.size()); p++) {
vector<int> b(LoopSpace[p]);
sort(b.begin(), b.end());
if (a == b) {
flag = false;
break;
}
}
if(flag) {
LoopSpace.push_back(temp);
}
}
}
previous.clear();
previous.assign(now.begin(), now.end());//将此次结果记录下来
}
//打印2个及以上的环合
for (int i = num; i < int(LoopSpace.size()); i++) {
for (int j = 0; j < int(LoopSpace[i].size()); j++) {
cout << "e" << LoopSpace[i][j] + 1;
}
if (i != int(LoopSpace.size()) - 1) {
cout << ", ";
} else {
cout << "}" << endl;
}
}
}
}
//深度优先搜索
void dfs(int x, vector<vector<int>> &A, vector<bool> &visit) {
visit[x] = true;
cnt++;
for (int i = 0; i < n; i++) {
if (A[x][i] != 0 && visit[i] == 0) {
dfs(i, A, visit);
}
}
}
//dfs判断是否连通,若 cnt = n 则连通
bool isConnect(vector<vector<int>> &A, vector<bool> &visit) {
for (int i = 0; i < n; i++) {
cnt = 0;
dfs(i, A, visit);
if (cnt == n) {
return true;
}
}
return false;
}
//找基本割集系统,思路:根据生成树的相邻矩阵找基本割集,先在相邻矩阵中删除一个树枝,然后添加弦,若添加的弦能使相邻矩阵连通,
//则这条弦不在基本割集中,若添加的弦不能使相邻矩阵连通,则这条弦在基本割集中
void getBasicSegmentSystem(vector<set<int>> &BasicSegmentSystem, vector<vector<int>> &tA, vector<int> &strings,
vector<int> &branches, vector<vector<int>> &edge) {
set<int> temp;//用于存放弦的集合,方便后续求基本割集
for (auto it = strings.begin(); it != strings.end(); it++) {
temp.insert(*it);
}
for (auto it = branches.begin(); it != branches.end(); it++) {
set<int> segment(temp);//复制所有弦的集合,用于求基本割集
vector<vector<int>> ttA(tA);//复制生成树的相邻矩阵,方便后续判断是否连通
segment.insert(*it);//在基本割集中插入一个树枝,基本割集是由一个树枝和若干条弦构成的边割集
int x = edge[*it][0];
int y = edge[*it][1];
ttA[x][y] = 0;//在相邻矩阵中删除一个树枝,此时相邻矩阵不连通
ttA[y][x] = 0;
for (auto iter = strings.begin(); iter != strings.end(); iter++) {//加入一个弦判断是否连通
int x1 = edge[*iter][0];
int y1 = edge[*iter][1];
ttA[x1][y1] = 1;
ttA[y1][x1] = 1;
vector<bool> visit(n, 0);//用于判断顶点是否访问过
if(!isConnect(ttA, visit)) {//若不连通则这个弦不在基本割集中
segment.erase(*iter);
} else {//若连通则这个弦在基本割集中
ttA[x1][y1] = 0;
ttA[y1][x1] = 0;
}
}
BasicSegmentSystem.push_back(segment);
}
//输出基本割集系统
cout << "基本割集系统:S基 = {";
for (int i = 0; i < n - 1; i++) {
cout << "{";
int x = BasicSegmentSystem[i].size();
int cnt = 0;
for (auto it = BasicSegmentSystem[i].begin(); it != BasicSegmentSystem[i].end(); it++) {
cout << "e" << (*it) + 1;
cnt++;
if(cnt != x) {
cout << ",";
} else {
cout << "}";
if(i != n - 2) {
cout << ", ";
} else {
cout << "}" << endl;
}
}
}
}
}
//求对称差,两个割集求对称差
void symmetricDifference(set<int> &a, set<int> &b, set<int> &temp) {
for (auto ita = a.begin(); ita != a.end(); ita++) {
if (b.count(*ita) == 0) {
temp.insert(*ita);
}
}
for (auto itb = b.begin(); itb != b.end(); itb++) {
if (a.count(*itb) == 0) {
temp.insert(*itb);
}
}
}
//求基本割集,求组和数,需要求(2^n-1)-(n-1)-1次对称差
void getSegmentSpace(vector<set<int>>&BasicSegmentSystem) {
int num = n - 1;
if(num == 0) {//如果没有树枝直接输出空集
cout << "断集空间:S断 = {empty set}" << endl;
}
cout << "断集空间:S断 = {empty set, ";
for (int i = 0; i < n - 1; i++) {
cout << "{";
int x = BasicSegmentSystem[i].size();
int cnt = 0;
for (auto it = BasicSegmentSystem[i].begin(); it != BasicSegmentSystem[i].end(); it++) {
cout << "e" << (*it) + 1;
cnt++;
if(cnt != x) {
cout << ",";
} else {
cout << "}";
if(i != n - 2) {
cout << ", ";
}
}
}
}
if (num == 1) {//如果 n-1 = 1 不用求对称差
cout << "}" << endl;
} else if (num > 1) {//如果 n-1 > 1 需要求对称差
vector<set<int>> previous(BasicSegmentSystem);//记录上一次求对称差后的结果
vector<set<int>> SegmentSpace(BasicSegmentSystem);//断集空间
for (int k = 1; k < num; k++) {
vector<set<int>> now;//记录这一次求对称差的结果
for (int i = 0; i < num; i++) {
for (int j = i + 1; j < int(previous.size()); j++) {
set<int> temp;
bool flag = true;
//去重,如果此次求对称差结果和原来结果相同,则不加入断集空间
symmetricDifference(BasicSegmentSystem[i], previous[j], temp);
now.push_back(temp);
for (auto it = SegmentSpace.begin(); it != SegmentSpace.end(); it++) {
if (temp == *it) {
flag = false;
break;
}
}
if (temp.empty()) {
flag = false;
}
if (flag) {
SegmentSpace.push_back(temp);
}
}
}
previous.clear();
previous.assign(now.begin(), now.end());//将此次结果记录下来
}
//打印2个及以上的对称差
cout << ", ";
for (int i = num; i < int(SegmentSpace.size()); i++) {
cout << "{";
int x = SegmentSpace[i].size();
int cnt = 0;
for (auto j = SegmentSpace[i].begin(); j != SegmentSpace[i].end(); j++) {
cout << "e" << *j + 1;
cnt++;
if (cnt != x) {
cout << ",";
} else {
cout << "}";
}
}
if((i == int(SegmentSpace.size()) - 1)) {
cout << "}"<<endl;
} else {
cout << ", ";
}
}
}
}
int main() {
// m = 0;
// n = 0;
// cout << "请输入无向简单连通图的顶点数:" << endl;
// cin >> n;
// vector<vector<int>>A(n, vector<int>(n, 0));//相邻矩阵
// cout << "请输入相邻矩阵:" << endl;
// for (int i = 0; i < n; i++) {
// for (int j = 0; j < n; j++) {
// cin >> A[i][j];
// if (A[i][j] == 1) {
// m++;
// }
// }
// }
// m = m / 2;
// vector<vector<int>> A = {{0, 1, 1, 1}, {1, 0, 0, 1}, {1, 0, 0, 1}, {1, 1, 1, 0}};
// n = 4;
// m = 5;
// vector<vector<int>> A = {{0, 1, 0, 0, 1}, {1, 0, 1, 1, 1}, {0, 1, 0, 1, 0}, {0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}};
// n = 5;
// m = 7;
// vector<vector<int>> A = {{0, 1, 1, 0, 1}, {1, 0, 1, 0, 1}, {1, 1, 0, 1, 0}, {0, 0, 1, 0, 1}, {1, 1, 0, 1, 0}};
// n = 5;
// m = 7;
vector<vector<int>> A = {{0, 1, 1, 0, 0, 0}, {1, 0, 1, 0, 0, 0}, {1, 1, 0, 1, 0, 0}, {0, 0, 1, 0, 1, 1}, {0, 0, 0, 1, 0, 1}, {0, 0, 0, 1, 1, 0}};
n = 6;
m = 7;
vector<vector<int>> edge(m, vector<int>(2, 0));//储存一条边的两个顶点
cout << "相邻矩阵为:" << endl
<< " ";
for (int i = 0; i < n; i++) {
printf("v%d ", i + 1);
}
printMatrix(A);
vector<vector<int>> M(n, vector<int>(m, 0)); //关联矩阵
convertAdjacencyToIncidence(A, M, edge);
// for (int i = 0; i < m; i++) {
// cout << "边 e" << i + 1 << " 关联的两个顶点为 v" << edge[i][0] + 1 << " 和 v" << edge[i][1] + 1 << endl;
// }
cout << "关联矩阵为:" << endl
<< " ";
for (int i = 0; i < m; i++) {
printf("e%d ", i + 1);
}
printMatrix(M);
vector<vector<int>> Mfs;
vector<int> Mf;
vector<int> index;
getMfs(0, n - 1, m, Mfs, Mf);
cout << "生成树个数为:" << spanTrees(M, Mfs, index) << endl;
vector<vector<int>> tA(n, vector<int>(n, 0)); //生成树的相邻矩阵
vector<vector<int>> tM(n, vector<int>(n - 1, 0)); //生成树的关联矩阵
vector<vector<int>> tedge; //储存一条边的两个顶点
Mf = Mfs[index[0]]; //取出index中记录的第一棵生成树对应的边数组
//根据原图的关联矩阵储存生成树的关联矩阵
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
tM[i][j] = M[i][Mf[j]];
}
}
//根据生成树的关联矩阵储存生成树的相邻矩阵
for (int j = 0; j < n - 1; j++) {//根据每一条边找关联顶点
int x = 0;
int y = 0;
for (int i = 0; i < n; i++) {
if (tM[i][j] == 1) {
if (x == 0){
x = i;
} else {
y = i;
}
}
}
tA[x][y] = 1;
tA[y][x] = 1;
}
cout << "其中一棵生成树的相邻矩阵为:" << endl
<< " ";
for (int i = 0; i < n; i++) {
printf("v%d ", i + 1);
}
printMatrix(tA);
cout << "其中一棵生成树的关联矩阵为:" << endl
<< " ";
for (int i = 0; i < n - 1; i++) {
printf("e%d ", Mf[i] + 1);
}
printMatrix(tM);
vector<int> branches; // n - 1 个树枝
vector<int> strings; // m - n + 1 个弦
getBranches(Mf, branches);//找树枝
getStrings(strings, branches);//找弦
//基本回路系统,用二维数组储存,其中一个一维数组存储一个基本回路
vector<vector<int>> BasicCircuitSystem;
//基本割集系统,因为考虑到后面求基本割集系统是需要删边,所以每一个基本割集用集合储存比较方便
vector<set<int>> BasicSegmentSystem;
//找基本回路系统
getBasicCircuitSystem(BasicCircuitSystem, strings, branches, edge);
//找基本割集系统
getBasicSegmentSystem(BasicSegmentSystem, tA, strings, branches, edge);
//求环路空间
getLoopSpace(BasicCircuitSystem);
//求断集空间
getSegmentSpace(BasicSegmentSystem);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号