加法模型和向前分步算法

摘要

1. 加法模型
2. 加法模型的推导算法——向前分步算法

加法模型

在Adaboost模型中，我们把每个基本分类器合成一个复杂分类器的方法是每个基本分类器的加权和，即：

\[\begin{array}{l} f(x)=\sum_{m=1}^{M} \beta_{m} b\left(x ; \gamma_{m}\right)\\\\ b\left(x ; \gamma_{m}\right)为基本分类器\\\\ \gamma_{m}为基本分类器的参数\\\\ \beta_m为基本分类器的权重 \end{array} \]

把\(b(x ; \gamma_{m})\)看成是基函数，就可以将\(f(x)\)当做加法模型
在给定训练数据以及损失函数\(L(y, f(x))\)的条件下，学习加法模型\(f(x)\)就是：

\[\min _{\beta_{m}, \gamma_{m}} \sum_{i=1}^{N} L\left(y_{i}, \sum_{m=1}^{M} \beta_{m} b\left(x_{i} ; \gamma_{m}\right)\right) \]

通常这是一个复杂的优化问题，很难通过简单的凸优化的相关知识进行解决。
前向分步算法可以用来求解这种方式的问题，它的基本思路是：因为学习的是加法模型，如果从前向后，每一步只优化一个基函数及其系数，逐步逼近目标函数，那么就可以降低优化的复杂度。具体而言，每一步只需要优化：

\[\min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, \beta b\left(x_{i} ; \gamma\right)\right) \]

前向分步算法

给定数据集

\[\begin{array}{l} T=\{(x_1, y_1),(x_2, y_2), \cdots,(x_N, y_N)\}\\\\ x_i \in \mathcal{X} \subseteq \mathbf{R}^{n}\\\\ y_{i} \in \mathcal{Y}=\{+1,-1\} 损失函数L(y, f(x))\\\\ 基函数集合\{b(x ; \gamma)\} \end{array}\]

我们需要输出加法模型\(f(x)\)。

• 初始化：\(f_{0}(x)=0\)
• 对m = 1,2,...,M:
  • (a) 极小化损失函数：
  \[\left(\beta_{m}, \gamma_{m}\right)=\arg \min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\beta b\left(x_{i} ; \gamma\right)\right) \]
  得到参数\(\beta_{m}\)与\(\gamma_{m}\)
  • (b) 更新：
  \[f_{m}(x)=f_{m-1}(x)+\beta_{m} b\left(x ; \gamma_{m}\right) \]

• 得到加法模型：

\[f(x)=f_{M}(x)=\sum_{m=1}^{M} \beta_{m} b\left(x ; \gamma_{m}\right) \]

这样，前向分步算法将同时求解从m=1到M的所有参数\(\beta_{m}\)，\(\gamma_{m}\)的优化问题简化为逐次求解各个\(\beta_{m}\)，\(\gamma_{m}\)的问题。

GBDT(Gradient Boost Decision Tree梯度提升决策树)

基于残差学习的提升树算法（加法模型+向前分步算法）

1. GBDT是以决策树（CART）为基学习器的GB算法，是迭代树，不是分类树。

2. GBDT的核心就在于：每个基树拟合的是前一棵树的残差，真实值是预测值和残差拟合值的和。
   比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学习。

3. 伪代码：
   
   
   (1)数据处理流程

   • 输入数据集$$\begin{array}{l}
     T={(x_1, y_1),(x_2, y_2), \cdots,(x_N, y_N)}\\
     x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}\\
     y_{i} \in \mathcal{Y} \subseteq \mathbf{R}\\
     \end{array}$$
     输出最终的提升树\(f_{M}(x)\)
     
     
     (2)具体数据处理
   • 初始化\(f_0(x) = 0\)
   • 对m = 1,2,...,M：
     • 计算每个样本的残差:$$r_{m i}=y_{i}-f_{m-1}(x_{i}), \quad i=1,2, \cdots, N$$
     • 拟合残差\(r_{mi}\)学习一棵回归树，得到\(T(x ; \Theta_{m})\)
     • 更新\(f_{m}(x)=f_{m-1}(x)+T(x ; \Theta_{m})\)
     • 得到最终的回归问题的提升树：$$f_{M}(x)=\sum_{m=1}^{M} T(x ; \Theta_{m})$$

4. 实例训练：(案例来源：李航老师《统计学习方法》)
   训练数据如下表，学习这个回归问题的提升树模型，考虑只用树作为基函数。
   
   
   
   
   

至此，我们已经能够建立起依靠加法模型+前向分步算法的框架解决回归问题的算法，叫提升树算法。那么，这个算法还是否有提升的空间呢？
(2) 梯度提升决策树算法(GBDT)：
提升树利用加法模型和前向分步算法实现学习的过程，当损失函数为平方损失和指数损失时，每一步优化是相当简单的，也就是我们前面探讨的提升树算法和Adaboost算法。但是对于一般的损失函数而言，往往每一步的优化不是那么容易，针对这一问题，我们得分析问题的本质，也就是是什么导致了在一般损失函数条件下的学习困难。对比以下损失函数：

\[\begin{array}{l|l|l} \hline \text { Setting } & \text { Loss Function } & -\partial L\left(y_{i}, f\left(x_{i}\right)\right) / \partial f\left(x_{i}\right) \\ \hline \text { Regression } & \frac{1}{2}\left[y_{i}-f\left(x_{i}\right)\right]^{2} & y_{i}-f\left(x_{i}\right) \\ \hline \text { Regression } & \left|y_{i}-f\left(x_{i}\right)\right| & \operatorname{sign}\left[y_{i}-f\left(x_{i}\right)\right] \\ \hline \text { Regression } & \text { Huber } & y_{i}-f\left(x_{i}\right) \text { for }\left|y_{i}-f\left(x_{i}\right)\right| \leq \delta_{m} \\ & & \delta_{m} \operatorname{sign}\left[y_{i}-f\left(x_{i}\right)\right] \text { for }\left|y_{i}-f\left(x_{i}\right)\right|>\delta_{m} \\ & & \text { where } \delta_{m}=\alpha \text { th-quantile }\left\{\left|y_{i}-f\left(x_{i}\right)\right|\right\} \\ \hline \text { Classification } & \text { Deviance } & k \text { th component: } I\left(y_{i}=\mathcal{G}_{k}\right)-p_{k}\left(x_{i}\right) \\ \hline \end{array} \]

观察Huber损失函数：

\[L_{\delta}(y, f(x))=\left\{\begin{array}{ll} \frac{1}{2}(y-f(x))^{2} & \text { for }|y-f(x)| \leq \delta \\ \delta|y-f(x)|-\frac{1}{2} \delta^{2} & \text { otherwise } \end{array}\right. \]

针对上面的问题，Freidman提出了梯度提升算法(gradient boosting)，这是利用最速下降法的近似方法，利用损失函数的负梯度在当前模型的值\(-\left[\frac{\partial L\left(y, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}\)作为回归问题提升树算法中的残差的近似值，拟合回归树。与其说负梯度作为残差的近似值，不如说残差是负梯度的一种特例。
以下开始具体介绍梯度提升算法：
输入训练数据集\(T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}, x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}, y_{i} \in \mathcal{Y} \subseteq \mathbf{R}\)和损失函数\(L(y, f(x))\)，输出回归树\(\hat{f}(x)\)

• 初始化\(f_{0}(x)=\arg \min _{c} \sum_{i=1}^{N} L\left(y_{i}, c\right)\)
• 对于m=1,2,...,M：
  • 对i = 1,2,...,N计算：\(r_{m i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}\)
  • 对\(r_{mi}\)拟合一个回归树，得到第m棵树的叶结点区域\(R_{m j}, j=1,2, \cdots, J\)
  • 对j=1,2,...J，计算：\(c_{m j}=\arg \min _{c} \sum_{x_{i} \in R_{m j}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+c\right)\)
  • 更新\(f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)\)
• 得到回归树：\(\hat{f}(x)=f_{M}(x)=\sum_{m=1}^{M} \sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)\)

下面，我们来使用一个具体的案例来说明GBDT是如何运作的(案例来源：https://blog.csdn.net/zpalyq110/article/details/79527653 )：
下面的表格是数据：

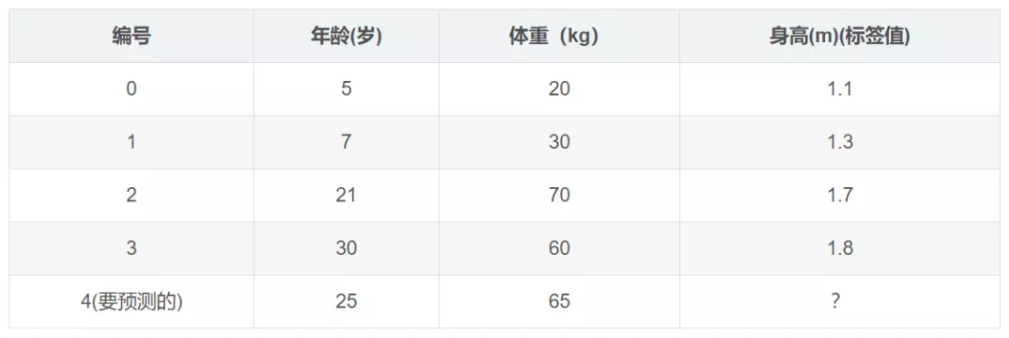
学习率：learning_rate=0.1，迭代次数：n_trees=5，树的深度：max_depth=3
平方损失的负梯度为：

\[-\left[\frac{\left.\partial L\left(y, f\left(x_{i}\right)\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{t-1}(x)}=y-f\left(x_{i}\right) \]

\(c=(1.1+1.3+1.7+1.8)/4=1.475，f_{0}(x)=c=1.475\)

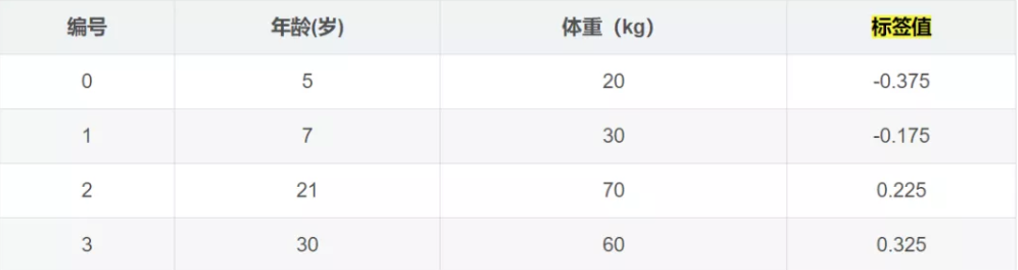
学习决策树，分裂结点：


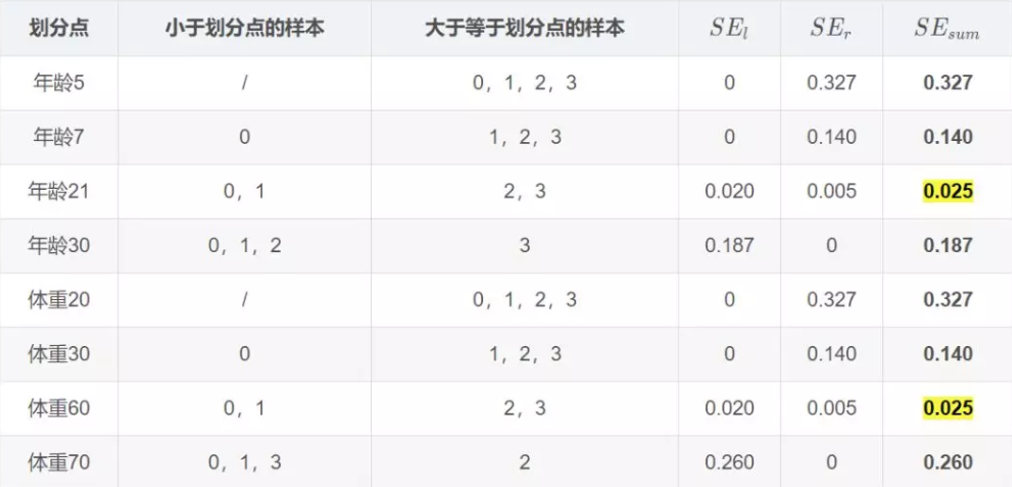
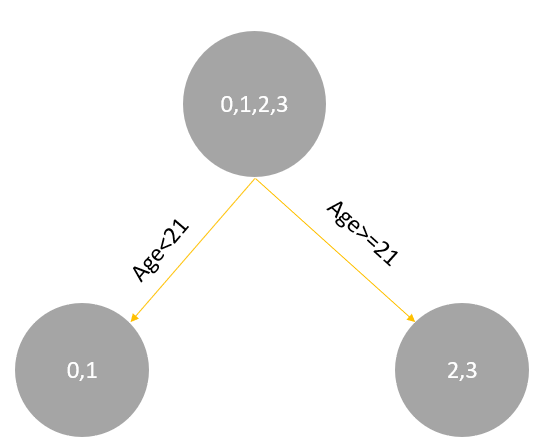
对于左节点，只有0，1两个样本，那么根据下表我们选择年龄7进行划分：

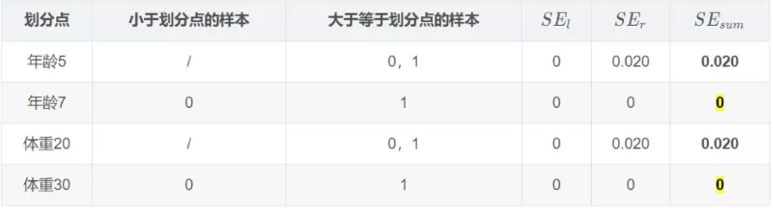
对于右节点，只有2，3两个样本，那么根据下表我们选择年龄30进行划分：

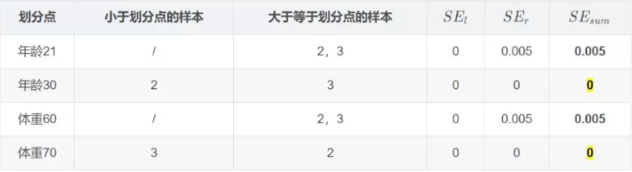
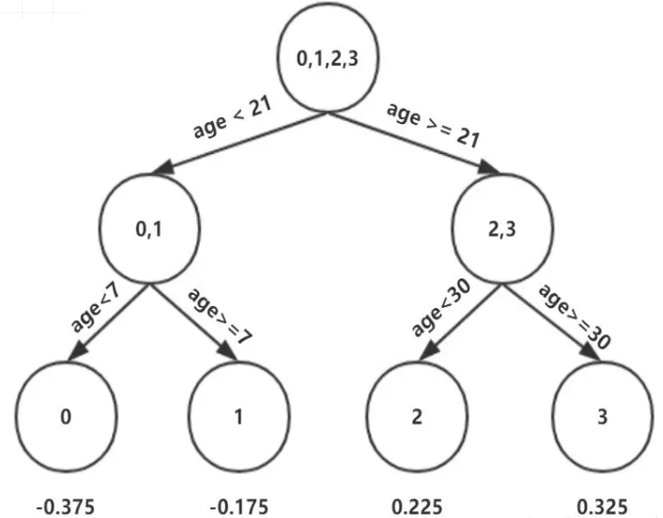
因此根据\(\Upsilon_{j 1}=\underbrace{\arg \min }_{\Upsilon} \sum_{x_{i} \in R_{j 1}} L\left(y_{i}, f_{0}\left(x_{i}\right)+\Upsilon\right)\)：

\[\begin{array}{l} \left(x_{0} \in R_{11}\right), \quad \Upsilon_{11}=-0.375 \\ \left(x_{1} \in R_{21}\right), \quad \Upsilon_{21}=-0.175 \\ \left(x_{2} \in R_{31}\right), \quad \Upsilon_{31}=0.225 \\ \left(x_{3} \in R_{41}\right), \quad \Upsilon_{41}=0.325 \end{array} \]

这里其实和上面初始化学习器是一个道理，平方损失，求导，令导数等于零，化简之后得到每个叶子节点的参数\(\Upsilon\),其实就是标签值的均值。
最后得到五轮迭代：

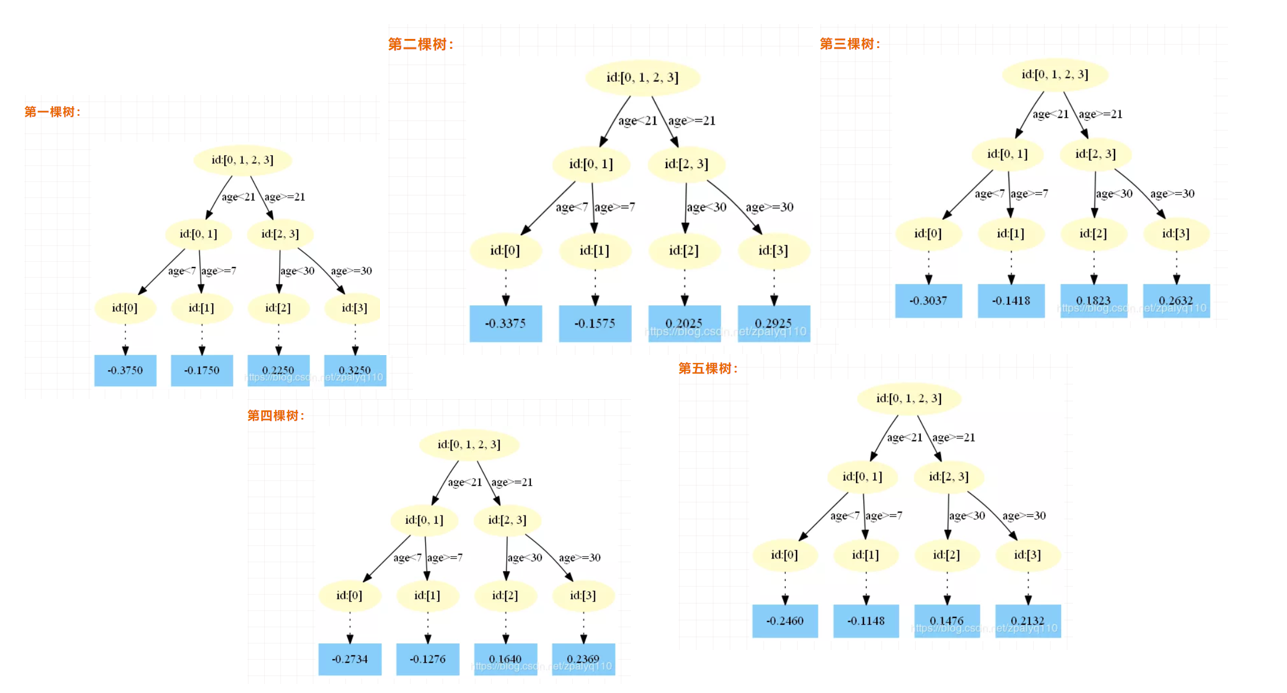
最后的强学习器为：\(f(x)=f_{5}(x)=f_{0}(x)+\sum_{m=1}^{5} \sum_{j=1}^{4} \Upsilon_{j m} I\left(x \in R_{j m}\right)\)。
其中：

\[\begin{array}{ll} f_{0}(x)=1.475 & f_{2}(x)=0.0205 \\ f_{3}(x)=0.1823 & f_{4}(x)=0.1640 \\ f_{5}(x)=0.1476 \end{array} \]

预测结果为：

\[f(x)=1.475+0.1 *(0.2250+0.2025+0.1823+0.164+0.1476)=1.56714 \]

为什么要用学习率呢？这是Shrinkage的思想，如果每次都全部加上（学习率为1）很容易一步学到位导致过拟合。

下面我们来使用sklearn来使用GBDT：
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html#sklearn.ensemble.GradientBoostingRegressor
https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingClassifier.html?highlight=gra#sklearn.ensemble.GradientBoostingClassifier

from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

'''
GradientBoostingRegressor参数解释：
loss：{‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’：‘ls’ 指最小二乘回归. ‘lad’ (最小绝对偏差) 是仅基于输入变量的顺序信息的高度鲁棒的损失函数。. ‘huber’ 是两者的结合. ‘quantile’允许分位数回归（用于alpha指定分位数）
learning_rate：学习率缩小了每棵树的贡献learning_rate。在learning_rate和n_estimators之间需要权衡。
n_estimators：要执行的提升次数。
subsample：用于拟合各个基础学习者的样本比例。如果小于1.0，则将导致随机梯度增强。subsample与参数n_estimators。选择会导致方差减少和偏差增加。subsample < 1.0
criterion：{'friedman_mse'，'mse'，'mae'}，默认='friedman_mse'：“ mse”是均方误差，“ mae”是平均绝对误差。默认值“ friedman_mse”通常是最好的，因为在某些情况下它可以提供更好的近似值。
min_samples_split：拆分内部节点所需的最少样本数
min_samples_leaf：在叶节点处需要的最小样本数。
min_weight_fraction_leaf：在所有叶节点处（所有输入样本）的权重总和中的最小加权分数。如果未提供sample_weight，则样本的权重相等。
max_depth：各个回归模型的最大深度。最大深度限制了树中节点的数量。调整此参数以获得最佳性能；最佳值取决于输入变量的相互作用。
min_impurity_decrease：如果节点分裂会导致杂质的减少大于或等于该值，则该节点将被分裂。
min_impurity_split：提前停止树木生长的阈值。如果节点的杂质高于阈值，则该节点将分裂
max_features{‘auto’, ‘sqrt’, ‘log2’}，int或float：寻找最佳分割时要考虑的功能数量：

如果为int，则max_features在每个分割处考虑特征。

如果为float，max_features则为小数，并 在每次拆分时考虑要素。int(max_features * n_features)

如果“auto”，则max_features=n_features。

如果是“ sqrt”，则max_features=sqrt(n_features)。

如果为“ log2”，则为max_features=log2(n_features)。

如果没有，则max_features=n_features。
'''

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
    max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))

from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.score(X_test, y_test)