dp背包问题

• 0-1背包

1、问题定义：

　　给定n种物品和背包。物品i的重量是w_i，价值是v_i，每种物品只有一个，背包容量为C。问：应该如何选择装入背包的物品，使得装入背包中的物品总值最大。

2、算法思路：

　　选择装入背包的物品时，对于物品i，只有两种选择，一种是装入，一种是不装入。定义m[i][j]表示背包容量为j，给定编号1-i号物品时，背包装入物品的最大价值。

初始化矩阵m：当只有物品1时，背包容量大于物品1的体积，放入。背包容量小于物品1的体积时，不放入。

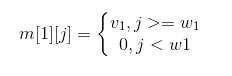
同理，对于第i件物品，如果放入可以使得背包的价值增大且不超过背包容量，就放入，反之，不放入。

 

3、具体代码：

int N = 10;
void knapsack(int *v, int *w, int c, int m[N+1][]) {
    int min = w[1] > c ? c : w[1];
    for(int j = 0; j < min; j++)
        m[1][j] = 0
    for(int j = w[1]; j <= c; j++)
        m[1][j] = v[1];
    
    for(int i = 2; i <= N; i++){
        min = w[i] > c ? c : w[i] 
        for(int j = 0; j < min; j++)
            m[i][j] = m[i-1][j];
        for(int j = w[i]; j < c; j++)
            m[i][j] = m[i-1][j-w[i]] + v[i] > m[i-1][j] ?  m[i-1][j-w[i]] + v[i] : m[i-1][j]
    }
}
//x[N+1]存放取得最大价值的背包中放入的物品，x[i] = 1表示放入了物品i，x[i] = 0表示没有放入。
void traceback(int m[N+1][], int *w, int c, int *x){
    for(int i = n; i>1; i++){
        if(m[i][c] == m[i-1][c])
            x[i] == 0;
        else
        {
            x[i] = 1;
            c -= w[i];
        }
    }
    x[1] = m[1][c] > 0 ? 1:0
}

• 完全背包

 问题定义：

　　给定n种物品和背包。物品i的重量是w_i，价值是v_i，每种物品有无限个，背包容量为C。问：应该如何选择装入背包的物品，使得装入背包中的物品总值最大。

算法思路：

　　对于0-1背包问题，是否放入第i件物品取决于选取1到i-1件物品中若干件放入背包后的状态，因为每种物品只有一件，放与不放都会影响后续物品是否能放入。对于完全背包问题，  每次加入一个新的物品类别i时，都要对背包的不同容量下的价值进行更新，因为在未加入新的物品类别i时，1-i号物品已经将背包装满了。因此m[i][j]的值与m[i-1]无关。

具体算法：

#include<iostream>
#include<string.h>
#include<limits>
using namespace std;
void C_backpack(int *v, int *w, int c, int n, int *m, int *ans){
    for(int i = 0; i <= c; i++){
        m[i] = 0;
        ans[i] = 0;
    }
    
    for(int i = 1; i <= n; i++){
        for(int j = w[i]; j <= c; j++){
            if(m[j-w[i]] + v[i] > m[j]){
                m[j] = m[j-w[i]]+v[i];
                ans[j] = i;
            }
        }
    }
}
void traceback(int *ans, int *x, int c, int *w){
    while(c > 0){
        int id = ans[c];
        x[id] ++;
        c -= w[id];
    }
}
int main(){
    int c = 11, n = 3;
//ans[i]表示当背包容积为j时放入的最后一个物品的编号，用来回溯得到每个物品被放入背包的个数
    int ans[c+1], w[n+1] = {INT_MAX, 2, 3, 1}, v[n+1] = {0, 5, 8, 2};  
    int m[c+1], x[n+1];  //记录每个物品被放入背包的个数
    memset(x , 0, sizeof(x));
    C_backpack(v, w, c, n, m, ans);
    traceback(ans, x, c, w);
    for(int i = 1; i <= n; i++)
        cout<<x[i]<<" ";
    cout<<endl;
    cout<<m[c];
}

运行结果：