递归与连接：蕨类植物分形 + 菌丝网络

世间万物，即使是最现代的事物，也依然蕴含着自然界古老的规律。

蕨类的生长并非简单的重复；它以自身为中心。每一片叶子都由更小的叶子组成，而每一片叶子又由更小的叶子组成，这种递归模式被称为自相似性。如果用数学方法将其绘制出来，你会看到一个对数螺旋或分形生长模式，其中每一片新的卷曲都以固定的比例扩展。

仿佛蕨类在每个尺度上都“记住”着自身的形状。描述它的方程，就像混沌理论中的方程一样，与定义星系和飓风的方程相同。所以，当你看到蕨类舒展开来时，你看到的是几何如何化为生命。

现在想象一下森林的秘密网络：菌丝体，真菌在地下的细丝。它们将树木、植物和土壤连接成一张庞大的活体网络。树木利用它共享养分，警告邻近的树木注意害虫，甚至跨越距离平衡化学信号。

如果把它画出来，它看起来就像一个神经网络，或者像引导数字数据在服务器间传输的路由图。这两个系统都以效率、冗余和通信为优化目标。它们之间的相似之处令人惊叹：碳基数据包和硅基数据包，都在无形的丝线上脉动。

所以，当我们观察蕨类植物或菌丝网络时，我们看到的不仅仅是生物学，我们还可以看到的是以生命形式写成的信息架构。不同之处在于，森林并非“设计”了它，而是孕育了它。

---

蕨类植物，递归的可视化。蕨类植物的螺旋不是用圆规画出来的，而是用迭代规则写成的，类似这样：

f(x, y) \rightarrow A(x, y)

其中 A 是一个变换矩阵，一个简单的几何指令。例如，著名的分形图案——巴恩斯利蕨（Barnsley fern）就是由四个这样的指令反复应用而形成的：

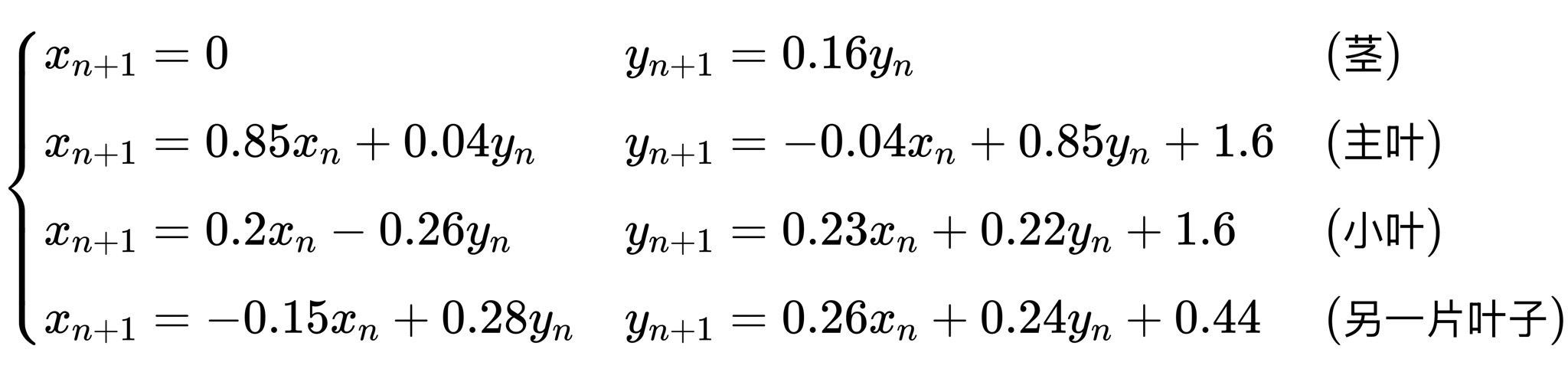
每一步都会产生一个新的点，当数十亿个这样的点累积起来，蕨类植物便逐渐成形。没有一个单独的方程可以描述蕨类植物；相反，蕨类植物源于重复，一种数学式的呼吸。

菌丝体则更像一个在空间中思考的网络。如果说蕨类植物是递归的，那么菌丝体就是分布的。它并非受单一生长规则支配，而是遵循局部优化：

 

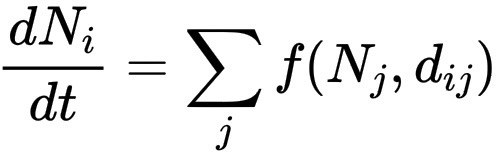
\frac{dN_i}{dt} = \sum_{j} f(N_j, d_{ij})

其中，N_i 代表营养节点，d_{ij} 代表到另一个营养节点的距离。真菌会向那些能够最大化营养流动并最小化成本的区域延伸卷须，这与计算机网络试图最小化延迟非常相似。随着时间的推移，系统会自组织成一个平衡效率和韧性的图，这与互联网架构或大脑突触中存在的二元性相同。

蕨类的生长可以被视为一个递归函数；菌丝体的生长可以被视为一个扩散函数。但两者都遵循着通过迭代涌现的更深层次原则，每个部分都遵循着简单的规则，却并未意识到它所构建的美丽。

抽象形式为：S_{t+1} = F(S_t)，其中 S 代表系统的当前状态，无论是叶尖还是菌丝节点。而 F 是转换规则。

 

---

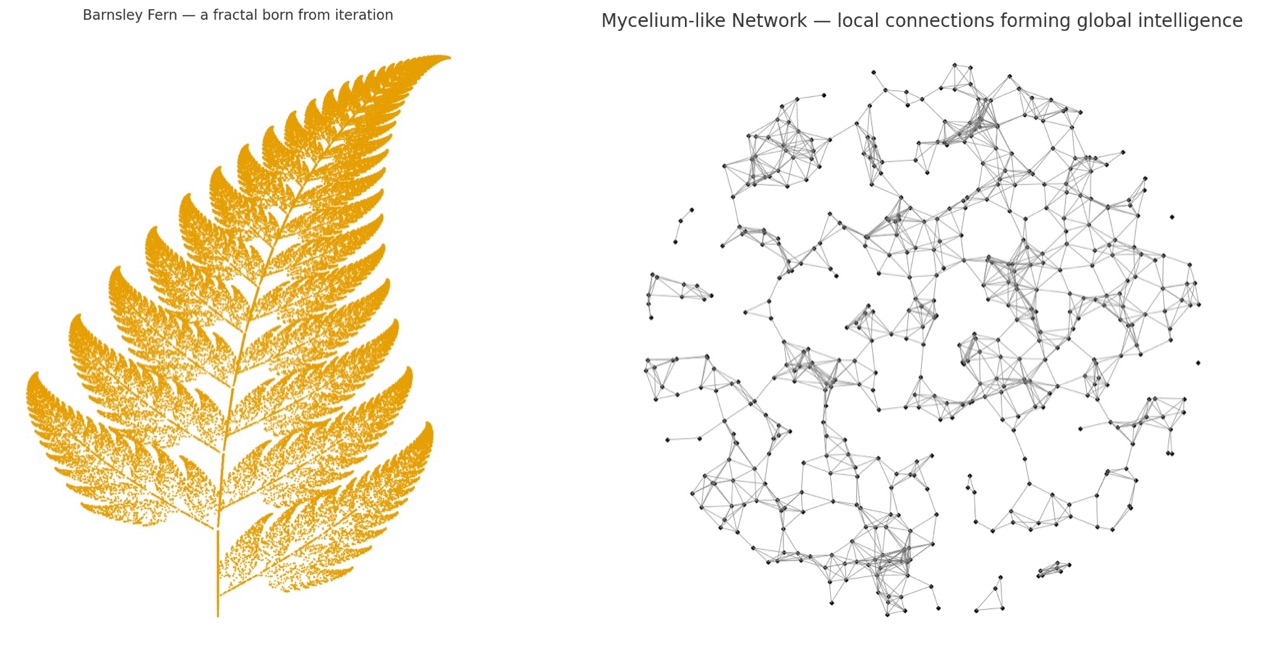
蕨类植物通过递归生长：每个部分重复一个规则，通过记忆自身的模式来构建复杂性。

菌丝体通过连接生长：每个部分对周围环境做出反应，通过相互交流来构建复杂性。

如果我们把它们结合起来，结果并非绿色分形和灰色丝线的简单混合，而是一个自相似性与网络适应性相结合的系统。换句话说：一个既能感知自身形状又能感知变化的结构。

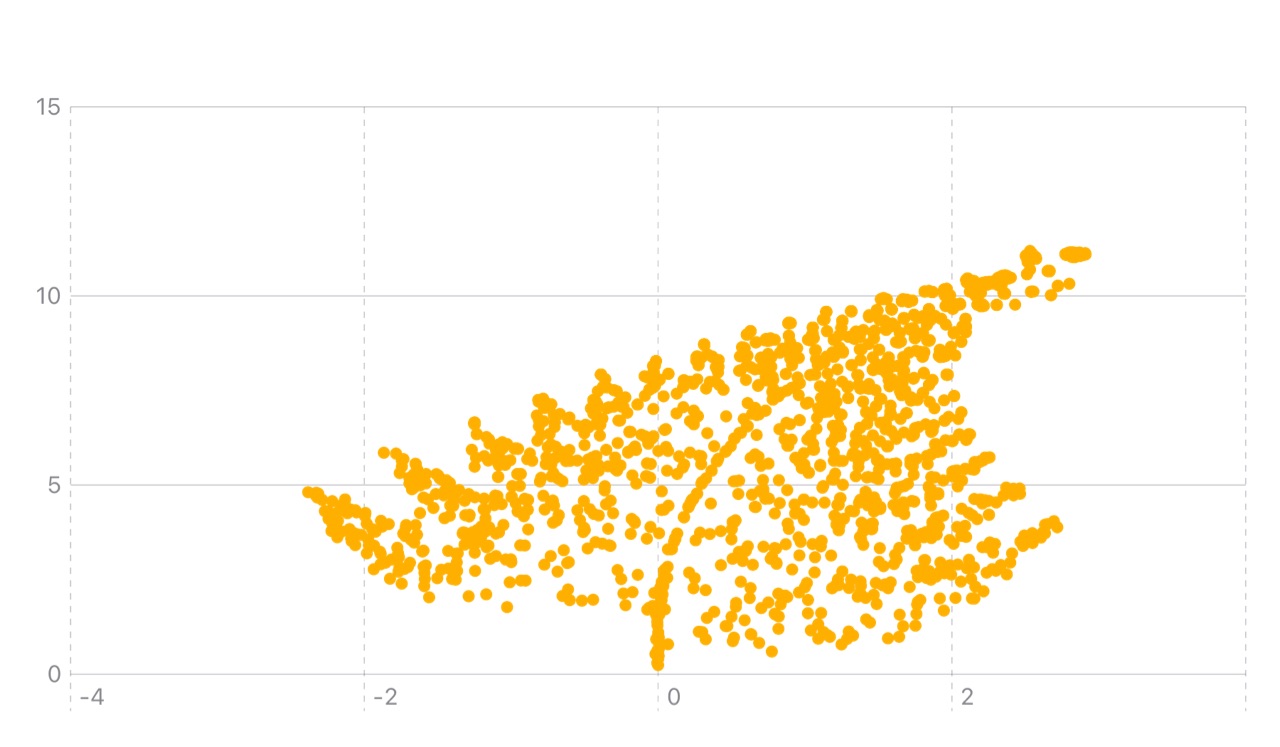
从视觉上看，这可能就像一个分形，它会根据周围的密度调整分支，就像蕨类植物在菌丝体接触的地方生长方式不同，或者像一个网络卷曲成递归螺旋状。从数学角度来说，这就像让一个递归公式（确定性）受到基于图的动态过程（随机性）的影响。我们可以在数学的世界观察当两种不同的生命逻辑开始协同作用时会发生什么。

我们可以培育出一个数学有机体，一种介于形态与交流之间的存在。

基础为自相似性（蕨类逻辑），我们从一个递归映射开始，就像蕨类植物展开的那种映射：

 

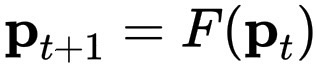
\mathbf{p}_{t+1} = F(\mathbf{p}_t)

其中 \mathbf{p}_t = (x_t, y_t) 是空间中的一个点，F 是几种仿射变换之一（拉伸、旋转、平移）。这赋予了该有机体形状记忆，它知道如何重复自身。

网络为局部感知（菌丝逻辑）。现在，让我们赋予每个点对其邻居的感知：

 

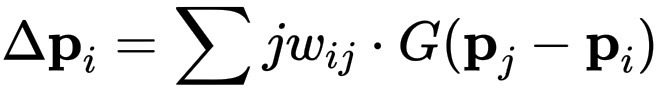
\Delta \mathbf{p}_i = \sum{j} w_{ij} \cdot G(\mathbf{p}_j - \mathbf{p}_i)

其中：w_ij 是连接权重，即两个点之间的接近程度或关联程度。G 是一个影响函数，可能是吸引力、排斥力或营养流动。这创造了适应性，生物体可以弯曲、聚集或趋向平衡。

混合体为递归与连接。为了让它们协同运作，我们将两种更新结合起来：

 

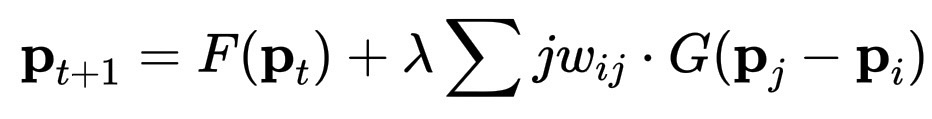
\mathbf{p}_{t+1} = F(\mathbf{p}_t) + \lambda \sum{j} w_{ij} \cdot G(\mathbf{p}_j - \mathbf{p}_i)

现在我们有了两种声音：蕨类植物项 F(\mathbf{p}_t) 赋予内部节奏，复制形态的冲动。菌丝体项增加了响应性，对环境的敏感性。这个公式描述了一个实体，它可以记住自身的模式（身份），聆听周围的世界（关系），同时平衡两者，以保持活力。

---

菌丝体函数中的 G 决定了当一个节点 i 感知到另一个节点 j 时，它会如何移动。向量 (\mathbf{p}_j - \mathbf{p}_i) 从 i 指向 j ，G 决定了这种拉力（或推力）的强度。你可以把 G 理解为生物体的敏感度曲线。不同形式的引力函数会使生物体的行为有所不同：

纯粹的吸引力 G(Δp) = Δp / ||Δp|| ，每个节点都向附近的节点漂移。结果，形成密集的聚集体，产生强大的“引力”。生物体逐渐增厚并相互交织。

带衰减的吸引力，G(Δp) = e^(-||Δp||^2 / r_0^2) Δp，附近的节点相互吸引，而远处的节点几乎不受影响。结果，形成丝状体和卷须，典型的菌丝体形态。

吸引力与排斥力的平衡，G(Δp) = (1/||Δp|| - 1/r₀) Δp/||Δp|| ，距离过近会导致彼此排斥；距离过远会导致彼此靠近。结果，有机间距，形成能够呼吸而非聚集的网络。

邻居越多越密集，所有这些 G 项的综合效应就越强：因此，在密集区域，系统会进行自组织，有时会凝聚成更粗的“根”，有时会向外扩张以寻找空间。这就是为什么在图中，你会看到蕨类的递归与菌丝的集体压力相遇时形成的分支区域，密度引导生长。