淀粉质

来看一道题

给定一棵有n个点的树
询问树上距离为k的点对是否存在。
对于30%的数据n<=100
对于60%的数据n<=1000,m<=50
对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000

首先来看一下30%的点(不要说太简单了，有时候暴力很有用)
但事实上好水啊
不是dfs的题吗？这是在你不会任何数据结构的情况下你能做的点，只需要枚举所有点对，在算出他们之间的距离，用一个标记数组将这个距离赋为1，询问的时候就直接判断距离是否为1就可以了。这样就好了，对于蒟蒻来说，会这个就可以了,但是如果你不满足这点分，继续往下看，这里就不提供代码了。

对于60%的点。
这个只要你会一点数据结构(lca)就够就可以做了，如果你不会，戳这 如果你会，这就简单了,首先预处理出每一个点到根节点的距离dis。在枚举所有点对，他们之间的距离就是dis[a]+dis[b]-2*dis[lca(a,b)];用一个标记数组将这个距离赋为1，询问的时候就直接判断距离是否为1。开氧气(O2)可以获得70分。

#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
int cnt=0,fa[500000],siz[500000],son[500000],dep[500000],top[500000],dfs[500000],head[500000],dis[500001];
struct node {
    int to,next,v;
} a[1000001];
void add(int x,int y,int c) {
    a[++cnt].to=y;
    a[cnt].next=head[x];
    a[cnt].v=c;
    head[x]=cnt;
}
void dfs1(int u,int f,int depth) {
    fa[u]=f;
    siz[u]=1;
    dep[u]=depth;
    for(int i=head[u]; i; i=a[i].next) {
        int v=a[i].to;
        if(v==f)
            continue;
        dis[v]=dis[u]+a[i].v;
        dfs1(v,u,depth+1);
        siz[u]+=siz[v];
        if(siz[v]>siz[son[u]]||son[u]==0)
            son[u]=v;
    }
}
int js;
void dfs2(int u,int t) {
    top[u]=t;
    if(son[u])
        dfs2(son[u],t);
    for(int i=head[u]; i; i=a[i].next) {
        int v=a[i].to;
        if(v!=fa[u]&&v!=son[u])
            dfs2(v,v);
    }
}
int lca(int x,int y) {
    while(top[x]!=top[y]) {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        x=fa[top[x]];
    }
    return  dep[x]<dep[y]?x:y;
}
int bj[1000001];
int main() {
    int n,m,s,x,y,v,k;
    scanf("%d%d",&n,&m);
    for(int i=1; i<n; i++)
        scanf("%d%d%d",&x,&y,&v),add(x,y,v),add(y,x,v);
    dfs1(1,0,1);
    dfs2(1,1);
    for(int i=1;i<=n;i++)
      for(int j=i+1;j<=n;j++)
            bj[dis[i]+dis[j]-2*dis[lca(i,j)]]=1;
    for(int i=1;i<=m;i++)
        scanf("%d",&k),bj[k]?printf("AYE\n"):printf("NAY\n");
}

对于100%
就要用到点分治了，现在来开始正式讲一讲点分治。

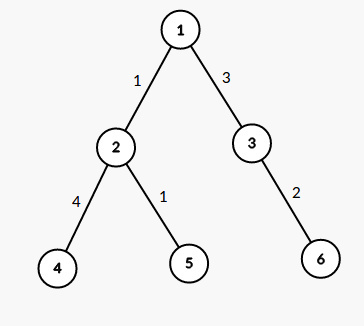
假设现在k为5。我们可以发现，对于一个根节点，有两种情况会有答案，一种是在他的子树中，另一种是从一个节点到另一个节点并且穿过他。如对于根节点1,有(1,6),(1,4)，而对于根节点2(是对于子树的根节点)，有(4,5)满足条件。

会有两种情况满足条件，那么怎么处理?分点?太麻烦了，其实可以把这两种条件看为一种条件。

1. 如果答案穿过他，分成两条路径，以上图中的(4,5)说，可以看成(2,4)+(2,5)
2. 如果答案在他的子树中，则可以看成从他的一个子节点到他本身，穿过自己，到达他自己。以(1,4)来说，可以看成(1,4)+(1,1,)。自己到自己的距离为0。

那么根节点是什么呢？不同的根节点效率会不同

1-2-3-4-5

对于这张图当以1为更节点的时候我们要递归四层,而以3为根节点话只要递归两层。所以要正确选好根节点。那么什么是最好的根节点呢？重心。

重心

什么是重心？三角形内三条中线交点？
但是这里的重心不是数学中的概念。
树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。

上面来自百度百科
实际上重心可以用一句话说明:其所有的子树中最大的子树节点数最少
那么怎么求重心呢？只要一个树形dp就可以了，接下来直接上代码，相信应该都能理解吧

在上代码之前先申明一写变量定义

int n,k;
int ans[10000001];/*储存答案*/
int dis[N];/*从当前节点i到枚举当前树的根节点父亲的距离*/(这里随便理解一下吧，我这么说是为了后面的容斥)
int f[N];/*当以i为根节点时最大子树大小*/
int vis[N];/*i节点是否被当根使用过*/
int siz[N];/*以i节点为根时,其子树(包括本身)的节点个数*/
int root;/*根节点*/
int sum;/*这棵当前递归的这棵树的大小*/

void findroot(int k,int fa) {
    f[k]=0,siz[k]=1;
    for(int i=head[k]; i; i=a[i].next) {
        int v=a[i].to;
        if(vis[v]||v==fa)
            continue;
        findroot(v,k);
        siz[k]+=siz[v];
        f[k]=max(f[k],siz[v]);
    }
    f[k]=max(f[k],sum-siz[k]);
    if(f[k]<f[root])
        root=k;
}

对于f[k]=max(f[k],sum-siz[k]);这里有很多人不知道什么意思，我下面来讲一下

继续用上面的图

假设你已经递归到了节点2，你的儿子有1,4,5(这是一个无根树)。但是你的递归并不会算1节点，所以需要这一段话来判断他的包含他"父亲"的子树大小是否时最大的。

当找到重心以后就可以找出每个点与重心的距离.在统计答案就可以了
对于这道题目可以直接n²的枚举就可以了，但对于别的题，需要别的方法，如二分。
看看这一题是如何判的

void calc(int k,int l,int c) {
    tot=0;
    finddep(k,0,l);
    for(int i=1; i<=tot; i++)
        for(int j=1; j<=tot; j++)
            ans[dis[i]+dis[j]]+=c;
}

但是对于统计答案要注意一点的就是路径会重复算。上图中如果k=7那么对于(1,4),(1,5)这也是个答案,但是这并不是个答案.路径(1,2)被算了两次.所以我们要将重复的路径去掉就可以了

那么怎么去掉呢?只要每次在递归的时候对于儿子节点,将所有儿子节点的子树满足条件的删掉就可以了,也就是dis和为k,注意这里的dis算的是所有子节点到这个儿子节点父亲的距离.

void devide(int k) {
    vis[k]=1;
    calc(k,0,1);
    for(int i=head[k]; i; i=a[i].next) {
        int v=a[i].to;
        if(vis[v])
            continue;
        calc(v,a[i].v,-1);//就是这一段话
        root=0,sum=siz[v];
        findroot(v,0);
        devide(root);
    }
}

接下来上代码

P3806 【模板】点分治1

#include<bits/stdc++.h>
#define inf 0x7fffffff
#define N 10005
using namespace std;
struct node{
    int nxt,to,v;
}edge[N<<1]; 
int n,m,ans[10000005],dis[N],vis[N],siz[N],sum,rt,mn=0x7fffffff;
int hd[N],cnt;
void add(int u,int v,int w){
    cnt++;
    edge[cnt].to=v;
    edge[cnt].nxt=hd[u];
    edge[cnt].v=w;
    hd[u]=cnt;
}
void find(int u,int fa){
    siz[u]=1,rt=0;
    int tmp=0,mn=inf;
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(vis[v] || v==fa) continue;
        find(v,u);
        siz[u]+=siz[v];
        tmp=max(tmp,siz[v]); 
    }
    tmp=max(tmp,sum-siz[u]);
    if(tmp<mn){
        mn=tmp;rt=u;
    }
}
int tot;
void finddep(int u,int fa,int l){
    dis[++tot]=l;
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(v==fa || vis[v])continue;
        finddep(v,u,l+edge[i].v);
    }
}
void calc(int u,int l,int c){
    tot=0;//
    finddep(u,0,l);
    for(int i=1;i<=tot;i++)
        for(int j=1;j<=tot;j++){
            if(i!=j)
                ans[dis[i]+dis[j]]+=c;//累加有几条
        }
}
void devide(int u){
    vis[u]=1;
    calc(u,0,1);
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(vis[v]) continue;
        calc(v,edge[i].v,-1);//减掉每一棵子树的重复的长度,一棵一棵地减 
        sum=siz[v]; 
        find(v,u);//找每一棵子树的重心 
        devide(rt) ;
    } 
}
int main(){
    int n,m,x,y,z;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n-1;i++){
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    } 
    sum=n; 
    find(1,0);
    devide(rt);
    //离线询问
    int k;
    for(int i=1;i<=m;i++){
        scanf("%d",&k);
        puts(ans[k]?"AYE":"NAY"); 
    } 
    return 0;
} 

 

P2634 [国家集训队]聪聪可可

两个点之间所有边上数的和加起来恰好是 3 的倍数，则判聪聪赢，否则可可赢。希望知道对于这张图自己的获胜概率是多少，即图中所有构成3的倍数点对数/(n*n)。

#include<bits/stdc++.h>
#define inf 0x7fffffff
#define N 200005
using namespace std;
inline int read(){
    char ch=getchar();
    int x=0,f=1;
    while((ch<'0' || ch>'9') && (ch!='-'))ch=getchar();
    if(ch=='-')f=-1,ch=getchar();
    while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*f;
}
struct node{
    int nxt,to,v;
}edge[N<<1]; 
int n,m,dis[N],vis[N],siz[N],sum,rt,book[5],dp[N];
int hd[N],cnt;
void add(int u,int v,int w){
    cnt++;
    edge[cnt].to=v;
    edge[cnt].nxt=hd[u];
    edge[cnt].v=w;
    hd[u]=cnt;
}
void find(int u,int fa){
    siz[u]=1,dp[u]=0;
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(vis[v] || v==fa) continue;
        find(v,u);
        siz[u]+=siz[v];
        dp[u]=max(dp[u],siz[v]); 
    }
    dp[u]=max(dp[u],sum-siz[u]);
    if(dp[u]<dp[rt]){
       rt=u;
    }
}
int tot;
void finddep(int u,int fa){
    book[dis[u]%3]++;
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(vis[v] || v==fa)continue;
        dis[v]=(dis[u]+edge[i].v)%3;
        finddep(v,u);
    }
}
inline int calc(int u,int l){
    memset(book,0,sizeof book);
    dis[u]=l%3;
    finddep(u,0);//这个0是父亲的意思 
    return book[0]*book[0]+book[1]*book[2]*2;
}
int ans;
void devide(int u){
    vis[u]=1;//用来求子树，中断其他子树用 
    ans+=calc(u,0);
    for(int i=hd[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(vis[v]) continue;
        ans-=calc(v,edge[i].v%3);//减掉每一棵子树的重复的长度,一棵一棵地减 
        rt=0,sum=siz[v]; //每一棵子树的大小，用来求重心用 
        find(v,u);//找每一棵子树的重心 
        devide(rt) ;
    } 
}
inline int gcd(int x,int y){
    if(x%y==0) return y;
    return gcd(y,x%y);
}
int main(){
    int n;n=read();int x,y,z;
    for(int i=1;i<=n-1;i++){
        x=read(),y=read(),z=read()%3;
        add(x,y,z);
        add(y,x,z);
    } 
    dp[0]=sum=n,rt=0; 
    find(1,0);devide(rt);
    int g=gcd(ans,n*n);
    printf("%d/%d",ans/g,(n*n)/g);
    return 0;
} 

 

点分治的时间复杂度为O(nlogn)O(nlogn)。

大致证明：

由于每次都是找数的重心，所以处理完一个大小为n的树后，它的每个子树，大小都是最大为n/2，所以最多分治logn层，每层都是n，故时间复杂度为O(nlogn)。

如果每层n个点要进行排序，那总复杂度是nlogn^2