P1325雷达
思路分析
1.显然所有雷达都应该装在海岸线上,否则被探测的面积只会少不会多。
2.无法被探测的小岛当且仅当y>dy>dy>d,这样直接输出并返回。
3.如果所有小岛都能被探测,则用结构体记录可探测第iii个小岛的雷达中xxx的最小值(lll)及最大值(rrr)(即区间)
4.将区间数组按rrr排序,这样可以按xxx从小往大遍历。
5.用变量nownownow记录目前可满足的最大x值。nownownow初始为a[1].ra[1].ra[1].r;当a[i].l>nowa[i].l>nowa[i].l>now时,说明目前的雷达不够了,需要再添雷达即ans++ans++ans++,并将nownownow的值变为a[i].ra[i].ra[i].r。
细节分析
1.区间数组的计算:勾股定理,距离disdisdis为d2−y2\sqrt{d2-y2}d2−y2
,最小值就是x−disx-disx−dis,最大值就是x+disx+disx+dis。
2.区间数组排序时,需要cmpcmpcmp函数(见代码)
代码
#include<cstdio>
#include<cmath>//用到sqrt函数
#include<algorithm>//用到sort函数
using namespace std;
const int MAXN=1010;
struct Point{//区间结构体
double l,r;
}a[MAXN];
bool cmp(Point aa,Point bb){//比较函数
return aa.r<bb.r;//按r从小到大排序
}
int main(){
int n,d,ans=1;//如题,ans=1为第一个雷达
scanf("%d%d",&n,&d);
for(int i=1;i<=n;i++){
int x,y;
scanf("%d%d",&x,&y);
if(y>d){//无法满足
printf("-1");
return 0;//直接返回
}
int dis=sqrt(d*d-y*y);//见上
a[i].l=x-dis;a[i].r=x+dis;
}
sort(a+1,a+n+1,cmp);//排序
double now=a[1].r;//见上
for(int i=2;i<=n;i++)//遍历
if(now<a[i].l){//如果不够,操作
now=a[i].r;
ans++;
}
printf("%d",ans);//输出
return 0;
}
P1031 均分纸牌改编成求最少需要多少张纸牌
可以当做往一个地方传,比如:
3 , 11, 4 都减去平均数6,则
-3, 5, -2
相当于传-3个,传2个,传0个,这个就是前缀和
a[i] = A[i] - avg, sum|sum(a[i])|, 有一个性质是一定sum[n] = 0
#include<iostream>
#include<cstdio>
using namespace std;
int a[105],cnt,sum,ans;
int main()
{
int n;cin>>n;
for(int i=1;i<=n;i++) {cin>>a[i];sum+=a[i];}
int avg=sum/n;
for(int i=1;i<=n;i++) a[i]-=avg;
for(int i=1;i<n;i++)
{
if(a[i]==0) continue;
if(a[i]!=0)
{
a[i+1]+=a[i];
ans += a[i+1];
}
}
cout<<ans<<endl;
}
哈夫曼树【k进制】
P2168 [NOI2015] 荷马史诗
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>
#define int long long
using namespace std;
struct Node{
int v, d;
bool operator < (const Node &x) const{
if(v == x.v){
return d > x.d;//优先选择高度小的
}
return v > x.v;//小根堆
}
};
priority_queue<Node> q;
int n,k,x,ans,mx,tmp;
signed main(){
scanf("%lld%lld",&n,&k);
for(int i = 1; i <= n; i++){
scanf("%lld",&x);
q.push((Node){x, 0});
}
while((q.size()-1)%(k-1)) q.push((Node){0,0});
while(q.size() != 1){
tmp = 0, mx = 0;
for(int i = 1; i <= k; i++){
tmp += q.top().v;
// cout<<"hhh: "<<q.top().v<<" "<<q.top().d<<endl;
// ans += q.top().v;
mx = max(mx, q.top().d);
q.pop();
}
// cout<<"sum:"<<sum<<" "<<mx+1<<endl;
q.push((Node){tmp, mx+1});
ans += tmp;
}
printf("%lld\n%lld\n",ans, q.top().d);
return 0;
}
/*
4 2
#
/\
1 1
*/
HAOI 糖果传递
中位数问题:有n个数,问到哪个数字的距离之和最小。\(\sum_{i=1}^{i=n}|x_i - x|\)
如果是奇数个数,则最中间的,如果是偶数个数,是n/2,还是(n+1)/2的位置呢?
其实发现,如果是偶数,n/2或者(n+1)/2都一样。
例如:
\(a_1 a_2 a_3 a_4\)
\(a_2作为中间值: (a_2 - a_1) + (a_3-a_2) +(a_4 - a_2) = - a_1 + a_4\)
\(a_3作为中间值: (a_3 - a_1) + (a_3-a_2) +(a_4 - a_3) = - a_1 + a_4\)
这道题别忽视一点:前缀和s[n] = 0。

//### 减掉平均数之后的前缀和s[n] = 0。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define int long long
using namespace std;
int agv, n, a[1000005], sum, s[1000005];
signed main(){
scanf("%lld",&n);
int v = (n+1) / 2 ;
//if(n % 2 == 0) fl = 1,v = n / 2, u = n / 2 + 1;
for(int i = 1; i <= n; i++){
scanf("%lld",&a[i]);
agv += a[i];
}
agv = agv/n;
for(int i = 1; i <= n; i++){
a[i] = a[i] - agv;
s[i] = s[i-1] + a[i];
}
sort(s+1, s+n+1);//### 所有数字选择一个减掉,使得和最小,则排序后找到中位数
for(int i = 1; i <= n; i++){
sum += abs(s[i] - s[v]);
}
printf("%lld\n", sum);
return 0;
}
P2899 [USACO08JAN]Cell Phone Network G
这道题是树上一个点可以覆盖相邻点的题,可以用贪心,也可以树形dp,但是显然树形dp要更麻烦,用来练手是一道不错的题目。 另外,一开始想到了拓扑,再一看洛谷标签有拓扑,武断写了一下拓扑的方法,首先找到叶子结点,那么叶子结点的父节点都设置信号塔,再断边,找新的叶子结点。结果惨不忍睹。 不能用拓扑的原因:
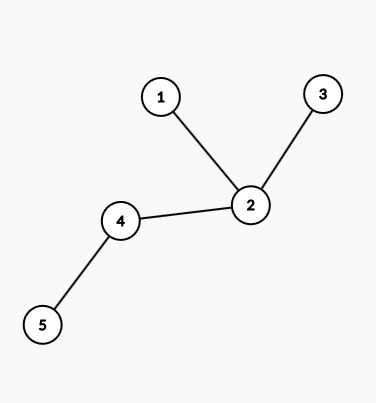
如果首先从5号点开始,则会把5、4、2全部断掉,则剩下1,3,就得设立3个信号塔,显然正解是两个。
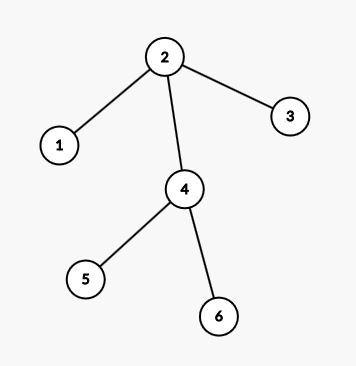
这种情况也是一样。
如果从叶子结点向内找信号塔,然后断开信号塔的地方。
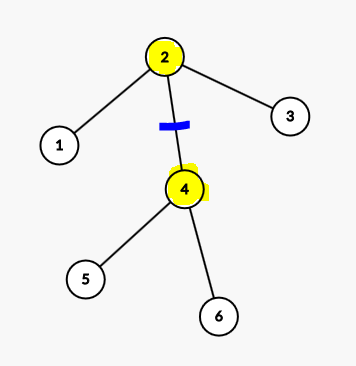
这个是可以的,但是下面的又不行了
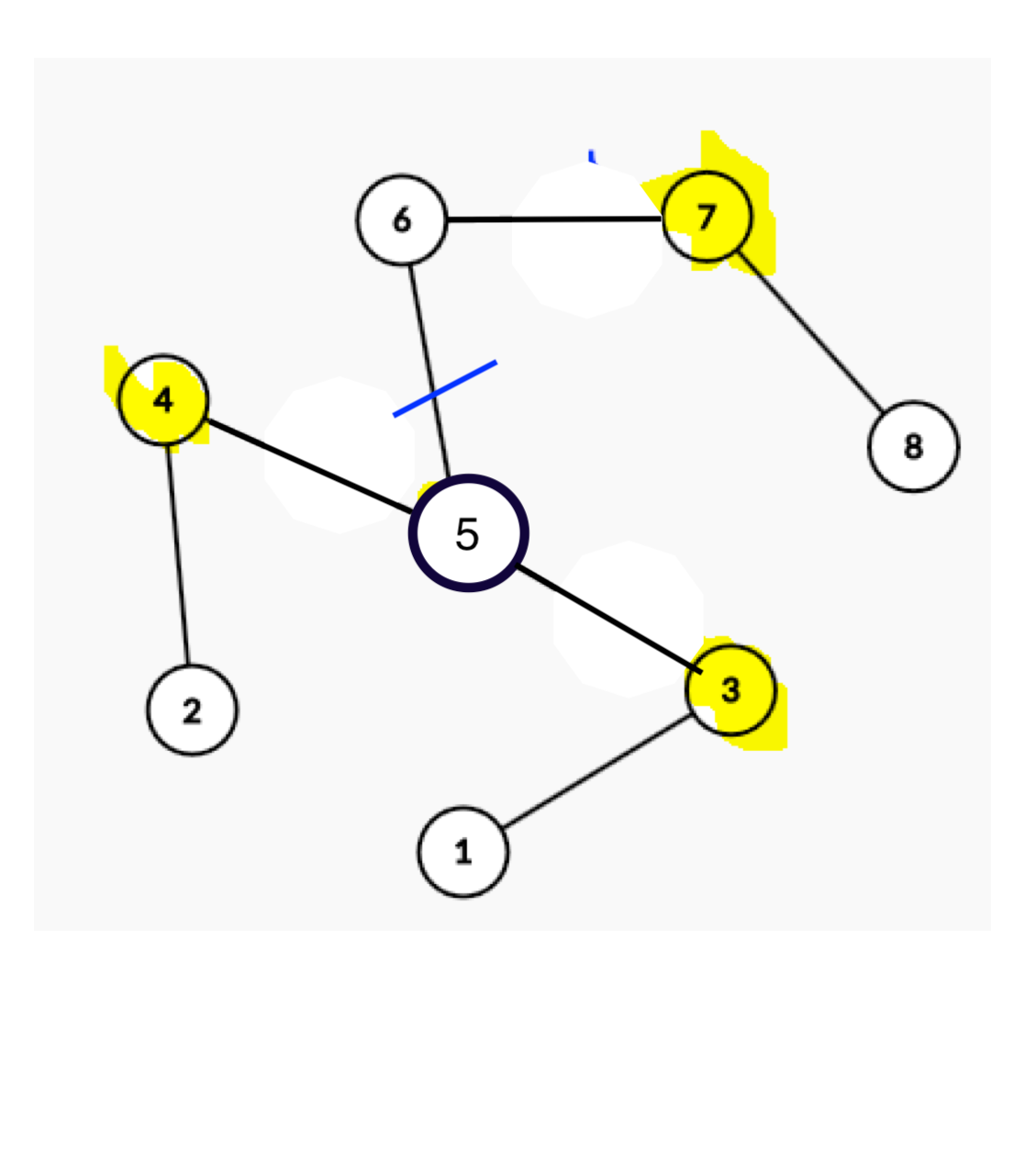
这个图应该都是中间点向三边扩充两个点,好像画错了~
因此,多次尝试以后拓扑排序是不行的。
//dp[u][0/1]表示自己设立和不设立
//dp[u][0] = min(dp[v][1] + dp[v][0/1]/dp[v][0/1])
//枚举子树中的一种必须设立 ,其余的可选可不选
//dp[u][1] = sigma(min(dp[v][0/1]) )
//-----------------------------------------------------------
//但是少考虑一种情况,u自己不设立信号塔,它是由它的父亲管辖
//这种情况是不同于u自己不设立信号塔,它是由它的子树管辖
//多写一种状态,表示自己设立,由自己管辖自己,f[u][1] = max (f[v][0/1/2])
//自己不设立,由父亲管辖自己f[u][2] = max(f[v][1/0]])
//自己不设立,由儿子管辖 f[u][0], u由哪个儿子管辖f[v][1],f[v][0],可以用一个技巧,如果所有儿子都满足这个条件f[v][0]<f[v][1],则意味着所有儿子都被孙子管着,那意味着自己没人管了,因此将所有f[v][0]都加上,且找到 f[v][1] - f[v][0] 的最小值,翻转加上。
#include<bits/stdc++.h>
using namespace std;
int n,x,y,vis[10005],dp[10005][3],cnt,hd[10005];
struct Edge{
int to,nxt;
}edge[20005];
void add(int u, int v){
cnt++;
edge[cnt].to = v;
edge[cnt].nxt = hd[u];
hd[u] = cnt;
}
void dfs(int u){
int fl = 0, mn = 0x7f7f7f7f;
dp[u][1] = 1;
for(int i = hd[u]; i; i = edge[i].nxt){
int v = edge[i].to;
if(vis[v]) continue;
vis[v] = 1;
dfs(v);
dp[u][1] += min(min(dp[v][0], dp[v][1]), dp[v][2]);
dp[u][2] += min(dp[v][1], dp[v][0]);
if(dp[v][1] <= dp[v][0]){
fl = 1;
dp[u][0] += dp[v][1];
}else{
dp[u][0] += dp[v][0];
mn = min(mn, dp[v][1] - dp[v][0]);
}
}
if(!fl){
dp[u][0] += mn;
}
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n-1; i++){
scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
// memset(dp,0x7f,sizeof dp);
vis[1] = 1; dfs(1);
printf("%d\n",min(dp[1][0], dp[1][1]));
return 0;
}
P2279消防局设立
n^2
每次找到一个最深的且没有被覆盖的点,将其爷爷标记成消防局,然后从这个点把所有距离为1和2的覆盖,再找一个最深的以此类推
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
struct Edge{
int to,next;
}e[1010];
int head[1010];
void insert(int from,int to){
static int c=0;
e[++c]=(Edge){to,head[from]};
head[from]=c;
}
int fa[1010];
bool vis[1010];
int dep[1010];
void dfs(int now,int d){
vis[now]=false;//已经被覆盖的可以再次覆盖
if (d==0) return;
for(int i=head[now]; i!=0; i=e[i].next){
dfs(e[i].to,d-1);
}
dfs(fa[now],d-1);
}
int main(){
int n;
scanf("%d",&n);
fa[1]=1;
for(int i=2; i<=n; ++i){
int a;
scanf("%d",&a);
insert(a,i);
fa[i]=a;
}
for(int i=1; i<=n; ++i)
dep[i]=dep[fa[i]]+1;
int ans=0;
memset(vis,true,sizeof(vis));//已经被覆盖的可以再次覆盖
while(1){
int t=0;
for(int i=1; i<=n; ++i){
if (vis[i]&&dep[i]>dep[t]) t=i;
}
if (t==0) break;
dfs(fa[fa[t]],2);
ans++;
}
cout<<ans;
return 0;
}
nlogn
将刚才的o(n)求最深的且没有被覆盖的改成了优先队列
#include<bits/stdc++.h>
#define maxn 1010
#define maxm 2010
using namespace std;
int head[maxn],point[maxm],nxt[maxm],dep[maxn],fa[maxn],tot=0;
bool vis[maxn];
struct Node{
int id,dep;
Node(){}
Node(int x, int y):id(x), dep(y){}
bool operator < (const Node b)const{
return dep < b.dep;
}
};
priority_queue<Node> q;
void add(int x,int y){
point[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs(int temp,int father,int depth){
fa[temp]=father;
dep[temp]=depth;
for(int j=head[temp];j;j=nxt[j]){
if(point[j]==father)
continue;
dfs(point[j],temp,depth+1);
}
}
void dfs2(int temp,int depth){
if(depth>2)
return;
vis[temp]=true;
for(int j=head[temp];j;j=nxt[j])
dfs2(point[j],depth+1);
}
int main(){
int n,cnt,x,y,ans=0;
scanf("%d",&n),cnt=n;
for(int i=1;i<=n-1;i++)
scanf("%d",&x),add(i+1,x),add(x,i+1);//建立双向边,这样就不存在向上的情况
dfs(1,0,1);
for(int i=1;i<=n;i++) q.push(Node(i,dep[i]));
while(q.size()){
while(q.size() && vis[x=q.top().id])
q.pop();
if(!q.size())
break;
if(fa[fa[x]])
dfs2(fa[fa[x]],0);
else
dfs2(1,0);
ans++;
}
printf("%d\n",ans);
return 0;
}
o(n+m)用的bfs双端队列
按照每一层存到双端队列中,从后面出队是最深的。
#include <cstdio>
#include <cstring>
#include <cctype>
#include <string>
#include <set>
#include <iostream>
#include <stack>
#include <cmath>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
int cnt, hd[1005], dep[1005], n, x, b[1005], fa[1005], tot, bbb[1005];
queue<int> q;
deque<int> p;
struct Edge{
int to, nxt;
}edge[2005];
void add(int u, int v){
cnt++;
edge[cnt].to = v;
edge[cnt].nxt = hd[u];
hd[u] = cnt;
}
void bfs(){
q.push(1), dep[1] = 1;
while(!q.empty()){
int u = q.front(); q.pop();
p.push_back(u);
for(int i = hd[u]; i; i = edge[i].nxt){
int v = edge[i].to;
if(dep[v]) continue;
q.push(v);
dep[v] = dep[u] + 1;
}
}
}
void work(int u, int fa, int d){
if(d == 0) return;
for(int i = hd[u]; i; i = edge[i].nxt){
int v = edge[i].to;
if(v == fa) continue;
b[v] = 1;
// cout<<"V: "<<v<<endl;
work(v, u, d-1);
}
}
//int vis[1005];
void dfs2(int temp,int depth){
if(depth>2) return;
b[temp]=true;
for(int j=hd[temp]; j; j=edge[j].nxt)
dfs2(edge[j].to,depth+1);
}
int main(){
scanf("%d",&n);
for(int i = 2; i <= n; i++){
scanf("%d",&x);
add(i,x);
add(x,i);
fa[i] = x;
}
bfs();
// for(int i = 1; i <= n; i++)
// cout<<i<<" "<<dep[i]<<endl;
int s = 0;
// while(!p.empty()){
// int u = p.back();
// cout<<"yyyy: "<<u<<endl; s++;
// p.pop_back();
// }
// cout<<s<<endl;
while(!p.empty()){
int u = p.back(); p.pop_back();
if(b[u]) continue;
if(fa[u] ) u = fa[u]; if(fa[u]) u = fa[u];//如果爷爷存在
if(!bbb[u]) {
// cout<<"hhh: "<<u<<endl;
b[u] = 1;
bbb[u] = 1;
tot++;
work(u, 0, 2);
}
}
printf("%d\n",tot);
return 0;
}
/*
12
1
1
3
3
5
5
6
6
6
6
10
*/
循环做法,o(n)
预处理出深度(边输入边处理)并排序,碰到已覆盖就跳过,未覆盖就在祖父处设消防站,ans++。
问题在于怎样才能判断这个点覆盖到了没有。对于儿子或孙子覆盖他,可以在在儿子处设站时就标记它;而对于父亲和祖父覆盖他,可以用儿子对父亲的映射f来解决;问题在于兄弟。其实,可以用dis数组维护“离i最近的消防站到i的距离”,当dis[父亲]==1时,就能确定它是否被覆盖。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<iostream>
#define N 2005
using namespace std;
int n, dis[N], ans, f[N];
struct Node{
int id, d;
}c[2005];
bool cmp(Node x, Node y){
return x.d > y.d;
}
int main(){
scanf("%d",&n);
c[1].id = 1; dis[0] = dis[1] = N;
for(int i = 2; i <= n; i++){
scanf("%d",&f[i]);
c[i].id = i;//它自己
c[i].d = c[f[i]].d + 1;//深度
dis[i] = N;
}
// c[1].id = 1, c[1].d = 1, c[1].f = 0;
// c[2].id = 2, c[2].d = 2, c[2].f = 1;
// c[3].id = 3, c[3].d = 3, c[3].f = 2;
// c[4].id = 4, c[4].d = 4, c[4].f = 3;
// c[5].id = 5, c[5].d = 5, c[5].f = 4;
// c[6].id = 6, c[6].d = 6, c[6].f = 5;
//sort以后
// c[1].id = 6, c[1].d = 6, c[1].f = 5
// 根据深度排序,以后深度就没用了,依次取出id
sort(c+1, c+n+1, cmp);
int t, fa, pa;
for(int i = 1; i <= n; i++){
t = c[i].id; fa = f[t]; pa = f[fa];
dis[t] = min(dis[t], min(dis[fa]+1, dis[pa]+2));
if (dis[t] > 2) {
dis[pa] = 0, ans++;
dis[f[pa]] = min(dis[f[pa]], 1);
dis[f[f[pa]]] = min(dis[f[f[pa]]], 2);
}
}
printf("%d\n",ans);
return 0;
}
/*
o
|
o
/ \
o o
o1
|
o2
/ | | \
o3 o4 o`5 o``6
/
o7
/ \
o8 o``9
9
1
2
2
2
2
4
7
7
*/
将军令是一个点可以覆盖与其相邻的k个点。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号