Tarjan

春有百花秋有月，夏有凉风冬有雪，若无闲事挂心头，便是人间好时节。  --《无门关》

解析：如果能没有忧思悲恐缠绕心田，那么每年每季每天都是人间最好的时节。

Tarjan讲解，时间戳和low[]

 

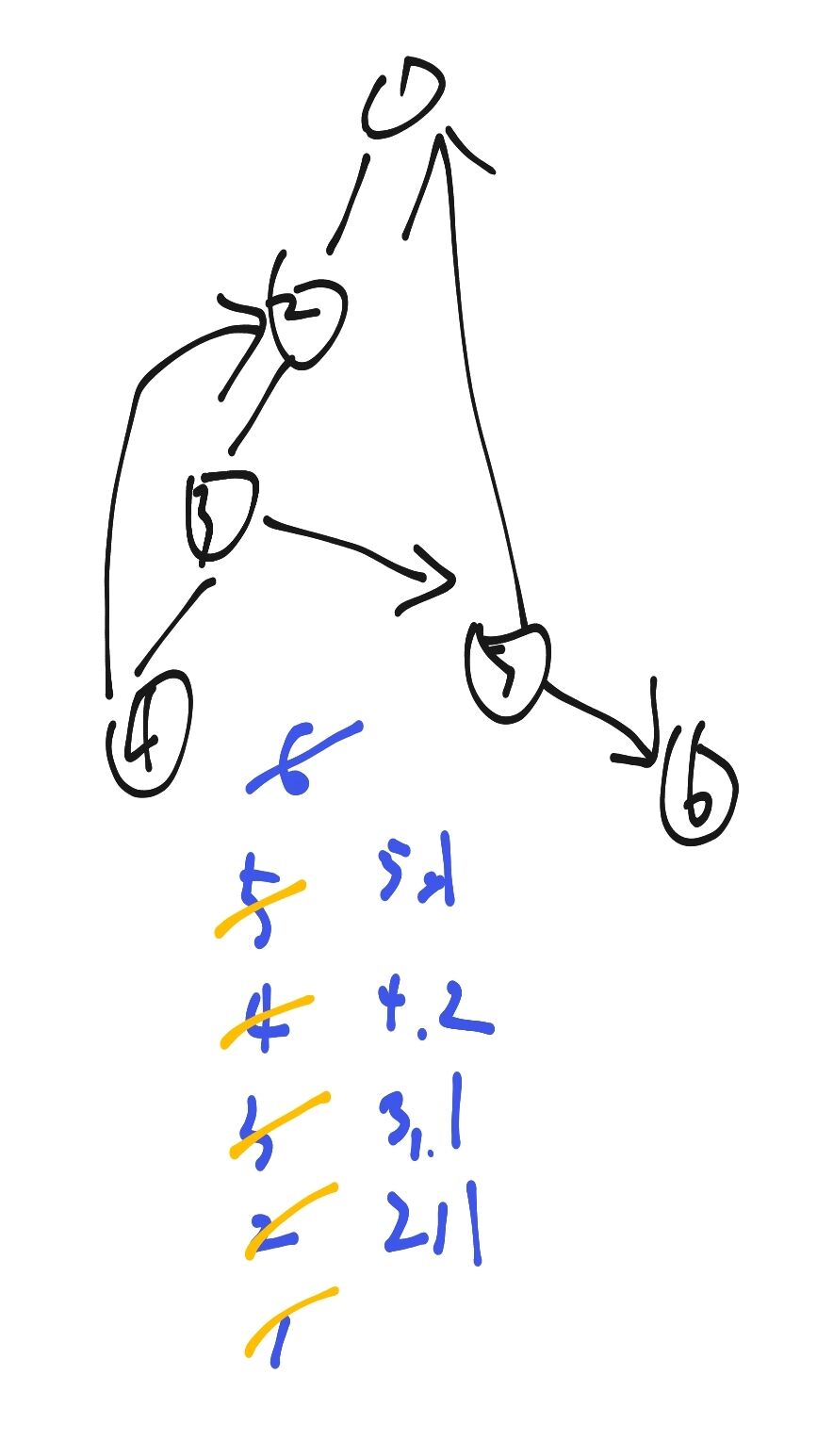
P2341(受欢迎的奶牛)

//统计出度为0的奶牛联通块
//如果出度为0的奶牛连通块不止一个，则没有一只奶牛为明星奶牛
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,x,y,cnt,tim,tp,scc_num,tot,hd[10005],dfn[10005],low[10005],stk[10005],vis[10005],blong[10005],num[10005],ot[10005];
struct Edge{
   int st,to,nxt;
}edge[50005];
void add(int u,int v){
  cnt++;
  edge[cnt].st = u;
  edge[cnt].to = v;
  edge[cnt].nxt = hd[u];
  hd[u] = cnt;
}
void tarjan(int u){
  dfn[u] = low[u] = ++tim;
  stk[++tp] = u;
  vis[u] = 1;    //是否在栈中，用来判断横叉边
  for(int i = hd[u]; i ; i = edge[i].nxt){
      int v = edge[i].to;
      if(!dfn[v]){ //如果没有被访问过
        tarjan(v);
          low[u] = min(low[u],low[v]);
      }
      else if(vis[v]){//如果被访问过了，则看是不是横叉边，如果是，则不处理，如果是返祖边，则更新
          low[u] = min(dfn[v],low[u]);
      }
  }//要访问完所有的边，从而确定当前点的最大强连通分量
  //如果当前点的所有边都访问完了，且其low == dfn 则说明他们子孙节点再也没有返祖的情况，则该栈中的点独立成为强连通分量了
  int tmp;
  if(low[u] == dfn[u]){
    scc_num++;
    do{
      tmp = stk[tp--];
      blong[tmp] = scc_num;
      vis[tmp] = 0;//出栈
      num[scc_num]++;//该强连通分量中有几个元素
    }while(tmp != u);
  }
}

int main(){
  scanf("%d%d",&n,&m);
  for(int i = 1; i <= m; i++){
    scanf("%d%d",&x,&y);
    add(x,y);
  }
  for(int i = 1; i <= n; i++){
    if(dfn[i] == 0){
      tarjan(i);
    }
  }
  for(int i = 1; i <= cnt; i++){
      if(blong[edge[i].st] != blong[edge[i].to]){
          ot[blong[edge[i].st]]++;
      }
  }
  int p;
  for(int i = 1; i <= scc_num; i++){
    if(ot[i] == 0)
      p = i, tot++;
  }
  if(tot == 1) printf("%d\n",num[p]);
  else printf("0\n");
  return 0;
}

 ### 割边

 

 

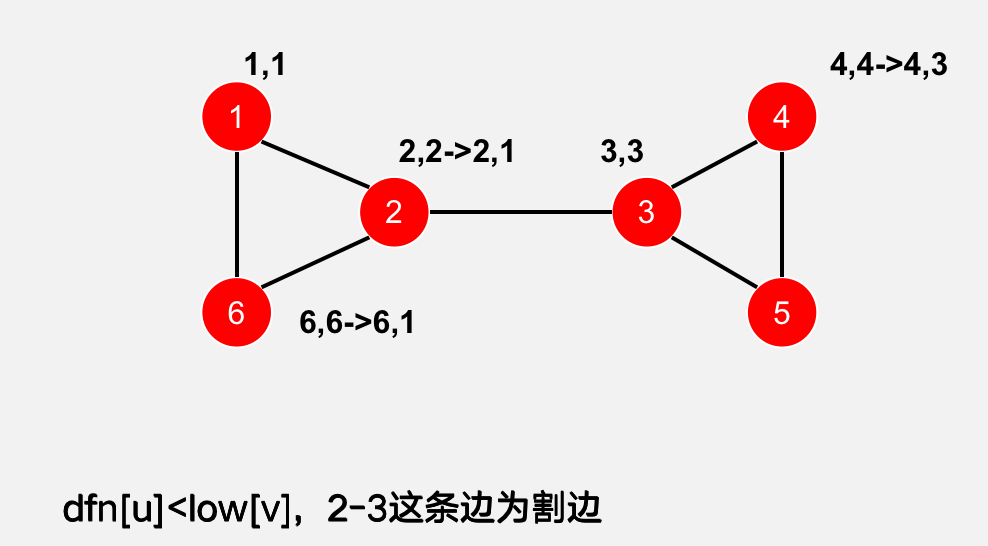
### 割点

P3469 [POI2008]BLO-Blockade

 

      对于非割点，答案显然是2(n-1) (因为它不能影响别的点对连通性，能影响的只是别人到它以及它到别人)

对于割点，它把那几块弄得无法联通，即那几块中不同块的两个点肯定就无法联通了，答案也就是每组块的点的数量互相乘出来t[1](n-t[1])+t[2](n-t[2])+......+t[a](n-t[a])+(n-1)+(1+sum)(n-sum-1)，最后再加上2(n-1)。

      一开始想不明白为什么(n-1)*1就要乘以2，但是t[1]*(n-t[1])就不用乘以2，原因在于遍历每一棵子树，如果x（子树）与y（另一个子树）一个数对，那么遍历到y子树，就会和x成一个数对。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000010;
inline int read()
{
    int x=0,t=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')t=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*t;
}
int n,m,head[maxn],num=0;
int dfn[maxn],low[maxn],size[maxn],tot=0;
long long ans[maxn];
bool cut[maxn];
struct node{
    int v,nex;
}e[maxn];
void add(int u,int v)
{
    e[++num].v=v;
    e[num].nex=head[u];
    head[u]=num;
}
void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    size[u]=1;
    int flag=0,sum=0;
    for(int i=head[u];i;i=e[i].nex)
    {
        int v=e[i].v;
        if(!dfn[v])
        {
            tarjan(v);
            size[u]+=size[v];
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                ans[u]+=(long long)size[v]*(n-size[v]);
                sum+=size[v];
                flag++;
                if(u!=1||flag>1) cut[u]=true;
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(!cut[u]) ans[u]=2*(n-1);
    else ans[u]+=(long long)(n-sum-1)*(sum+1)+(n-1);
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        int x,y;
        x=read(),y=read();
        add(x,y),add(y,x);
    }
    tarjan(1);
    for(int i=1;i<=n;i++) printf("%lld\n",ans[i]);
    return 0;
}

 

###P5022 旅行 2018年NOIP提高组day2t1

题目简意：n个点m条边的图，从1号城市开始访问其他城市，访问方法分两种，以选择一条与当前城市相连的道路，走向一个没有去过的城市，或者沿着第一次访问该 城市时经过的道路后退到上一个城市。在每到达一个新的城市时，将它的编号记录下来作为字典序。要求所有城市都访问过以后的最小字典序.

输入：  输出：1 3 2 5 4 6

6 5 
1 3 
2 3 
2 5 
3 4 
4 6

输入：   输出：1 3 2 4 5 6

6 6 
1 3 
2 3 
2 5 
3 4 
4 5 
4 6
说明：n<=5000,一部分数据是m = n-1, 另一部分是m=n

解析： 本题考查的是搜索+环的判定+细节处理。

代码1:是一棵树，可以发现访问一个点，必须将该点的子树都访问完再访问别的子树。如果访问该点后去访问其他子树，根据两种访问方式的要求，该点子树将无法再次访问。所有城市都访问的要求无法满足。因此，循环与该点相连的点，找到编号最小的进行访问，深搜后回溯。

/*
不存在两条连接同一对城市的道路，->没有重边
也不存在一条连接一个城市和它本身的道路。-> 没有自环
并且， 从任意一个城市出发，通过这些道路都可以到达任意一个其他城市。->一定连通
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdlib>
using namespace std;
int n,m,cnt,hd[5005],vis[5005],tot,f[5005],num[5005];
struct Edge{
    int to,nxt;
}edge[10000];//
void add(int u, int v){
    cnt++;
    edge[cnt].to = v;
    edge[cnt].nxt = hd[u];
    hd[u] = cnt;
    num[u]++;
}
int t ;
void dfs(int u){
    printf("%d ",u); int tot = 1;
    while(tot <= num[u]){
        int mv = n+1; tot++;
        for(int i = hd[u]; i ; i = edge[i].nxt){
            int v = edge[i].to;
            if(num[u]==1 && vis[v]) return;
            if(!vis[v] && v < mv) mv = v;
        }
        if(mv < n+1){//mv发生了变化
            vis[mv] = 1; dfs(mv);
        }
    }
}
int main(){
    scanf("%d%d",&n,&m); int x,y;
    for(int i = 1; i <= m; i++){
        scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    vis[1] = 1; dfs(1);
    return 0;
}

 

 代码2:n=m,只有一个环，我们发现在环上的路径可以转换为，断开环的一条边，然后再进行代码1的操作。因此可以先找环，然后循环断开。

断开边的时候注意因为是双向边，因此如果该边边号是奇数，那么对应双向边的另一条是奇数+1，如果是偶数，对应是偶数-1. 找环的方式是tarjan变形。

 

/*
不存在两条连接同一对城市的道路，->没有重边
也不存在一条连接一个城市和它本身的道路。-> 没有自环
并且， 从任意一个城市出发，通过这些道路都可以到达任意一个其他城市。->一定连通
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdlib>
#include<stack>
using namespace std;
int n,m,cnt,p,hd[5005],vis[5005],tot,num[5005],nm,res[5005],ans[5005],del[10005],dfn[5005],e[10005],low[5005],istack[5005];
stack<int> q;
struct Edge{
    int to,nxt,fr;
}edge[10005];//
void add(int u, int v){
    cnt++;
    edge[cnt].fr = u;
    edge[cnt].to = v;
    edge[cnt].nxt = hd[u];
    hd[u] = cnt;
    num[u]++;
}
void tarjan(int u,int fa){
    dfn[u] = ++tot; low[u] = tot;
    istack[u] = 1;
    q.push(u);
    for(int i = hd[u]; i; i = edge[i].nxt){
        int v = edge[i].to;
        if(!dfn[v]){
            tarjan(v,u);
            if(low[v] <= low[u] && v != fa){
                low[u] = low[v], e[++nm] = i;
            }
        }else if(istack[v]){
            if(dfn[v] < low[u] && v != fa){
                low[u] = dfn[v], e[++nm] = i;
            }
        }
    }
    if(low[u] == dfn[u]){
        int x;
        do{
            x = q.top(); q.pop(); istack[x] = 0;
        }while(low[x] != dfn[x]);
    }
}
int t ;
void dfs(int u){
    res[++p] = u; int tot = 1;
    while(tot <= num[u]){
        int mv = n+1; tot++;
        for(int i = hd[u]; i ; i = edge[i].nxt){
            int v = edge[i].to;
            if(del[i] || (num[u]==1 && vis[v])) continue;//rgt: return -> continue
            if(!vis[v] && v < mv) mv = v;
        }
        if(mv < n+1){//mv发生了变化
            vis[mv] = 1; dfs(mv);
        }
    }
}
void work(){
    // for(int i = 1; i<= n ;i++) printf("%d ",res[i]);
    // cout<<endl;
    for(int i = 1; i<= n; i++){
        if(res[i] > ans[i]) return;
        if(res[i] < ans[i]){
            for(int j = 1; j <= n; j++) {
                ans[j] = res[j];
            }
            break;
        }
    }
}
int main(){
    scanf("%d%d",&n,&m); int x,y;
    for(int i = 1; i <= m; i++){
        scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    if(m == n-1){
        vis[1] = 1; dfs(1);
        for(int i = 1; i <= n; i++)
            printf("%d ",res[i]);
    }else{
        tarjan(1,0);
        memset(ans,0x3f,sizeof ans);
        for(int i = 1; i <= nm; i++){//删除一条边以后，再跑dfs，之后怎么做？
            memset(del,0,sizeof del); p = 0;
            memset(vis,0,sizeof vis);

            del[e[i]] = 1; num[edge[e[i]].fr]--;
            if(e[i] % 2 == 1) del[e[i] + 1] = 1, num[edge[e[i] + 1].fr]--;
            else del[e[i]-1] = 1, num[edge[e[i]-1].fr]--;

            vis[1] = 1;    dfs(1);

            if(e[i] % 2 == 1) num[edge[e[i] + 1].fr]++;
            else num[edge[e[i]-1].fr]++;

            work();
        }
        for(int i = 1; i <= n; i++)
            printf("%d ",ans[i]);
    }
    return 0;
}
/*
3
1 3 4 5 2 6
6
1 3 2 4 5 6

1 3 2 5 4 6
*/

代码3:可以像网路流那样将边从2开始记录，这样双向边的两条边可以用抑或1来处理。

/*
不存在两条连接同一对城市的道路，->没有重边
也不存在一条连接一个城市和它本身的道路。-> 没有自环
并且， 从任意一个城市出发，通过这些道路都可以到达任意一个其他城市。->一定连通
*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdlib>
#include<stack>
using namespace std;
int n,m,cnt=1,p,hd[5005],vis[5005],tot,num[5005],nm,res[5005],ans[5005],del[10005],dfn[5005],e[10005],low[5005],istack[5005];
stack<int> q;
//2 ^ 1 = 10 ^ 1 = 11 , 11 ^ 1 = 10
struct Edge{
    int to,nxt,fr;
}edge[10005];//
void add(int u, int v){
    cnt++;
    edge[cnt].fr = u;
    edge[cnt].to = v;
    edge[cnt].nxt = hd[u];
    hd[u] = cnt;
    num[u]++;
}
void tarjan(int u,int fa){
    dfn[u] = ++tot; low[u] = tot;
    istack[u] = 1;
    q.push(u);
    for(int i = hd[u]; i; i = edge[i].nxt){
        int v = edge[i].to;
        if(!dfn[v]){
            tarjan(v,u);
            if(low[v] <= low[u] && v != fa){
                low[u] = low[v], e[++nm] = i;
            }
        }else if(istack[v]){
            if(dfn[v] < low[u] && v != fa){
                low[u] = dfn[v], e[++nm] = i;
            }
        }
    }
    if(low[u] == dfn[u]){
        int x;
        do{
            x = q.top(); q.pop(); istack[x] = 0;
        }while(low[x] != dfn[x]);
    }
}
int t ;
void dfs(int u){
    res[++p] = u; int tot = 1;
    while(tot <= num[u]){
        int mv = n+1; tot++;
        for(int i = hd[u]; i ; i = edge[i].nxt){
            int v = edge[i].to;
            if(del[i] || (num[u]==1 && vis[v])) continue;//rgt: return -> continue
            if(!vis[v] && v < mv) mv = v;
        }
        if(mv < n+1){//mv发生了变化
            vis[mv] = 1; dfs(mv);
        }
    }
}
void work(){
    // for(int i = 1; i<= n ;i++) printf("%d ",res[i]);
    // cout<<endl;
    for(int i = 1; i<= n; i++){
        if(res[i] > ans[i]) return;
        if(res[i] < ans[i]){
            for(int j = 1; j <= n; j++) {
                ans[j] = res[j];
            }
            break;
        }
    }
}
int main(){
    scanf("%d%d",&n,&m); int x,y;
    for(int i = 1; i <= m; i++){
        scanf("%d%d",&x,&y);
        add(x,y); add(y,x);
    }
    if(m == n-1){
        vis[1] = 1; dfs(1);
        for(int i = 1; i <= n; i++)
            printf("%d ",res[i]);
    }else{
        tarjan(1,0);
        memset(ans,0x3f,sizeof ans);
        for(int i = 1; i <= nm; i++){//删除一条边以后，再跑dfs，之后怎么做？
            memset(del,0,sizeof del); p = 0;
            memset(vis,0,sizeof vis);

            del[e[i]] = 1; num[edge[e[i]].fr]--;
            del[e[i] ^ 1] = 1, num[edge[e[i] ^ 1].fr]--;

            vis[1] = 1;    dfs(1);

            num[edge[e[i]].fr]++,num[edge[e[i] ^ 1].fr]++;
            work();
        }
        for(int i = 1; i <= n; i++)
            printf("%d ",ans[i]);
    }
    return 0;
}
/*
3
1 3 4 5 2 6
6
1 3 2 4 5 6

1 3 2 5 4 6
*/

 ### 点双 P3225 [HNOI2012]矿场搭建

 

/* 首先看到割点就是Tarjan搞 但是怎么搞

首先假设我们把所有的点双都缩点 那么我们一定可以得到一棵树 然后我们就会发现

1.叶子节点(只含有一个割点的点双)必须建 因为叶子节点如果不建 一旦割点被爆就死翘了

2.非叶节点(含有两个或两个以上的割点的点双)不用建 因为即使一个割点被爆了也可以沿着另一个割点走到一个叶节点

3.还有一种情况就是整个联通块都是点双(即不含割点的点双) 这样我们讨论点双的大小

如果只有一个点 那么这个点必须建 数据没有卡这个的点所以我没写(其实是我忘写了 然后还过了)

如果有两个或两个以上的点 那么要建两个 一个被爆了还可以走另一个

方案数就是乘法原理的问题了 注意叶节点那里出口不能建在割点上

所以先Tarjan求割点再dfs一下每个联通块就好了。

*/

*/
#include<iostream>#include<cstdio>#include<cstring>#define ll long longusing namespace std;int head[505],dfn[505],low[505],vis[505],stack[505];bool cut[505],in_stack[505];int n,m,cnt,num,tot,deg,ans1,T,cases,root,top;
ll ans2;struct node
{
    int from;
    int to;
    int next;
}e[1010];inline void first(){
    memset(head,0,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(cut,0,sizeof(cut));
    memset(vis,0,sizeof(vis));
    top=cnt=tot=n=ans1=T=0; ans2=1;
}inline void insert(int from,int to){
    e[++num].from=from;
    e[num].to=to;
    e[num].next=head[from];
    head[from]=num;
}inline int read(){
    int x=0,f=1; char c=getchar();
    while (c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while (c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}void Tarjan(int now,int father)//求割点 {
    dfn[now]=low[now]=++tot;
    for(int i=head[now];i;i=e[i].next)
        {
            int v=e[i].to;
            if(!dfn[v])
            {
                Tarjan(v,now);
                low[now]=min(low[now],low[v]);
                if(low[v]>=dfn[now])
                {
                    if(now==root) deg++;
                    else cut[now]=true;
                }
            }
            else if(v!=father) low[now]=min(low[now],dfn[v]);//不要跟求环混了 具体原理去网上找 
        }
}void dfs(int x)//遍历每个连通块 {
    vis[x]=T;//标记 
    if(cut[x]) return;
    cnt++;//数量 
    for(int i=head[x];i;i=e[i].next)
    {
        int v=e[i].to;
        if(cut[v]&&vis[v]!=T) num++,vis[v]=T;//统计割点数目。 
        //如果是割点且标记不与遍历的的连通块相同就修改标记。 
        if(!vis[v])dfs(v);
    }
}int main(){
    m=read();
    while (m)
    {
        first();
        for (int i=1;i<=m;i++)
        {
            int u=read(),v=read();
            n=max(n,max(u,v));//这个地方要处理一下 
            insert(u,v); insert(v,u);
        }
        for (int i=1;i<=n;i++)
        {
            if (!dfn[i]) Tarjan(root=i,0);
            if (deg>=2) cut[root]=1;//根节点的割点 
            deg=0;//不要忘记是多组数据 
        }
        for (int i=1;i<=n;i++)
            if (!vis[i]&&!cut[i])//不是割点 
            {
                T++; cnt=num=0;//T为连通块的标记 
                dfs(i);
                if (!num) ans1+=2,ans2*=cnt*(cnt-1)/2;//建两个 别忘记除以二 因为两个建立的出口没有差异 
                if (num==1) ans1++,ans2*=cnt;//建一个 
            }
        printf("Case %d: %d %lld\n",++cases,ans1,ans2);
        m=read();
    }
    return 0;
}