//1908逆序对
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<queue> using namespace std; #define ll long long const int mac=1e7+10; const int inf=1e9+5; struct node{ int l,r,sum; }tree[mac]; int sz=1;//动态分配的点的最大编号 ll query(int l,int r,int rt,int L,int R){ ll ans=0; if(!rt) return 0;//如果没有就返回0 if (l>=L && r<=R){ return tree[rt].sum; } int mid=(l+r)>>1; if (mid>=L) ans+=query(l,mid,tree[rt].l,L,R); if (mid<R) ans+=query(mid+1,r,tree[rt].r,L,R); return ans; } void update(int l,int r,int &rt,int pos) { if (!rt) rt = ++sz;//如果说这个节点不存在,我们就将节点数+1,当前节点为最大最大节点,和主席树有点类似,而这也是动态开点的核心 if (l==r) { tree[rt].sum++; return; } int mid=(l+r)>>1; if (mid>=pos) update(l,mid,tree[rt].l,pos);//注意这里传进去的rt是左儿子的编号 else update(mid+1,r,tree[rt].r,pos); tree[rt].sum=tree[tree[rt].l].sum+tree[tree[rt].r].sum; } int main(){ int n; scanf ("%d",&n); ll ans=0; int root=1; for (int i=1; i<=n; i++){ int x; scanf ("%d",&x); ans+=query(1,inf,1,x+1,inf); update(1,inf,root,x); } printf ("%lld\n",ans); return 0; }
以下这段代码包含了建树的过程,合并在update中
#include<bits/stdc++.h> #define ll long long #define N 2000005 using namespace std; int tot, n, x, mx, root, a[N], b[N]; ll sum; struct Node{ int l, r, cnt, p, q; }tr[N]; void pushup(int rt){ tr[rt].cnt = tr[tr[rt].l].cnt + tr[tr[rt].r].cnt; } void update(int l, int r, int &rt, int x){ if(rt == 0){ rt = ++tot; tr[rt].p = l, tr[rt].q = r; } if(l == r){ tr[rt].cnt++;//不止有一个 return; } int mid = (l+r)>>1; if(x <= mid) update(l, mid, tr[rt].l, x); else update(mid+1, r, tr[rt].r, x); pushup(rt); } ll query(int rt, int L, int R){ if(!rt) return 0ll; if(L <= tr[rt].p && R >= tr[rt].q){ return tr[rt].cnt + 0ll; } int mid = (tr[rt].p + tr[rt].q)>>1; ll ans = 0; if(L <= mid) ans = query(tr[rt].l, L ,R); if(R > mid) ans += query(tr[rt].r, L, R); return ans; } int main(){ cin>>n; for(int i = 1; i <= n; i++){ cin>>a[i]; b[i] = a[i]; } sort(b+1, b+n+1); mx = b[n]; int k = unique(b+1, b+n+1) - (b+1); for(int i = 1; i <= n; i++){ int x = lower_bound(b+1, b+k+1, a[i]) - b; update(1, mx, root, x); // cout<<"x: "<<x<<" "<<query(1, mx, 1, x+1, mx)<<endl; sum += query(1, x+1, mx); } // cout<<tr[4].cnt<<endl; // cout<<"tr: "<<tr[1].p<<" "<<tr[1].q<<" "<<tr[1].cnt<<endl; // cout<<"tr: "<<tr[1].p<<" "<<tr[1].q<<" "<<tr[2].cnt<<endl; cout<<sum<<endl; return 0; } /* 3 4 1 2 1-5(1) 1-3(4) 4-5(2) 1-2(5) x x 4-4(3) 1-1(6) 2-2(7) */
雨天的尾巴
简化题意后:1.只有一种救济粮,对于序列而言,将x-y之间的点,都发这一种救济粮,那么题目就是一个简单的差分前缀和。
2.如果不止有一种救济粮,则可以将每个点都开一个以种类为序号的线段树,然后线段树从前向后合并。同时维护每种救济粮个数的最大值及种类。
3.对于一棵树而言,前缀和的操作就是自下而上线段树合并的过程。
树上点差分,是自下而上来做,一条链的底端两个节点值+x,lca处的节点-x。这样自底而上对做前缀和,在树上就是线段树合并了。
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #define mxn 100005 #define M 10000005 using namespace std; int n,m,R,dep[mxn],f[mxn],size[mxn],cnt,hd[mxn],son[mxn],tp[mxn],ans[mxn]; int d[M],t[M],l[M],rt[M],r[M]; int tot; struct Edge{ int nxt, to; }edge[200005]; void add(int u, int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void dfs1(int u, int fa){ int mx = -1; size[u] = 1; for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dep[v] = dep[u] + 1; f[v] = u; dfs1(v, u); size[u] += size[v]; if(size[v] > mx){ mx = size[v], son[u] = v; } } } void dfs2(int u, int top, int fa){ tp[u] = top; if(son[u]) dfs2(son[u], tp[u], u); for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; if(v != son[u]) dfs2(v, v, u); } } int LCA(int x, int y){ while(tp[x] != tp[y]){ if(dep[tp[x]] < dep[tp[y]]) swap(x,y); x = f[tp[x]]; } if(dep[x] < dep[y]) return x; else return y; } void pushup(int rt){ if(d[l[rt]] >= d[r[rt]]){// d[rt] = d[l[rt]], t[rt] = t[l[rt]]; }else{ d[rt] = d[r[rt]], t[rt] = t[r[rt]]; } } void change(int &rt, int x, int y, int pos, int val){ if(!rt) rt = ++tot;//动态开点 if(x == y){ d[rt] += val; t[rt] = x; return; } int mid = (x+y)>>1; if(pos <= mid) change(l[rt], x, mid, pos, val); else change(r[rt], mid+1, y, pos, val); pushup(rt); } void merge(int &u, int v, int x, int y){ if(!u){//只有一棵线段树,u为空 u = v; return; } if(!v) return;//v为空,直接返回 if(x == y){ d[u] += d[v]; t[u] = x; return;// } int mid = (x+y)>>1; merge(l[u], l[v], x, mid); merge(r[u], r[v], mid+1, y); pushup(u); } void dfs(int u){ for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(dep[v] > dep[u]) dfs(v), merge(rt[u], rt[v], 1, R);//少dfs(v) } if(d[rt[u]]) ans[u] = t[rt[u]]; } int main(){ int xx,yy,zz,x[mxn],y[mxn],z[mxn]; scanf("%d%d",&n,&m); for(int i = 1; i <= n-1; i++){ scanf("%d%d",&xx,&yy); add(xx,yy); add(yy,xx); } dep[1] = 1; dfs1(1,0); dfs2(1,1,1); for(int i = 1; i <= m; i++){ scanf("%d%d%d",&x[i],&y[i],&z[i]); R = max(R, z[i]); } for(int i = 1; i <= m; i++){ int lca = LCA(x[i], y[i]); // cout<<lca<<" "; change(rt[x[i]], 1, R, z[i], 1); change(rt[y[i]], 1, R, z[i], 1); change(rt[lca], 1, R, z[i], -1);//少rt[] if(f[lca]) change(rt[f[lca]], 1, R, z[i], -1);//少rt } // cout<<t[1]<<endl; dfs(1); for(int i = 1; i <= n; i++) printf("%d\n",ans[i]); return 0; }
CF1009F Dominant Indices
给定一棵以 1 为根,n个节点的树。设 d(u,x) 为 u 子树中到 u 距离为 x 的节点数。对于每个点,求一个最小的 k,使得 d(u,k)最大。
#include<bits/stdc++.h>
#define N 1000005
#define M 21000005
using namespace std;
int CNT, n, dep[N], rt[N], hd[N], cnt, ans[N];
struct Edge{
int nxt, to;
}edge[2*N];
void add(int u, int v){
edge[++cnt].to = v;
edge[cnt].nxt = hd[u];
hd[u] = cnt;
}
struct Node{
int l, r, val, id;
}tr[M];
void pushup(int u){
int l = tr[u].l, r = tr[u].r;
if(tr[l].val >= tr[r].val){
tr[u].val = tr[l].val, tr[u].id = tr[l].id;
}
else {
tr[u].val = tr[r].val, tr[u].id = tr[r].id;
}
}
void insert(int &now, int l, int r, int x, int val){
if(!now) now = ++CNT;
if(l == r){
tr[now].val += val;//这个可以不累加 tr[now].val = val;
tr[now].id = x;
return;
}
int mid = (l + r) >> 1;
if(x <= mid) insert(tr[now].l, l, mid, x, val);
else insert(tr[now].r, mid+1, r, x, val);
pushup(now);
}
void merge(int &x, int y, int l, int r){
if(!x) {x = y; return;}
if(!y) return;
if(l == r){
tr[x].val += tr[y].val;
//tr[x].id = l;//深度不变
return;
}
int mid = (l+r)>>1;
merge(tr[x].l, tr[y].l, l, mid);
merge(tr[x].r, tr[y].r, mid+1, r);
pushup(x);
}
void dfs(int u, int fa){
dep[u] = dep[fa]+1;
insert(rt[u], 1, n, dep[u], 1);
for(int i = hd[u]; i; i = edge[i].nxt){
int v = edge[i].to;
if(v == fa) continue;
dfs(v, u);
merge(rt[u], rt[v], 1, n);
}
ans[u] = tr[rt[u]].id - dep[u];
}
int main(){
scanf("%d",&n); int x, y;
for(int i = 1; i <= n-1; i++){
scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
dfs(1, 0);
for(int i = 1; i <= n; i++){
printf("%d\n",ans[i]);
}
return 0;
}
下面是错误的代码及代码错误处
#include<cstdio> #include<iostream> #include<cmath> #include<algorithm> #include<cstring> #define mxn 1000005 using namespace std; int n, cnt, hd[mxn], dep[mxn], root[mxn*21], ans[mxn], CNT;//21是log长度 struct Edge {int to,nxt;} edge[mxn*2]; struct Tree {int l,r,val,id;} tr[mxn*21]; void add(int u, int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void pushup(int u){ tr[tr[u].l].val >= tr[tr[u].r].val ? tr[u].val = tr[tr[u].l].val, tr[u].id = tr[tr[u].l].id : tr[u].val = tr[tr[u].r].val, tr[u].id = tr[tr[u].r].id;
// x > y ? a = 1, b = 2 : c = 3, d = 4;
//这句话的意思是 x>y? a=1,b=2:c=3 并且 d=4
} void insert(int &now, int l, int r, int dep, int val){ if(!now) now++; // now = ++CNT if(l == r){ tr[now].val += val; tr[now].id = dep; return; } int mid = (l + r)>>1; if(dep <= mid) insert(tr[now].l, l, mid, dep, val); else insert(tr[now].r, mid+1, r, dep, val); pushup(now); } void merge(int &u, int v, int l, int r){ if(!u) {u = v; return;} if(!v) return; if(l == r){ tr[u].val += tr[v].val, tr[u].id = l; return; } int mid = (l+r)>>1; merge(tr[u].l, tr[v].l, l, mid); merge(tr[u].r, tr[v].r, mid+1, r); pushup(u); } void dfs(int u, int fa){ dep[u] = dep[fa] + 1; insert(root[u], 1, n, dep[u], 1); for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dfs(v, u); merge(root[u], root[v], 1, n); } ans[u] = tr[root[u]].id - dep[u]; } int main(){ int x,y; scanf("%d",&n); for(int i = 1; i <= n-1; i++){ scanf("%d%d",&x,&y); add(x,y); add(y,x); } dfs(1,0); for(int i = 1; i <= n; i++) printf("%d\n",ans[i]); return 0; }
小Z学了逆序对以后想考考大家,于是他画了一棵有n个叶子节点的二叉树,在每个叶子节点标记一个n以内的权值ai,使得每个叶节点的权值不重复。并且树的非叶节点都存在两个儿子,你可以将一个节点上的两棵子树交换,使得这颗树的先序遍历中叶节点组成的序列中逆序对数量最少。
输入:
第一行n
下面每行,一个数x
如果x==0,表示这个节点非叶子节点,递归地向下读入左右儿子信息,
如果x!=0,表示这个节点是叶子节点,权值为x
输出:
一行,最少逆序对个数
输入样例:
3
0
0
3
1
2
输出样例:
1
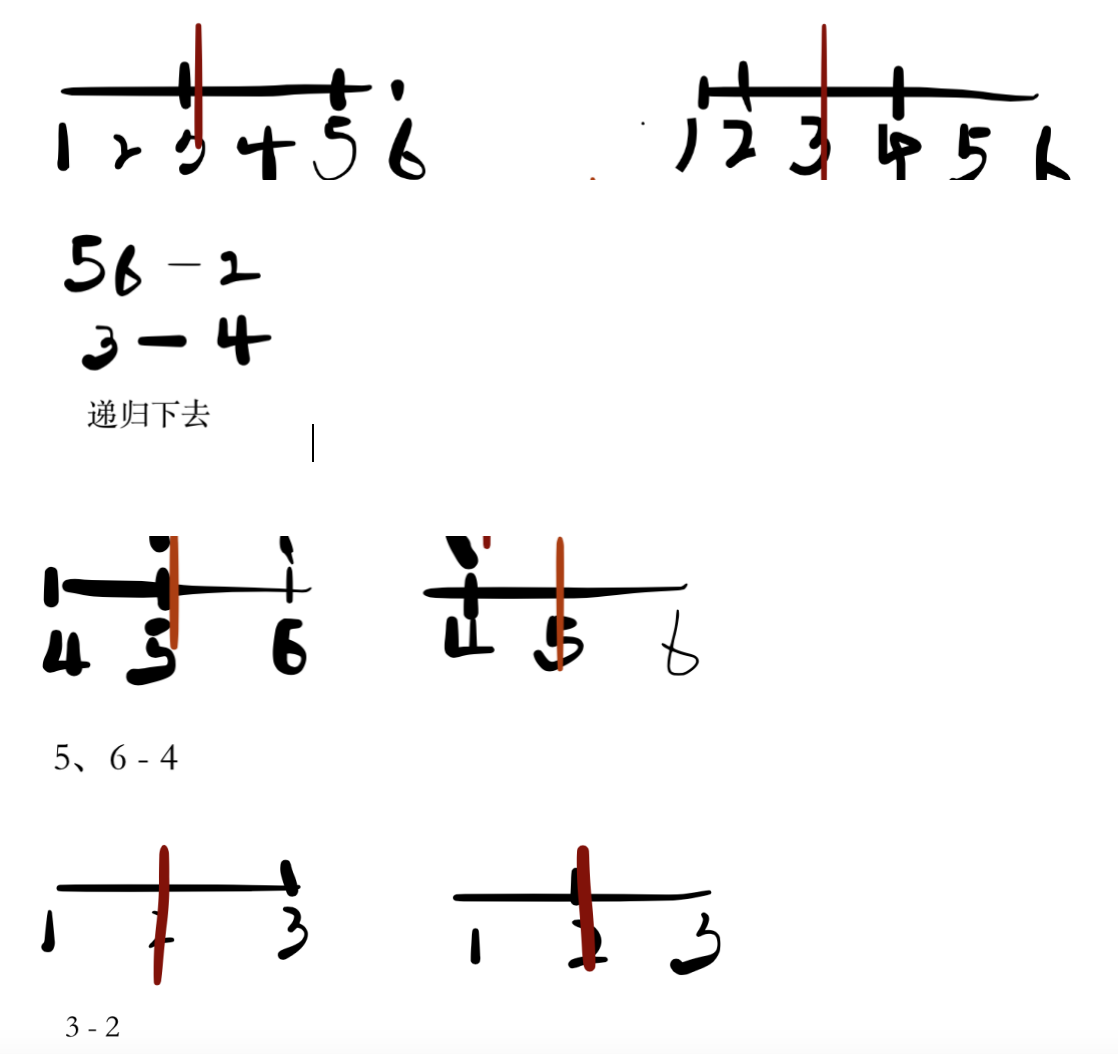
交换左右子树,只是这个节点的直接子树交换才对这个节点的逆序对数有影响。
每个节点的逆序对是左子树的逆序对的数量+右子树的逆序对数量+左子树对右子树的影响。
左子树对右子树的影响:右子树(l,mid)*左子树(mid+1,r)即为影响。
对两个子树建立权值线段树。不交换ans1 = cnt左[rs]*cnt右[ls],交换ans2cnt左[ls]*cnt右[rs]。
ans1,ans2取较小值作为此节点的贡献,这样自底向上合并就可以了。
#include<bits/stdc++.h> #define ll long long using namespace std; const int N = 2e5 + 5; ll lans, rans, ans; int n, CNT; struct Tree{ int l, r, val; }tr[N*19]; void pushup(int rt){ tr[rt].val = tr[tr[rt].l].val + tr[tr[rt].r].val; } void update(int &now, int l, int r, int pos){ now = ++CNT; if(l == r){ tr[now].val = 1; return; } int mid = (l+r)>>1; if(pos <= mid) update(tr[now].l, l, mid, pos); else update(tr[now].r, mid+1, r, pos); pushup(now); } void merge(int &x, int y, int l, int r){ if(!y) return; if(!x) { x = y; return; } if(l == r){ tr[x].val += tr[y].val; return; } lans += 1ll * tr[tr[x].r].val * tr[tr[y].l].val; rans += 1ll * tr[tr[x].l].val * tr[tr[y].r].val; int mid = (l+r)>>1; merge(tr[x].l, tr[y].l, l, r); merge(tr[x].r, tr[y].r, l, r); pushup(x); } int dfs(){ int rt, x, ls, rs; scanf("%d",&x); if(x) update(rt, 1, n, x);//叶子节点才新建立一课线段树 else{ ls = dfs(), rs = dfs();//两个两个是一对 lans = rans = 0; merge(ls, rs, 1, n); rt = ls; ans += min(lans, rans); } return rt; } int main(){ scanf("%d",&n); dfs(); printf("%lld\n", ans); return 0; }
树上数颜色
https://www.luogu.com.cn/problem/U41492
解析:无良商家,居然颜色超过n,或者为负数。只能离散化。更一般的代码看下一个代码。
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int const N = 1e5+5; int cnt,hd[N],CNT,rt[N],n,ans[N],c[N],t,b[N]; struct Edge{ int to,nxt; }edge[N*2]; void add(int u, int v){ edge[++cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } struct Tree{ int l, r, val; }tr[N*22]; void pushup(int u){ tr[u].val = tr[tr[u].l].val + tr[tr[u].r].val; } void update(int &now, int l, int r, int pos){ if(!now) now = ++CNT; if(l == r){ tr[now].val = 1; return; } int mid = (l+r)>>1; if(pos <= mid) update(tr[now].l, l, mid, pos); else update(tr[now].r, mid+1, r, pos); pushup(now); } void merge(int &x, int y, int l, int r){ if(!y) return; if(!x){ x = y; return; } if(l == r){ tr[x].val |= tr[y].val; return; } int mid = (l+r)>>1; merge(tr[x].l, tr[y].l, l, mid); merge(tr[x].r, tr[y].r, mid+1, r); pushup(x); } void dfs(int u, int fa){ for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dfs(v, u); merge(rt[u], rt[v], 1, n); } ans[u] = tr[rt[u]].val; } int main(){ scanf("%d",&n); int x,y,m,z; for(int i = 1; i <= n-1; i++){ scanf("%d%d",&x,&y); add(x,y); add(y,x); } for(int i = 1; i <= n; i++){ scanf("%d",&c[i]); b[i] = c[i]; } sort(b+1, b+n+1); int p = unique(b+1, b+n+1) - (b+1); for(int i = 1; i <= n; i++){ t = lower_bound(b+1, b+p+1, c[i]) - b; update(rt[i], 1, n, t); } dfs(1, 0); scanf("%d",&m); for(int i = 1; i <= m; i++){ scanf("%d",&z); printf("%d\n",ans[z]); } return 0; }
#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> using namespace std; int const N = 1e5+5; int cnt,hd[N],CNT,rt[N],n,ans[N]; struct Edge{ int to,nxt; }edge[N*2]; void add(int u, int v){ edge[++cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } struct Tree{ int l, r, val; }tr[N*19]; void pushup(int u){ tr[u].val = tr[tr[u].l].val + tr[tr[u].r].val; } void update(int &now, int l, int r, int pos){ if(!now) now = ++CNT; if(l == r){ tr[now].val = 1; return; } int mid = (l+r)>>1; if(pos <= mid) update(tr[now].l, l, mid, pos); else update(tr[now].r, mid+1, r, pos); pushup(now); } void merge(int &x, int y, int l, int r){ if(!y) return; if(!x){ x = y; return; } if(l == r){ tr[x].val |= tr[y].val; return; } int mid = (l+r)>>1; merge(tr[x].l, tr[y].l, l, mid); merge(tr[x].r, tr[y].r, mid+1, r); pushup(x); } void dfs(int u, int fa){ for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dfs(v, u); merge(rt[u], rt[v], 1, n); } ans[u] = tr[rt[u]].val; } int main(){ scanf("%d",&n); int x,y,m,z; for(int i = 1; i <= n-1; i++){ scanf("%d%d",&x,&y); add(x,y); add(y,x); } for(int i = 1; i <= n; i++){ scanf("%d",&z); update(rt[i], 1, n, z); } dfs(1, 0); scanf("%d",&m); for(int i = 1; i <= m; i++){ scanf("%d",&z); printf("%d\n",ans[z]); } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号