昨夜雨疏风骤,浓睡不消残酒,试问卷帘人,却道海棠依旧。知否知否,应是绿肥红瘦。 --《如梦令》
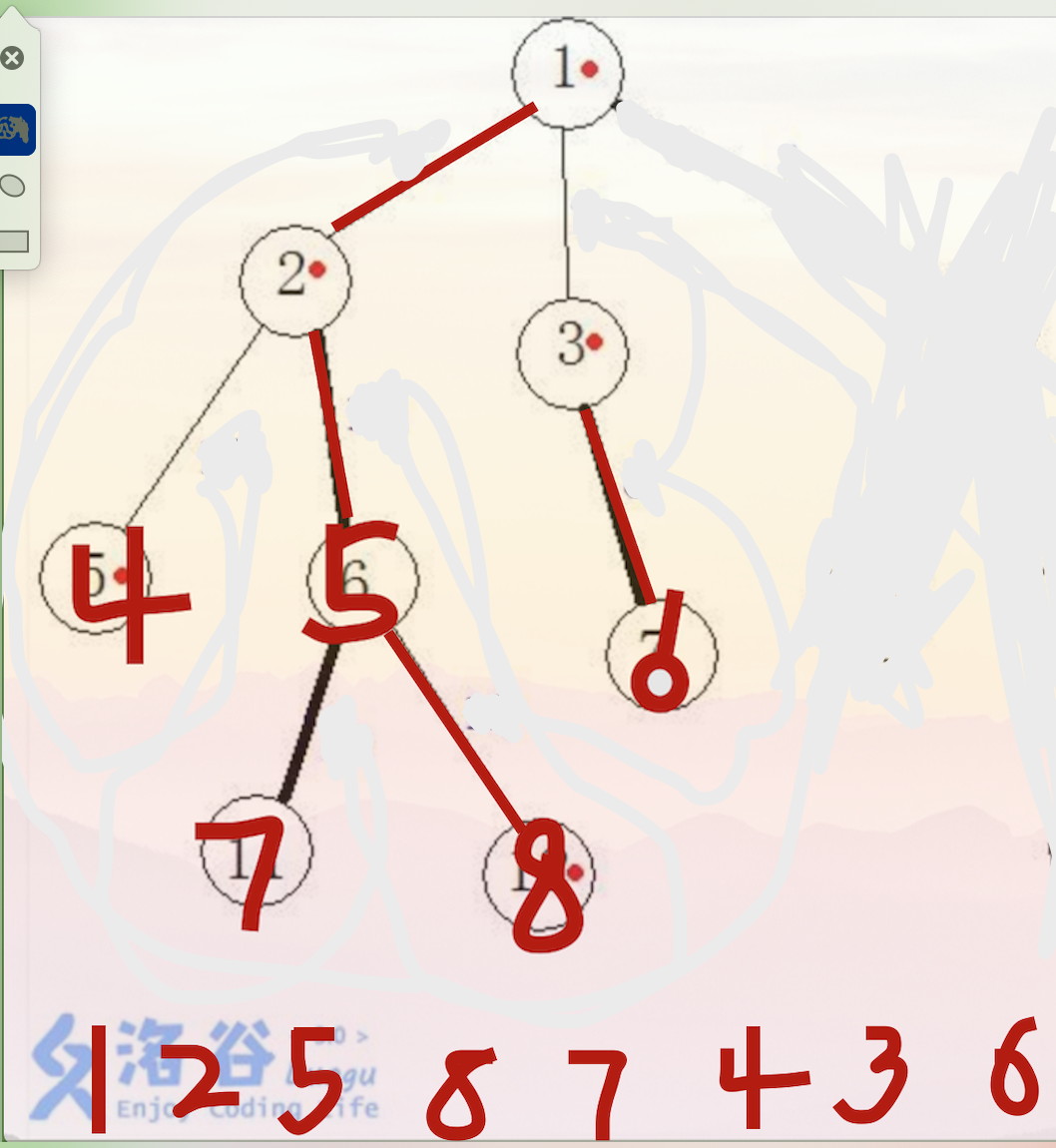
O 树链剖分的本质是把一棵树映射到线段上,且树被剖出来的链是连续的一段。看下图:

树剖的方法是先剖重的,这样dfs,并记录时间戳,也就是dfs序的序号。上图映射到线段上就是:

其中加括号的区间是重链部分。
O 那么这样做有什么好处?
比如我们要将树上某一路径x到y(比如7点-13点)上的点权值都+z,可以转化为在序列上进行。方法是:首先判断两个点的top[]是否相同,如果相同说明就在一个重链上,直接用线段树去处理。如若不然,判断dep(top[7])和dep(top[13]),即两个点的top[]值的深度。深的为7,浅的是13,那么先计算7-top[7],将该区间+z,区间更新使用线段树。走到top[7]后,将x = fa[top[7]],跳到1号点。重复判断两个点的top[]是否相同,如果不相同,继续判断dep[top[x]]和dep[top[13]],以此类推。
可以看出树上的问题转到序列上就是处理区间[8,9],[1,4]的问题,使用线段树即可。
O 又如将x(例如4)的子树节点权值都+z,在序列上就是区间[2,6]的区域。我们可以在 dfs过程中记录子树大小size[x],那么就用线段树处理学序列上的区间[x,x+size[x]-1]了。
O 其余的树链剖分方法看博客:
https://www.cnblogs.com/ivanovcraft/p/9019090.html
1.写回顾了一下线段树的单点修改,区间查询和与最大值:
洛谷2590浙江OI2008树的统计:
输入:
4
1 2 2 3 4 1 4 2 1 3
5
QMAX 1 3
QSUM 2 3
CHANGE 2 5
QMAX 1 3
QSUM 2 3
输出:
4
3
5
6

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; typedef long long LL; int const MXN=100005; char str[10]; int n, w[3*10000+5],x,y,cnt,hd[3*10000+5],q; struct Tree{ int l,r,sum,mx; }tree[12*10000]; struct Edge{ int to,nxt; }edge[6*10000+5]; void add(int u,int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void pushup(int rt){ tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum; tree[rt].mx = max(tree[rt<<1].mx, tree[rt<<1|1].mx); } void build(int rt,int L,int R){ tree[rt].l = L; tree[rt].r = R; if(L == R){ tree[rt].sum = w[L];//写成了小写w[l] tree[rt].mx = w[L]; return ; } int mid = (L+R)>>1; build(rt<<1,L,mid); build(rt<<1|1,mid+1,R); pushup(rt); } void change(int rt,int L,int t){ if(L < tree[rt].l || L >tree[rt].r) return; if(tree[rt].l == tree[rt].r){ tree[rt].sum = t; tree[rt].mx = t; return; } int mid = (tree[rt].l + tree[rt].r)>>1; if(L <= mid) change(rt<<1,L,t); else change(rt<<1|1,L,t); pushup(rt); } int querymax(int rt, int L ,int R){ if(L <= tree[rt].l && R >= tree[rt].r){//err: L >=... R<=.. return tree[rt].mx; } int mid = (tree[rt].l + tree[rt].r)>>1; int tmp = -0x7fffffff; if(L <= mid) tmp = max(tmp,querymax(rt<<1,L,R)); if(R >= mid+1)//err:else tmp = max(tmp,querymax(rt<<1|1,L,R)); return tmp; } int querysum(int rt, int L, int R){ if(L <= tree[rt].l && R >= tree[rt].r){ return tree[rt].sum; } int mid = (tree[rt].l + tree[rt].r)>>1; int sum = 0; if(L <= mid) sum += querysum(rt<<1,L,R); if(R >= mid+1) sum += querysum(rt<<1|1,L,R); return sum; } int main(){ scanf("%d",&n); for(int i=1;i<=n-1;i++){ scanf("%d%d",&x,&y); add(x,y);add(y,x); } for(int i=1;i<=n;i++) scanf("%d",&w[i]); build(1,1,n); scanf("%d",&q); int l,r; for(int i = 1; i <= q; i++){ scanf("%s%d%d",str,&l,&r); if(str[1]=='H'){ change(1,l,r); }else if(str[1]=='M'){ printf("%d\n",querymax(1,l,r)); }else if(str[1]=='S'){ printf("%d\n", querysum(1,l,r)); } } }
完整代码如下:

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> using namespace std; typedef long long LL; char str[10]; int n, w[300005],x,y,cnt,hd[300005],q,size[300005],son[300005],dfn,id[300005],a[300005],tp[300005]; int dep[300005],fa[300005]; struct Tree{ int l,r,sum,mx; }tree[12*10000]; struct Edge{ int to,nxt; }edge[6*10000+5]; void add(int u,int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void dfs1(int u,int f){//第一步,主要求出son[] size[u] = 1; int mx = 0; for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(f == v) continue; fa[v] = u; dep[v] = dep[u] + 1; dfs1(v,u); if(size[v] > mx){ mx = size[v]; son[u] = v; } size[u] += size[v]; } } void dfs2(int u,int f){//第二步,主要将树映射到序列上 ++dfn; a[dfn] = w[u];//a[1] a[2]... id[u] = dfn; if(son[u]){ tp[son[u]] = tp[u]; dfs2(son[u],u); } for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == f) continue; if(v != son[u]){ tp[v] = v; dfs2(v,u); } } } void pushup(int rt){ tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum; tree[rt].mx = max(tree[rt<<1].mx, tree[rt<<1|1].mx); } void build(int rt,int L,int R){ tree[rt].l = L; tree[rt].r = R; if(L == R){ tree[rt].sum = a[L];//写成了小写w[l] tree[rt].mx = a[L]; return ; } int mid = (L+R)>>1; build(rt<<1,L,mid); build(rt<<1|1,mid+1,R); pushup(rt); } void change(int rt,int L,int t){ if(L < tree[rt].l || L >tree[rt].r) return; if(tree[rt].l == tree[rt].r){ tree[rt].sum = t; tree[rt].mx = t; return; } int mid = (tree[rt].l + tree[rt].r)>>1; if(L <= mid) change(rt<<1,L,t); else change(rt<<1|1,L,t); pushup(rt); } int querymax(int rt, int L ,int R){ if(L <= tree[rt].l && R >= tree[rt].r){//err: L >=... R<=.. return tree[rt].mx; } int mid = (tree[rt].l + tree[rt].r)>>1; int tmp = -0x7fffffff; if(L <= mid) tmp = max(tmp,querymax(rt<<1,L,R)); if(R >= mid+1)//err:else tmp = max(tmp,querymax(rt<<1|1,L,R)); return tmp; } int querysum(int rt, int L, int R){ if(L <= tree[rt].l && R >= tree[rt].r){ return tree[rt].sum; } int mid = (tree[rt].l + tree[rt].r)>>1; int sum = 0; if(L <= mid) sum += querysum(rt<<1,L,R); if(R >= mid+1) sum += querysum(rt<<1|1,L,R); return sum; } int main(){ scanf("%d",&n); for(int i=1;i<=n-1;i++){ scanf("%d%d",&x,&y); add(x,y);add(y,x); } for(int i=1;i<=n;i++) scanf("%d",&w[i]); dep[1] = 1; dfs1(1,0); tp[1] = 1; dfs2(1,0); // for(int i = 1; i <= n; i++) // cout<<i<<" "<<dep[i]<<" "<<tp[i]<<endl; build(1,1,n); // cout<<querymax(1,6,6)<<endl; scanf("%d",&q); int l,r; for(int i = 1; i <= q; i++){ scanf("%s%d%d",str,&l,&r); if(str[1]=='H'){ change(1,id[l],r); }else if(str[1]=='M'){ // printf("%d\n",querymax(1,l,r)); int mx = -0x7fffffff; while(tp[l] != tp[r]){ if(dep[tp[l]] < dep[tp[r]]) swap(l,r); // cout<<l<<" "<<tp[l]<<" "<<r<<" "<<tp[r]<<endl; // cout<<id[l]<<" "<<id[tp[l]]<<endl; mx = max(mx,querymax(1,id[tp[l]],id[l]));//err:深的在左 // cout<<"mx:"<<mx<<endl; l = fa[tp[l]]; } // cout<<l<<" "<<r<<endl; if(dep[l] > dep[r]) swap(l,r); // cout<<dep[l]<<" "<<dep[r]<<endl; mx = max(mx,querymax(1,id[l],id[r]));//err:深的在左边 printf("%d\n",mx); }else if(str[1]=='S'){ // printf("%d\n", querysum(1,l,r)); int sum = 0; while(tp[l] != tp[r]){ if(dep[tp[l]] < dep[tp[r]]) swap(l,r); sum += querysum(1,id[tp[l]],id[l]); l = fa[tp[l]]; } if(dep[l] > dep[r]) swap(l,r); sum += querysum(1,id[l],id[r]); printf("%d\n",sum); } } } /* 8 1 2 1 3 2 4 2 5 3 6 5 7 5 8 1 2 3 4 5 6 7 8 3 QMAX 4 8 CHANGE 5 10 QMAX 4 8 */
P2146软件包管理系统
题解:一开始将所有数据都置1,flag=-1,如果安装就变成0,卸载就变成1。如果安装则计算从0到该节点的和,如果卸载就计算子树大小-子树的和就是需要卸载的软件个数。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
int n,x,m,a[100005],cnt,hd[100005],dfn,id[100005],size[100005],son[100005],tp[100005],fa[100005];
char str[15];
struct Edge{
int to,nxt;
}edge[100005];
void add(int u,int v){
cnt++;
edge[cnt].to = v;
edge[cnt].nxt = hd[u];
hd[u] = cnt;
}
struct Tree{
int l,r,sum,one;
}tree[400005];
//0表示已经安装的,1表示没有安装的
void dfs1(int u){
size[u] = 1;
int mx = 0;
for(int i = hd[u]; i; i = edge[i].nxt){
int v = edge[i].to;
fa[v] = u;
dfs1(v);
if(size[v] > mx){
mx = size[v];
son[u] = v;
}
size[u] += size[v];
}
}
void dfs2(int u){
dfn++;
a[dfn] = 1;
id[u] = dfn;
if(son[u]){
tp[son[u]] = tp[u];
dfs2(son[u]);
}
for(int i = hd[u]; i ; i = edge[i].nxt){
int v = edge[i].to;
if(son[u] != v){
tp[v] = v;
dfs2(v);
}
}
}
void pushup(int rt){
tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
// tree[rt].one = tree[rt<<1].one || tree[rt<<1|1].one;
}
void pushdown(int rt){//标记下放不仅下放标记,还有sum值
int one = tree[rt].one ;
if(one != -1){
tree[rt<<1].one = one;
tree[rt<<1].sum = (tree[rt<<1].r - tree[rt<<1].l + 1) * one;
tree[rt<<1|1].one = one;
tree[rt<<1|1].sum = (tree[rt<<1|1].r - tree[rt<<1|1].l + 1) * one;
tree[rt].one = -1;
}
}
void build(int rt, int L, int R){
tree[rt].l = L, tree[rt].r = R;
tree[rt].one = -1;//
if(L == R){
tree[rt].sum = a[L];
return ;
}
int mid = (tree[rt].l + tree[rt].r)>>1;
build(rt<<1,L,mid);
build(rt<<1|1,mid+1,R);
pushup(rt);
}
void update(int rt,int L,int R,int t){//改变就要上升
if(L <= tree[rt].l && R >= tree[rt].r){
tree[rt].sum = t * (tree[rt].r - tree[rt].l + 1);
tree[rt].one = t;
return;
}
if(tree[rt].one != -1)pushdown(rt);
int mid = (tree[rt].l + tree[rt].r)>>1;
if(L <= mid)
update(rt<<1,L,R,t);
if(R > mid)
update(rt<<1|1,L,R,t);
pushup(rt);//和的时候是对的
}
int query(int rt, int L, int R){//询问就要下放
// cout<<L<<" "<<R<<" "<<tree[rt].sum<<endl;
if(L <= tree[rt].l && R >= tree[rt].r){
return tree[rt].sum;//err:sum在update已经算过了
}
if(tree[rt].one != -1) pushdown(rt);
int mid = (tree[rt].l + tree[rt].r)>>1;
int sum = 0;
if(L <= mid)
sum += query(rt<<1,L,R);
if(R > mid)
sum += query(rt<<1|1,L,R);
return sum;
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n-1; i++){
scanf("%d",&x);
add(x,i);
}
dfs1(0);
tp[0] = 0; dfs2(0);
build(1,1,n);
scanf("%d",&m);
for(int i = 1; i <= m; i++){
scanf("%s%d",str,&x);
int sum = 0;
if(str[0] == 'i'){
while(tp[0] != tp[x]){
sum += query(1,id[tp[x]],id[x]);
update(1,id[tp[x]],id[x],0);
x = fa[tp[x]];
}
sum += query(1,id[0],id[x]);
printf("%d\n",sum);
update(1,id[0],id[x],0);
// for(int i = 1; i <= 13; i++)
// cout<<i<<" "<<tree[i].one<<endl;
}else if(str[0]=='u'){//卸载就是对子树进行操作,在序列上一定是个子段
sum = size[x] - query(1,id[x],id[x]+size[x]-1);
printf("%d\n",sum);
update(1,id[x],id[x]+size[x]-1,1);
}
}
return 0;
}
/*
9
0 1 2 0 1 5 2 5
1
install 3
*/
这里少了一个加号,惨不忍睹。
3. 使用数链剖分求lca
5 3 1 2 3 1 3 4 5 3 2 3 -> 1 1 5 -> 1 3 3 -> 3
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> using namespace std; int n,m,dep[100005],f[100005],size[100005],cnt,hd[100005],son[100005],tp[100005]; struct Edge{ int nxt, to; }edge[200005]; void add(int u, int v){ cnt++; edge[cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void dfs1(int u, int fa){ int mx = -1; size[u] = 1; for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dep[v] = dep[u] + 1; f[v] = u; dfs1(v, u); size[u] += size[v]; if(size[v] > mx){ mx = size[v], son[u] = v; } } } void dfs2(int u, int top, int fa){ tp[u] = top; if(son[u]) dfs2(son[u], tp[u], u); for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; if(v != son[u]) dfs2(v, v, u); } } int LCA(int x, int y){ while(tp[x] != tp[y]){ if(dep[tp[x]] < dep[tp[y]]) swap(x,y); x = f[tp[x]]; } if(dep[x] < dep[y]) return x; else return y; } int main(){ int x,y,z; scanf("%d%d",&n,&m); for(int i = 1; i <= n-1; i++){ scanf("%d%d",&x,&y); add(x,y); add(y,x); } dep[1] = 1; dfs1(1,0); dfs2(1,1,1); for(int i = 1; i <= m; i++){ scanf("%d%d%d",&x,&y); } return 0; }
二刷
#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #define N 300005 using namespace std; int n, m, x, y, siz[N], top[N], hd[N], cnt, dep[N], son[N], f[N]; struct Edge{ int nxt, to; }edge[N*2]; void add(int u, int v){ edge[++cnt].to = v; edge[cnt].nxt = hd[u]; hd[u] = cnt; } void dfs1(int u, int fa){ f[u] = fa; siz[u] = 1; dep[u] = dep[fa] + 1; for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; if(v == fa) continue; dfs1(v, u); siz[u] += siz[v]; if(siz[v] > siz[son[u]]) son[u] = v; } } void dfs2(int u, int fa, int tp){ top[u] = tp; if(son[u]) dfs2(son[u], u, tp); for(int i = hd[u]; i; i = edge[i].nxt){ int v = edge[i].to; //nnd,写成edge[i].nxt if(v == fa || v == son[u]) continue; dfs2(v, u, v); } } int lca(int x, int y){ while(top[x] != top[y]){ if(dep[top[x]] < dep[top[y]]) swap(x,y); x = f[top[x]]; } return dep[x] < dep[y] ? x:y;//error dep,top搞混 } int main(){ scanf("%d%d",&n,&m); for(int i = 1; i <= n-1; i++){ scanf("%d%d",&x,&y); add(x,y); add(y,x); } dfs1(1,0); // for(int i = 1; i <= n; i++) // cout<<"son: "<<i<<" "<<son[i]<<endl; dfs2(1,0,1); // for(int i = 1; i <= n; i++) // cout<<i<<" "<<f[i]<<" "<<siz[i]<<" "<<dep[i]<<endl; // cout<<"hhh: "<<i<<" "<<top[i]<<endl; for(int i = 1;i <= m; i++){ scanf("%d%d",&x,&y); printf("%d\n",lca(x,y)); } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号