Jeanny
寂兮,寥兮,独立不改,周行而不殆
区间dp

 

[NOI1995]石子合并

#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x7fffffff
using namespace std;
long long n,a[1005],f[1005][1005],sm[1005],s[1005][1005],ans1=INF,ans2=-INF;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);//可以不写成数组形式 
        sm[i]=sm[i-1]+a[i];
    }
    for(int i=n+1;i<=2*n-1;i++)
    {
        a[i]=a[i-n];
        sm[i]=sm[i-1]+a[i];
    }
//    memset(f,1,sizeof f);
//    for(int i=1;i<=2*n-1;i++) f[i][i]=0;
    for(int t=2;t<=2*n-1;t++)//区间 
    {
        for(int i=1;i<=2*n-1;i++)//起点 
        {
            
            int j=i+t-1;//终点
            f[i][j]=INF;
            if(j<=2*n-1)
                for(int k=i;k<=i+t-2;k++)//下面有个k+1 
                {
                    f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sm[j]-sm[i-1]); 
                }
        }
    }
    for(int i=1;i<=2*n-1;i++)
        ans1=min(ans1,f[i][i+n-1]);
    cout<<ans1<<endl;
    

    for(int t=2;t<=2*n-1;t++)//区间 
    {
        for(int i=1;i<=2*n-1;i++)//起点 
        {    
            int j=i+t-1;//终点 
            f[i][j]=-INF;
            if(j<=2*n-1)
                for(int k=i;k<=i+t-2;k++)//下面有个k+1 
                {
                    f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+sm[j]-sm[i-1]); 
                }
        }
    }
    for(int i=1;i<=2*n-1;i++)
        ans2=max(ans2,f[i][i+n-1]);
    cout<<ans2<<endl;//开始写成了cout<<f[1][2*n-1] 
}

 

P1063 能量项链 

2 3 5 10 2 3 5 10
   i     k   j
f[i][j] 表示第i个珠子到第j的珠子能释放的最大能量,且用珠子的头标记去表达

f[i][j] = f[i][k] + f[k+1][j] + a[i][k+1][j]
如果前一颗能量珠的头标记为m，尾标记为r，后一颗能量珠的头标记为r，尾标记为n，
则聚合后释放的能量为m×r×n .

 

 

P1220 关路灯

f[i][j]表示从地址i到地址j关路灯的最小值，关灯一定是连续的，因此这个区间最后一个位置是在左边还是右边，可以多一维数组来表示状态。

答案一定是f[i][j][0],f[i][j][1]中最小的。

f[i][j][0] = min( f[i+1][j][0] + (a[i+1] - a[i]) * p[i] , f[i+1][j][1] + (a[j] - a[i]) * p[i]); 
f[i][j][1] = min( f[i][j-1][1] + (a[j] - a[j-1]) * p[j] , f[i][j-1][0] + (a[j] - a[i]) * p[j] );

纠结的地方在于已经写出来状态转移方程式了，但是并不清楚如何写循环顺序。其实还是按照区间dp的套路去写。

这里状态转移方程中的p[i]是不正确的，因为再上一个灯关完到当前灯关完的这段时间，其余亮着的灯都在等。因此更新为sp[n]-sp[j] + sp[i] ,下面也是一样。

f[i][j][0] = min( f[i+1][j][0] + (a[i+1] - a[i]) * (sp[n]-sp[j] + sp[i]) , f[i+1][j][1] + (a[j] - a[i]) * (sp[n]-sp[j] + sp[i]) ); 
f[i][j][1] = min( f[i][j-1][1] + (a[j] - a[j-1]) * (sp[n]-sp[j-1] + sp[i-1]) , f[i][j-1][0] + (a[j] - a[i]) * (sp[n]-sp[j-1] + sp[i-1]) );//这里一开始写成和上面一样了

 完整代码：

#include<bits/stdc++.h>
using namespace std;
int n,c,a[55],p,sp[55],f[55][55][2];
 
int main(){
    scanf("%d%d",&n,&c);
    for(int i = 1; i <= n; i++){
        scanf("%d%d",&a[i],&p);
        sp[i] = sp[i-1] + p;
    }
    memset(f,0x3f,sizeof f);
    f[c][c][0] = f[c][c][0] = 0;
    for(int k = 2; k <= n; k++)
        for(int i = 1; i + k - 1 <= n; i++){
            int j = i + k - 1;
                f[i][j][0] = min( f[i+1][j][0] + (a[i+1] - a[i]) * (sp[n]-sp[j] + sp[i]) , f[i+1][j][1] + (a[j] - a[i]) * (sp[n]-sp[j] + sp[i]) );
                f[i][j][1] = min( f[i][j-1][1] + (a[j] - a[j-1]) * (sp[n]-sp[j-1] + sp[i-1]) , f[i][j-1][0] + (a[j] - a[i]) * (sp[n]-sp[j-1] + sp[i-1]) );
         }
    printf("%d\n",f[1][n][0] < f[1][n][1] ? f[1][n][0]:f[1][n][1]);
    return 0;
}


P3205 [HNOI2010]合唱队

1. 上一个队形有几种方案，那么当前这个人站在左边（或者右边），就有多少方案。

2. 我们用f[i][j]表示从i的人到j的人排队的方案数，那么f[i][j]和f[i+1][j]、f[i][j-1]有什么关系，但是并不知道是和左边的去比还是右边的，因此考虑到转移的方式是f[i][j] = f[i+1][j]的前提是a[i]小于最后一个数，那如果最后一个数是在左边和右边，是不同的状态，因此考虑多一维,表示最后一个数字放左边还是右边。

if(a[i] < a[i+1]) f[i][j][0] += f[i+1][j][0] 

if(a[i] > a[i+1]) f[i][j][1] += f[i][j-1][0] 

... ...

考虑一个数字的时候，两个数字的时候，因此需要有一个步长，将1、2....n步长求出来，其余的和其他区间dp一样。

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
const int maxn=1000+7,mod=19650827;
static int dp[maxn][maxn][2],n,a[maxn];
int main(){
  scanf("%d",&n);
  for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
  for(int i = 1; i <= n; i++) dp[i][i][0]=1;
  for(int t=2;t<=n;t++)
    {
      for(int i=1;i<=n;i++)
      {
          int j=i+t-1;
          if(j>n) break;
          if(a[j]>a[j-1]) dp[i][j][1]+=dp[i][j-1][1];
          if(a[j]>a[i]) dp[i][j][1]+=dp[i][j-1][0];
          if(a[i]<a[i+1]) dp[i][j][0]+=dp[i+1][j][0];
          if(a[i]<a[j]) dp[i][j][0]+=dp[i+1][j][1];
          dp[i][j][0]%=mod;
          dp[i][j][1]%=mod;
      }
    }
    printf("%d",(dp[1][n][0]+dp[1][n][1])%mod);    
}

 

P4170 [CQOI2007]涂色

1. 状态
    因为是区间DP，所以状态很好设：
    设 f[i][j]为区间 [i,j]修改为目标状态的最少次数。

2. 初始化

    因为因为 长度为 1 的区间肯定只需涂了一次颜色，所以： f[i][i]=1;
    因为求的是区间涂色最少次数，所以 任意 f[i][j] 取无穷大 ，这个应该很好理解。

3. 状态转移

    解决区间类DP问题，一般需要考虑其跟 i 相邻的位置或跟 j 相邻的位置的状态之间的关系。

    这里有一点 floyd 求全源最短路的思想，通过不断找 中转点 k ，更新 f[i][j]的值，即 :

    f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);

    所以状态转移方程如下:

        当 a[i]==a[j]时（首尾两个格子可以一次涂掉 ） :

        f[i][j]=min(f[i+1][j],f[i][j−1]);

        当 a[i]!=a[j] 时（大多数区间DP更新值的写法） :

        f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);

4. 答案

    显然，是 f[1][n] 。

#include<bits/stdc++.h>
using namespace std;
char s[55];
int color[55];
int f[55][55];
int main(){
    scanf("%s",s+1);
    int n = strlen(s+1);
    for(int i=1;i<=n;i++) color[i]=s[i]-'A'+1;
    memset(f,0x3f,sizeof f);
    for(int i = 1; i <= n; i++) f[i][i]=1;
    for(int len = 2; len <= n; len++){
        for(int i = 1; i+len-1 <= n; i++){
            int j = i+len-1;
            if(color[i] == color[j])
                f[i][j] = min(f[i][j], min(f[i+1][j-1]+1, min(f[i][j-1],f[i+1][j])));
            else {
                for(int k = i; k < j; k++)
                    f[i][j] = min(f[i][j], f[i][k] + f[k+1][j]);
            }
        }
    }
    printf("%d\n",f[1][n]);
}

 

P3146 [USACO16OPEN]248 G

给定一个1*n的地图，在里面玩2048，每次可以合并相邻两个（数值范围1-40），问最大能合出多少。注意合并后的数值并非加倍而是+1，例如2与2合并后的数值为3。

input:    output: 3
4 
1
1
1
2

设计状态：f[i][j] 表示完全合并的最大数字，也就是石子合并的原版。
状态转移方程：f[i][j] = max(f[i][j], f[i][k] + 1) (f[i][k] == f[k+1][j])
            ans = max(ans, f[i][j]);
一开始想成f[i][j]表示从i到j区间可以合并的最大值，那么答案是f[1][n].错误原因是对于不相邻的相同数字，是无法完成合并的，因此无法转移。比如：4 1 4， 4、1和4两个区间。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n, dp[300][300], ans;
signed main(){
    scanf("%lld",&n);
    for(int i = 1; i <= n; i++){
        scanf("%lld",&dp[i][i]);
    }
    for(int l = 2; l <= n; l++){
        for(int i = 1; i + l - 1 <= n; i++){
            int j = i + l - 1;
            for(int k = i; k + 1 <= j; k++){
                if(dp[i][k] == dp[k+1][j])
                    dp[i][j] = max(dp[i][j], dp[i][k] + 1); 
                    ans = max(ans, dp[i][j]);
            }
            
        }    
    }
    printf("%lld\n", ans);
    return 0;
}

 

P4342 [IOI1998]Polygon

https://www.luogu.com.cn/problem/P4342

1.如何处理这样一个环。

2.如何得到最开始删除的边。

对于第一个问题，很轻易地就可以想到断环成链，同时我们还可以发现，通过断环成链，我们把第二个问题就解决了，我们可以通过对最后的结果再来一次对最大值的遍历，输出即可。

开始考虑DPDP，首先我们可以很显然的得到一个区间DPDP的板子：

设f[i][j]f[i][j]表示[i,j][i,j]这一个区间内可以得到的最大得分，转移方程如下：

加法：f[i][j]=max(f[i][k]+f[k+1][j])

乘法：f[i][j]=max(f[i][k]×f[k+1][j])

但是深入去想，乘法最大，可能是两个负数相乘的结果，因此要维护最小值。最小值可能是最小*最小，最大*最大（负数），最大*最小，最小*最大（一正一负）。

乘法最大，可能是最大*最大（正），最小*最小（负数），最大*最小（负*正），最小*最大（正*负）

https://www.luogu.com.cn/problem/solution/P4342?page=1 第一篇题解代码

 

CF607B Zuma

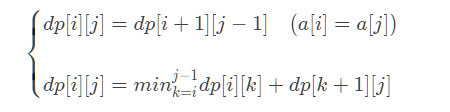
#include<bits/stdc++.h>
using namespace std;
const int N=505;
const int inf=233333333;

int n,a[N],dp[N][N];

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    for (int i=1;i<=n;i++)
    for (int j=1;j<=n;j++) dp[i][j]=inf;  //开始全赋inf，否则转移取min时就会挂掉
    for (int i=1;i<=n;i++) dp[i][i]=1;  //直接取一个数，花费一个代价
    for (int i=1;i<n;i++) dp[i][i+1]=1+(a[i]!=a[i+1]);  //取两个数的情况，如果相等取一次就好了，否则取两次
    for (int i=3;i<=n;i++)  //注意转移时需要先枚举区间长度
    for (int j=1;i+j-1<=n;j++)
    {
        int l=j,r=i+j-1;  //计算区间左右端点
        if (a[l]==a[r]) dp[l][r]=dp[l+1][r-1];
        for (int k=l;k<r;k++) dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]);  //转移
    }
    printf("%d",dp[1][n]);

    return 0;
}

hdu6212祖玛游戏 区间dp

课课通，数字游戏

#include<bits/stdc++.h>#define int long longusing namespace std;int n, dp[300][300], ans;signed main(){scanf("%lld",&n);for(int i = 1; i <= n; i++){scanf("%lld",&dp[i][i]);}for(int l = 2; l <= n; l++){for(int i = 1; i + l - 1 <= n; i++){int j = i + l - 1;for(int k = i; k + 1 <= j; k++){if(dp[i][k] == dp[k+1][j])dp[i][j] = max(dp[i][j], dp[i][k] + 1); ans = max(ans, dp[i][j]);}}}printf("%lld\n", ans);return 0;} 
posted on 2020-06-06 09:59  Jeanny  阅读(254)  评论(0)    收藏  举报

博客园  ©  2004-2025
浙公网安备 33010602011771号 浙ICP备2021040463号-3 Powered By博客园