贪心算法

贪心算法,在我看来就是题做多了,就能够找到了一种最优秀的做法。但其实也没什么，这里举例几个问题。

1.拼接字符串形成最小字典序

这是一道贪心的问题,而它主要是点就在于不同字符串的排序规则,它排序的规则是string1.string2跟string2.string1,两者拼接之后的大小来排序.

所以这里只需要写一个比较器,然后从头拼接到尾即可

"abc"与"bce"长度一样,以ASCAII值对比,
"abc"与"b"长度不一样时,补上"0",即"abc"与"b00".
但在排序时,比如"b"与"ba",虽然"ba"比"b"大,但是拼接起来,"bab"比"bba"小

public class LowestLexicography {
    public static class MyComparator implements Comparator<String>{

        @Override
        public int compare(String o1, String o2) {
            return (o1+o2).compareTo(o2+o1);
        }
    }
    public static String lowestString(String[] strs){
        if(strs == null || strs.length == 0){
            return "";
        }
        Arrays.sort(strs, new MyComparator());
        String resString = "";
        for (String string : strs) {
            resString += string;
        }
        return resString;
    }

}

2.金条切割费用最低问题

给定一个数值为金条的长度，和一个int数组表示需要把金条切割成不同的长度，切割的费用为切割的金条长度，求切割费用最小为多少。

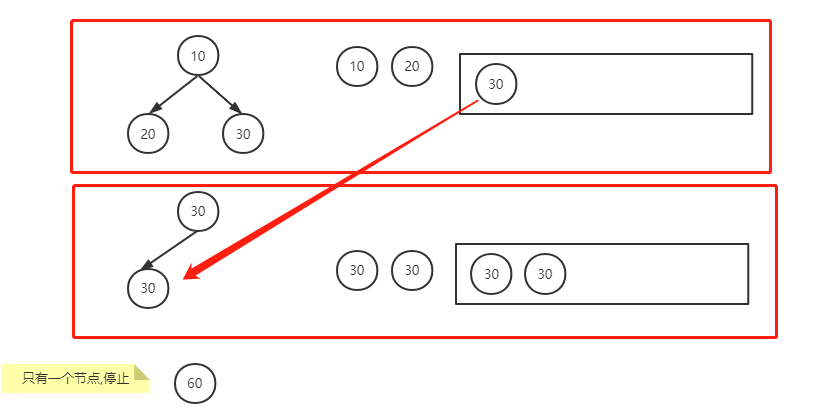
60 int[] = [10,20,30]

这也是一道贪心问题,但是用到了哈夫曼编码,我们把数组丢进一个小根堆里面,然后每次把小根堆里面的最小的两个数拿出来,相加为切割的费用,再把切割费用丢进小根堆,直到小根堆只有一个节点停止,累计的费用为所求的最低费用.

 

public static int lessMoney(int[] arr) {
        PriorityQueue<Integer> pQ = new PriorityQueue<>();
        for (int i = 0; i < arr.length; i++) {
            pQ.add(arr[i]);
        }
        int sum = 0;
        int cur = 0;
        while (pQ.size() > 1) {
            cur = pQ.poll() + pQ.poll();
            sum += cur;
            pQ.add(cur);
        }
        return sum;
    }

    public static class MinheapComparator implements Comparator<Integer> {

        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2; // < 0  o1 < o2  负数
        }

    }

    public static class MaxheapComparator implements Comparator<Integer> {

        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1; // <   o2 < o1
        }

    }

 3.举办最多宣讲会

 

public static class Node {
        public int p;
        public int c;

        public Node(int p, int c) {
            this.p = p;
            this.c = c;
        }
    }

    public static class MinCostComparator implements Comparator<Node> {

        @Override
        public int compare(Node o1, Node o2) {
            return o1.c - o2.c;
        }

    }

    public static class MaxProfitComparator implements Comparator<Node> {

        @Override
        public int compare(Node o1, Node o2) {
            return o2.p - o1.p;
        }

    }

    public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {
        Node[] nodes = new Node[Profits.length];
        for (int i = 0; i < Profits.length; i++) {
            nodes[i] = new Node(Profits[i], Capital[i]);
        }

        PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());
        PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
        for (int i = 0; i < nodes.length; i++) {
            minCostQ.add(nodes[i]);
        }
        for (int i = 0; i < k; i++) {
            while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {
                maxProfitQ.add(minCostQ.poll());
            }
            if (maxProfitQ.isEmpty()) {
                return W;
            }
            W += maxProfitQ.poll().p;
        }
        return W;
    }